完美矩阵

目录

• 题目
• 思路
• 代码

题目

思路

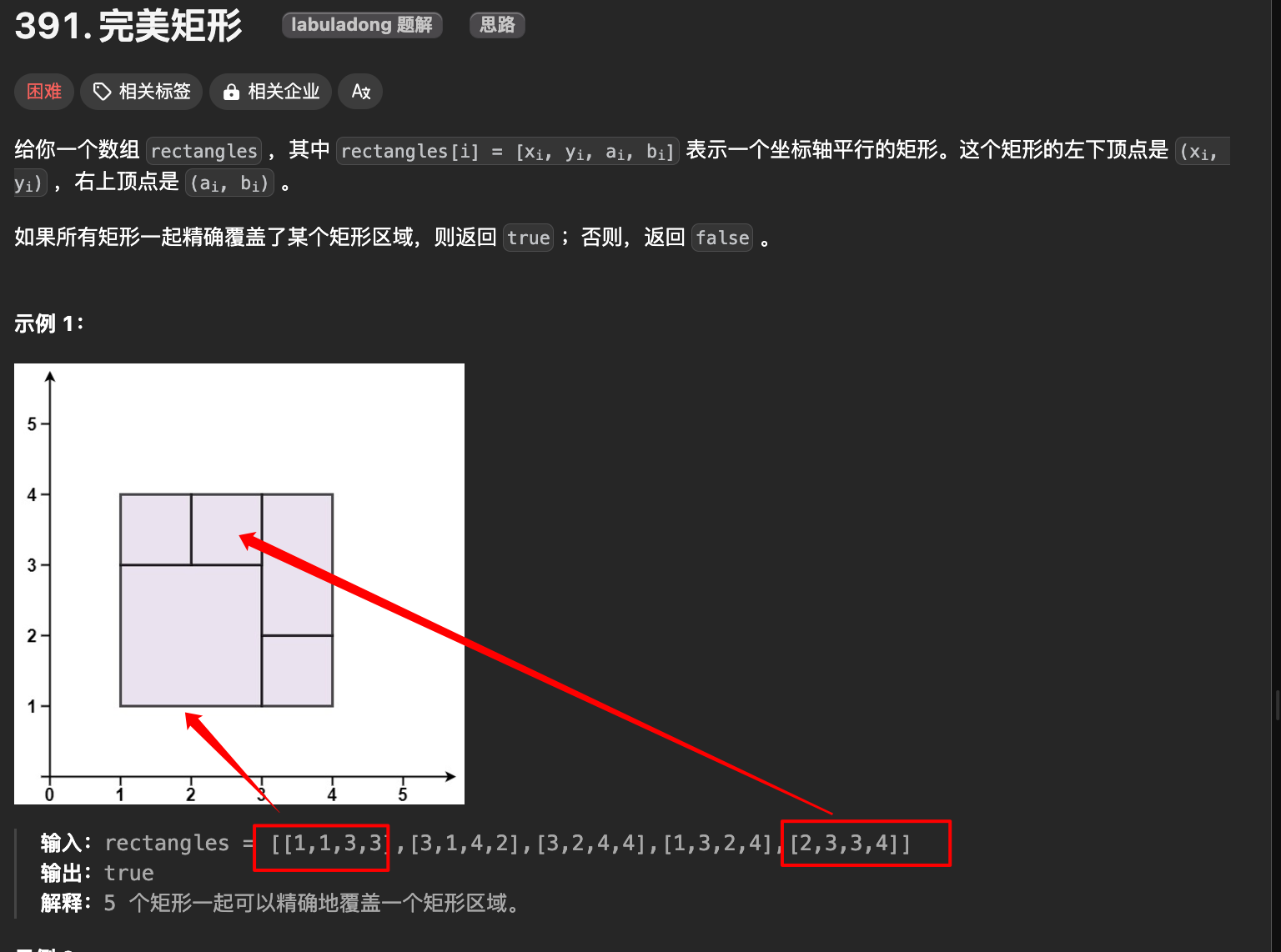
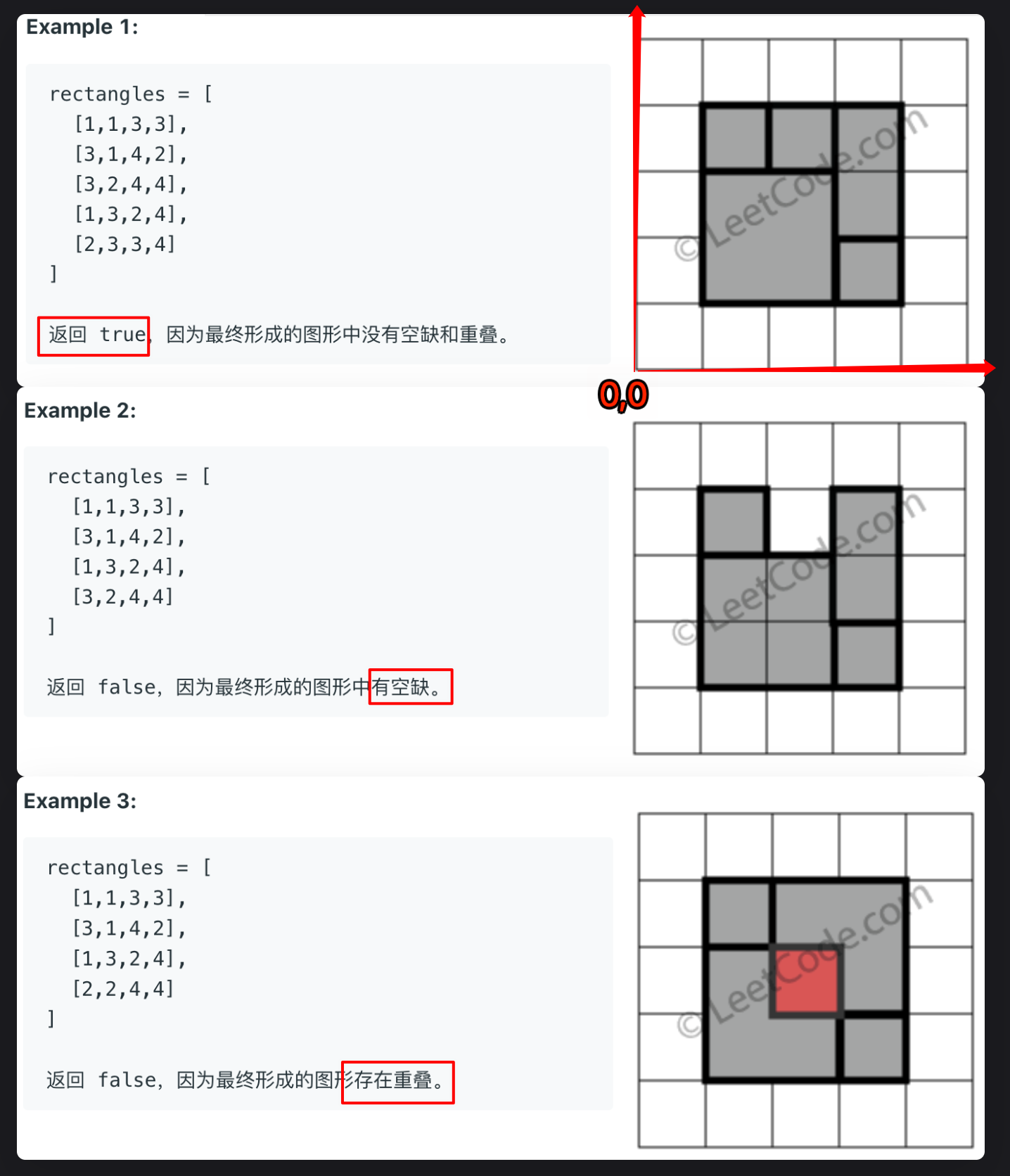
1. 判断面积，通过完美矩形的理论坐标计算出一个理论面积，然后和 rectangles 中小矩形的实际面积和做对比
2. 判断顶点，points 集合中应该只剩下 4 个顶点且剩下的顶点必须都是完美矩形的理论顶点

代码

var isRectangleCover = function(rectangles) {
    var X1 = Number.MAX_VALUE, Y1 = Number.MAX_VALUE;
    var X2 = Number.MIN_VALUE, Y2 = Number.MIN_VALUE;
    var actualArea = 0;
    // 哈希集合，记录最终图形的顶点
    var points = new Set();
    for (var rect of rectangles) {
        var x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        X1 = Math.min(X1, x1);
        Y1 = Math.min(Y1, y1);
        X2 = Math.max(X2, x2);
        Y2 = Math.max(Y2, y2);
        actualArea += (x2 - x1) * (y2 - y1);
        // 先算出小矩形每个点的坐标，用字符串表示，方便存入哈希集合
        var p1 = x1 + "," + y1;
        var p2 = x1 + "," + y2;
        var p3 = x2 + "," + y1;
        var p4 = x2 + "," + y2;
        // 对于每个点，如果存在集合中，删除它；
        // 如果不存在集合中，添加它；
        // 这个简单的逻辑，让 `points` 集合最终只会留下那些出现了 1 次或者 3 次的顶点，
        // 那些出现了 2 次或者 4 次的顶点都被消掉了
        // 在集合中剩下的点都是出现奇数次的点
        for (var p of [p1, p2, p3, p4]) {
            if (points.has(p)) {
                points.delete(p);
            } else {
                points.add(p);
            }
        }
    }
    var expectedArea = (X2 - X1) * (Y2 - Y1);
    if (actualArea != expectedArea) {
        return false;
    }
    // 检查顶点个数
    if (points.size != 4 || 
        !points.has(X1 + "," + Y1) || 
        !points.has(X1 + "," + Y2) || 
        !points.has(X2 + "," + Y1) || 
        !points.has(X2 + "," + Y2)) {
        return false;
    }
    return true;
};