路径总和 III

#leetcode #2024/08/17 #算法/二叉树 #算法/前缀和

目录

• 1. 题目及理解
• 2. 解题思路
• 3. 代码实现
• 4. 复杂度分析
• 5. 错误记录

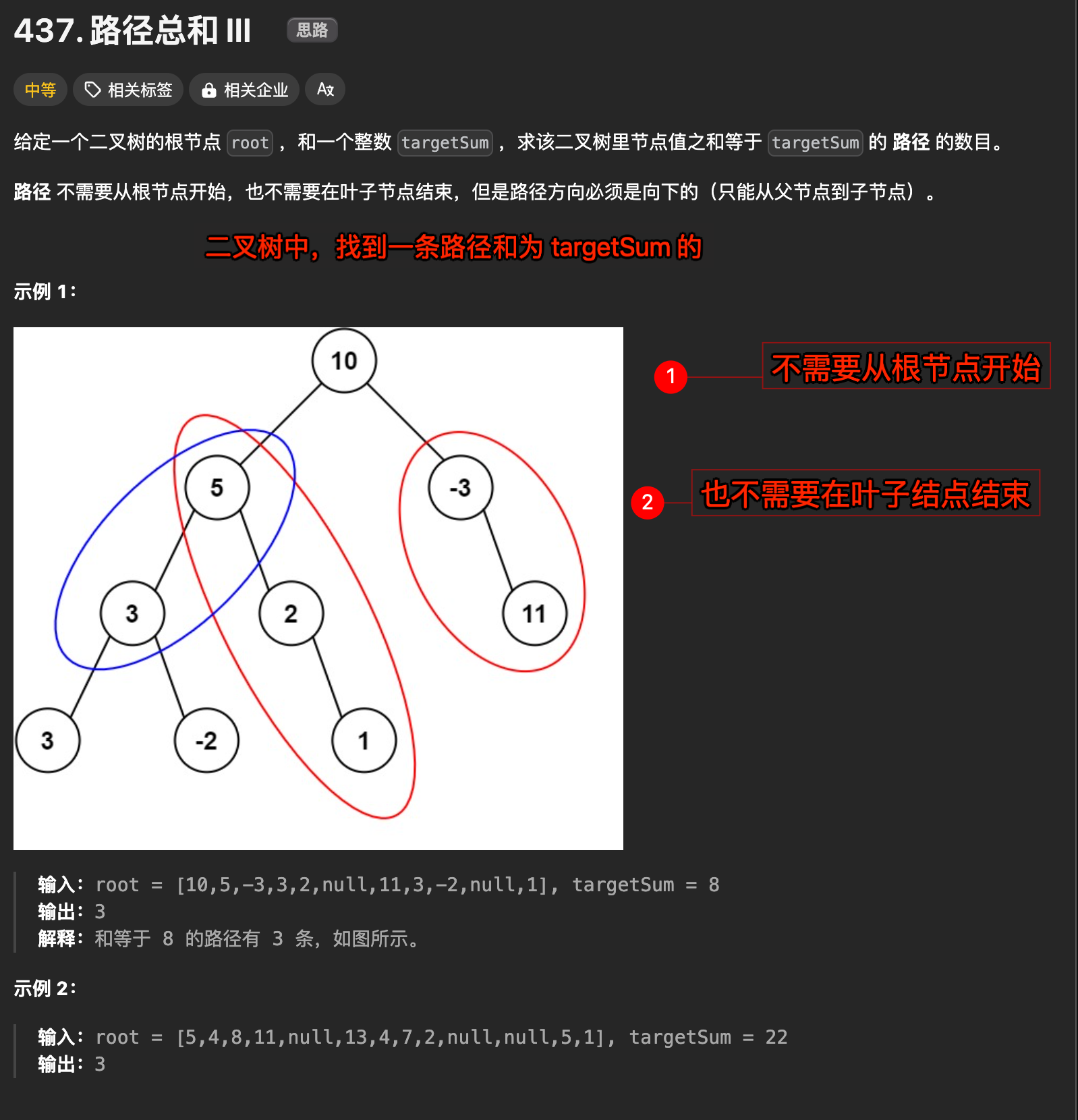
1. 题目及理解

2. 解题思路

• 二叉树的前序后序遍历
• 前缀和技巧

3. 代码实现

/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {

    // key 是前缀和，value 是前缀和为 pathSum 的个数
    const preSumCount = new Map();
    // 初始化，前缀和为 0 的路径有一条
    // 为什么要初始化呢？
    // 这个设置可以被理解为代表一个"空路径"，其和为 0
    preSumCount.set(0, 1);
    // pathSum 记录当前路径和，即从根节点到当前节点的路径和
    let pathSum = 0;
    // res 记录满足条件的路径条数
    let res = 0;
    const traverse = function(root) {
        // 递归终止条件
        // base case
        if (root == null) {
            return;
        }
        /*************************************************
         * ::::::::::::::::::::: 前序遍历位置 ::::::::::::::::::
         ************************************************/
        // 前序遍历位置, 计算路径和
        pathSum += root.val;

        // 先看一下路径和为 pathSum - targetSum 的路径有多少条
        // :::: pathSum - targetSum 代表的是从根节点到当前节点的路径和为 targetSum
        // 即满足条件的路径，所以更新 res 的值
        res += preSumCount.get(pathSum - targetSum) || 0;
        // 记录从二叉树的根节点开始，路径和为 pathSum 的路径条数
        preSumCount.set(pathSum, (preSumCount.get(pathSum) || 0) + 1);
        traverse(root.left);
        traverse(root.right);
        /*************************************************
         * ::::::::::::::: 后序遍历位置 ::::::::::::::
         ************************************************/
        preSumCount.set(pathSum, preSumCount.get(pathSum) - 1);
        pathSum -= root.val;
    }

    traverse(root);
    return res;
};

4. 复杂度分析

• 时间复杂度：O(N)，其中 N 是树中的节点数。
• 空间复杂度：O(N)，主要由递归调用栈和 preSumCount Map 贡献。

5. 错误记录

初始化空路径的处理：preSumCount.set(0, 1);