二叉树着色游戏

1145. 二叉树着色游戏

目录

1. 总结

1.1. 关键思路

  • 玩家2 要想获胜，必须能够控制比总节点数一半还多的节点
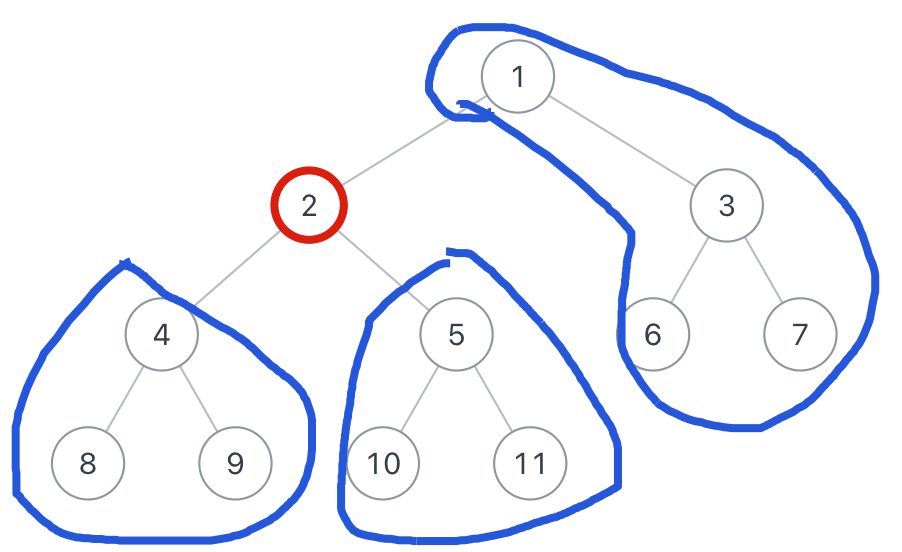
  • 玩家2 的第一步选择非常关键，需要选择一个可以切断玩家 1 扩展路径的位置
  • 实际上就是在找：在玩家1选择 x 后，x 的左子树、右子树、以及父节点方向，哪个部分的节点数最多

这样理解后，这道题就从一个博弈问题转化成了一个计算问题：

  1. 找到节点 x
  2. 计算它把树分成的三个部分各自的节点数
  3. 判断最大的那部分是否超过 n/2

图片&文件

var btreeGameWinningMove = function (root, n, x) {
    // 定义：在以 root 为根的二叉树中搜索值为 x 的节点并返回
    function find(root, x) {
        if (!root) return null;
        if (root.val === x) return root;
        let left = find(root.left, x);
        if (left) return left;
        return find(root.right, x);
    }

    // 定义：计算以 root 为根的二叉树的节点总数
    function count(root) {
        if (!root) return 0;
        return 1 + count(root.left) + count(root.right);
    }

    let node = find(root, x);
    let leftCount = count(node.left);
    let rightCount = count(node.right);
    let otherCount = n - leftCount - rightCount - 1;
    return (
        Math.max(leftCount, Math.max(rightCount, otherCount)) >
        Math.floor(n / 2)
    );
};

2. 题目

2.1. 游戏规则

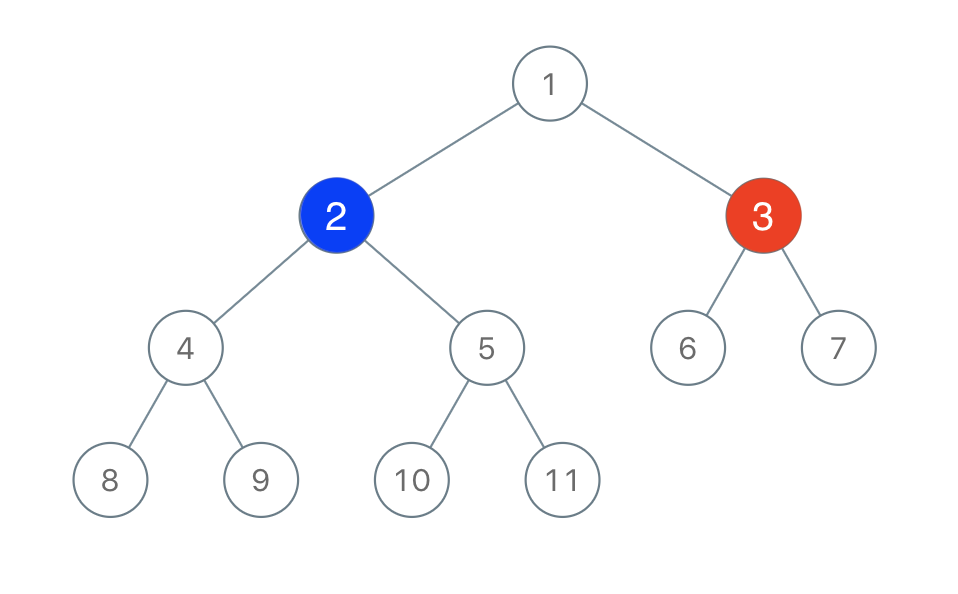
  1. 有两个玩家：
    • 玩家 1（蓝色）
    • 玩家 2（红色）
  2. 游戏过程：
    • 玩家 1 先手，选择一个节点染成蓝色
    • 玩家 2 后手，选择一个未着色的节点染成红色
    • 之后两人轮流操作，每次只能选择未着色的节点
  3. 关键规则：
    • 每个玩家只能选择与自己已经染色节点相邻的节点
    • “相邻” 意味着两个节点之间有一条边直接相连
  4. 胜利条件：
    • 谁能染色更多的节点，谁就赢

图片&文件

2.2. 题目输入

  • 一棵二叉树
  • 整数 n（节点总数）
  • 整数 x（玩家1 选择的第一个节点）

2.3. 具体例子

例如这样一棵树：
     1
    / \
   2   3
  / \  /
 4   5 6

n = 6, x = 3

假设玩家1选择了节点3（题目给定的x值）：

     1
    / \
   2   [3蓝]
  / \  /
 4   5 6

现在轮到玩家2选择。玩家2可以选择的节点必须和蓝色节点（3）相邻。 在这个例子中，玩家2可以选择的节点有：

  • 节点1（3的父节点）
  • 节点6（3的子节点）

如果玩家2选择节点1：

     [1红]
    / \
   2   [3蓝]
  / \  /
 4   5 6

这样玩家2就可以后续染色2,4,5节点，而玩家1只能染色节点6。 最终结果：玩家2可以获得4个节点（1,2,4,5），玩家1只能获得2个节点（3,6）。 所以玩家2可以获胜。

2.4. 问题转化

实际上，这个问题可以转化为：

  1. 玩家1已经选择了节点 x
  2. 这个选择会把整棵树分成三个部分：
    • 选中节点 x 的左子树
    • 选中节点 x 的右子树
    • 选中节点 x 的父节点及其相连的其他部分
  3. 玩家2只要能选择一个位置，使得他能控制这三个部分中最大的那个，就可以赢

图片&文件