统计二叉树中好节点的数目：

#leetcode #算法/二叉树

目录

• 1. 总结
• 2. 题目及理解
  • 2.1. 好节点定义
• 3. 解题思路：遍历一遍二叉树的思路
• 4. 复杂度分析
• 5. 注意点

1. 总结

• 关键点：
  • max 变量，遍历到一个节点就更新节点
    • 注意是 max = root.val 而不是 max = max + 1
      • 刷太多题了吧，这都搞错

var goodNodes = function (root) {
  if (!root) return 0;
  let res = 0;
  function traverse(root, max) {
    if (!root) return;
    if (root.val >= max) {
      res++;
      max = root.val;
    }
    traverse(root.left, max);
    traverse(root.right, max);
  }
  traverse(root, root.val);
  return res;
};

2. 题目及理解

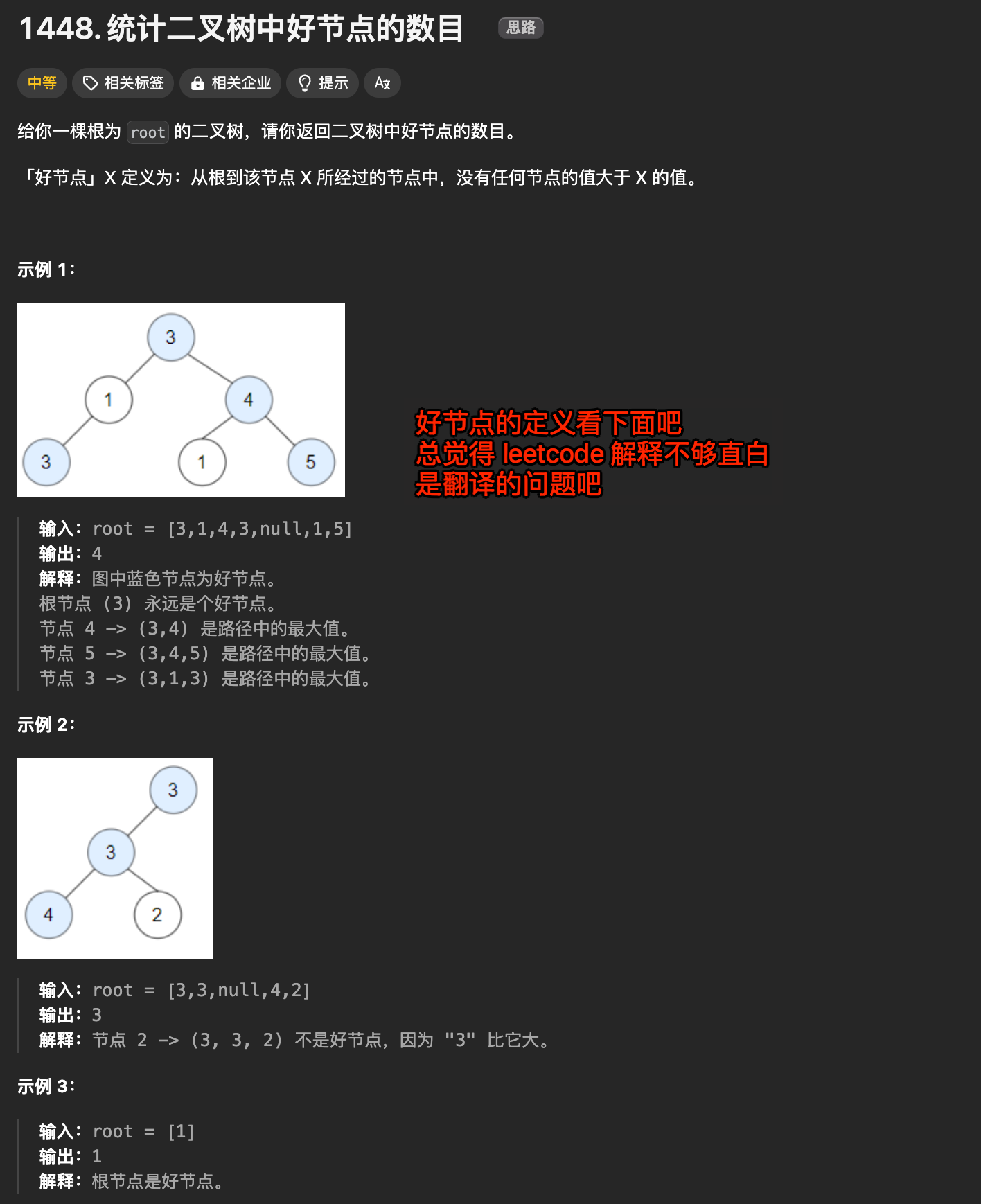
2.1. 好节点定义

如果从根节点到这个节点的路径上的所有节点值都不大于这个节点的值，那么这个节点被称为“好节点“。

举个例子：

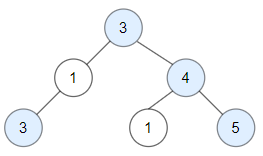
这个树的结构是：

• 根节点是 3
• 左子节点是 1
  • 左子节点是 3
• 右子节点是 4
  • 左子节点是 1
  • 右子节点是 5

现在，让我们再次分析这个树中的 “好节点” ：

1. 根节点 3 是好节点（路径上只有它自己）
2. 左子树的 1 不是好节点（因为 3 > 1）
3. 左子树的 3 是好节点（因为 3 >= 3）
4. 右子树的 4 是好节点（因为 4 > 3）
5. 右子树的 1 不是好节点（因为 3 > 1 且 4 > 1）
6. 右子树的 5 是好节点（因为 5 > 3 且 5 > 4）

因此，这个树中共有 4 个好节点

3. 解题思路：遍历一遍二叉树的思路

/**
 * @param {TreeNode} root
 * @return {number}
 */
var goodNodes = function (root) {
  // 好节点的数量
  let res = 0;
  // 递归函数
  /**
   * @param {TreeNode} node 当前节点
   * @param {number} max 当前路径上的最大值, 初始值为根节点的值,
   *                     后面会不断更新，需要传递给子节点
   * */
  function traverse(node, max) {
    if (!node) {
      return;
    }
    // 前序位置
    // 先判断当前节点是否是好节点
    // 如果是，好节点数量加 1，同时更新 max
    if (node.val >= max) {
      res++;
      max = node.val;
    }
    // 继续递归左右子树
    traverse(node.left, max);
    traverse(node.right, max);
  }
  traverse(root, root.val);
  return res;
};

4. 复杂度分析

• 时间复杂度：O(n)
  • 这里的 n 是树中节点的数量。
  • 函数 traverse 会访问树中的每个节点一次，因此时间复杂度是线性的。
• 空间复杂度：O(h)
  • h 是树的高度。
  • 空间复杂度主要来自递归调用栈。在最坏情况下（树完全不平衡，呈现为一条链），高度可能达到 n，此时空间复杂度为 O(n)。
  • 在平衡树的情况下，高度约为 log(n)，空间复杂度为 O(log n)

5. 注意点

• 更新 max 和 res 是在前序位置上