二叉树的序列化与反序列化
#二叉树的序列化 #二叉树的构造
目录
1. 分析
- 序列化:
- root 转成 字符串
"1,2,#,#,#,#,#,#"的格式
- root 转成 字符串
- 反序列化:
- 即
字符串转成二叉树对象 - 即 ==构造二叉树==
- 即
- 注意点:必须配对,不能序列化使用前序,而反序列化使用后序
- 想想就清楚了
- 加上节点后,其实你就可以把这棵树理解为==满二叉树了==
2. 前序遍历的思路
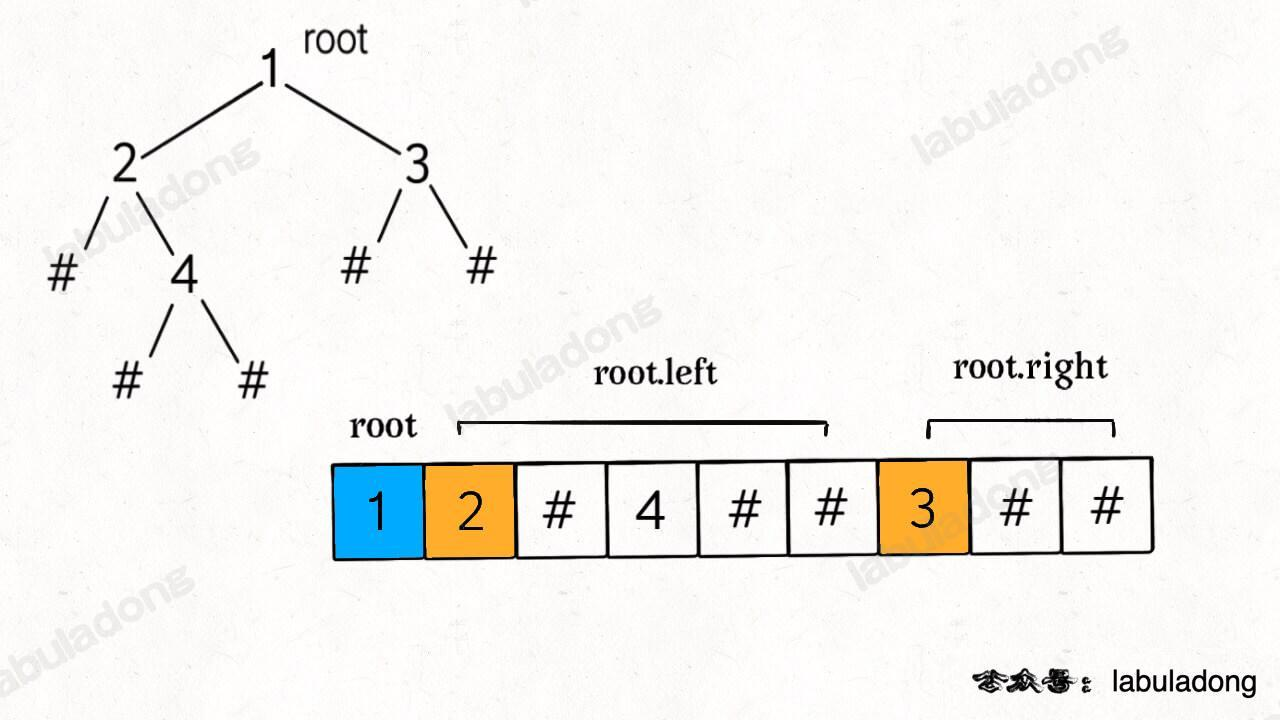
- 序列化:正常前序遍历
- 碰到为空的场景,
push("#")
- 碰到为空的场景,
- 反序列化:
- 即根据前序遍历结果,==还原==一颗二叉树
- 重点:==因为前序遍历结果记录空指针,所以能够唯一还原一个二叉树==
至少要得到前、中、后序遍历中的两种互相配合才能还原二叉树。那是因为前文的遍历结果==没有记录空指针==的信息。 这里的
nodes列表包含了空指针的信息,所以只使用nodes列表就可以还原二叉树
2.1. 序列化
/**
* Encodes a tree to a single string.
*
* @param {TreeNode} root
* @return {string} 比如: "1,2,#,#,4,#,#,#,#";
*/
var serialize = function (root) {
let res = [];
function traverse(root) {
if (!root) {
res.push("#");
return;
}
res.push(root.val);
traverse(root.left);
traverse(root.right);
}
traverse(root);
return res.join(",");
};
2.2. 反序列
/**
* Decodes your encoded data to tree.
*
* @param {string} data 字符串
* @return {TreeNode} "1,2,#,#,#,#,#,#" → 转成 node 节点,本质上就是构造一颗二叉树
*/
var deserialize = function (data) {
console.log("data:", data);
let arr = data.split(",");
return build(arr);
function build(arr) {
if (arr.length === 0) return null;
let first = arr.shift();
if (first === "#") return null;
let root = new TreeNode(parseInt(first));
root.left = build(arr);
root.right = build(arr);
return root;
}
};
3. 中序遍历的思路
- 序列化可以,换个位置而已
- 但无法实现反序列化
4. 后序遍历的思路
- 序列化可以,换个位置而已
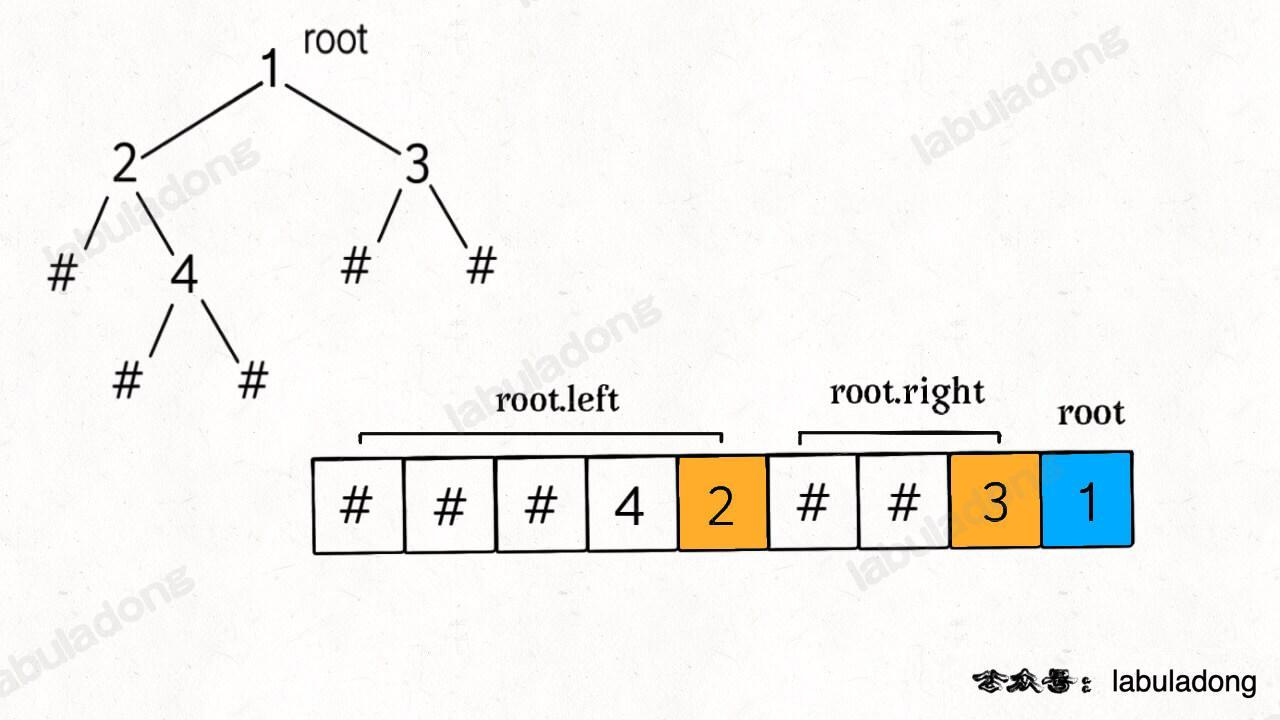
- 反序列,如下图,一样的思路,
- ==根据后序遍历结果(包括空指针)构造一颗二叉树==
- 只不过,每次取值时,
pop即可,不是shift
层次遍历思路
序列化
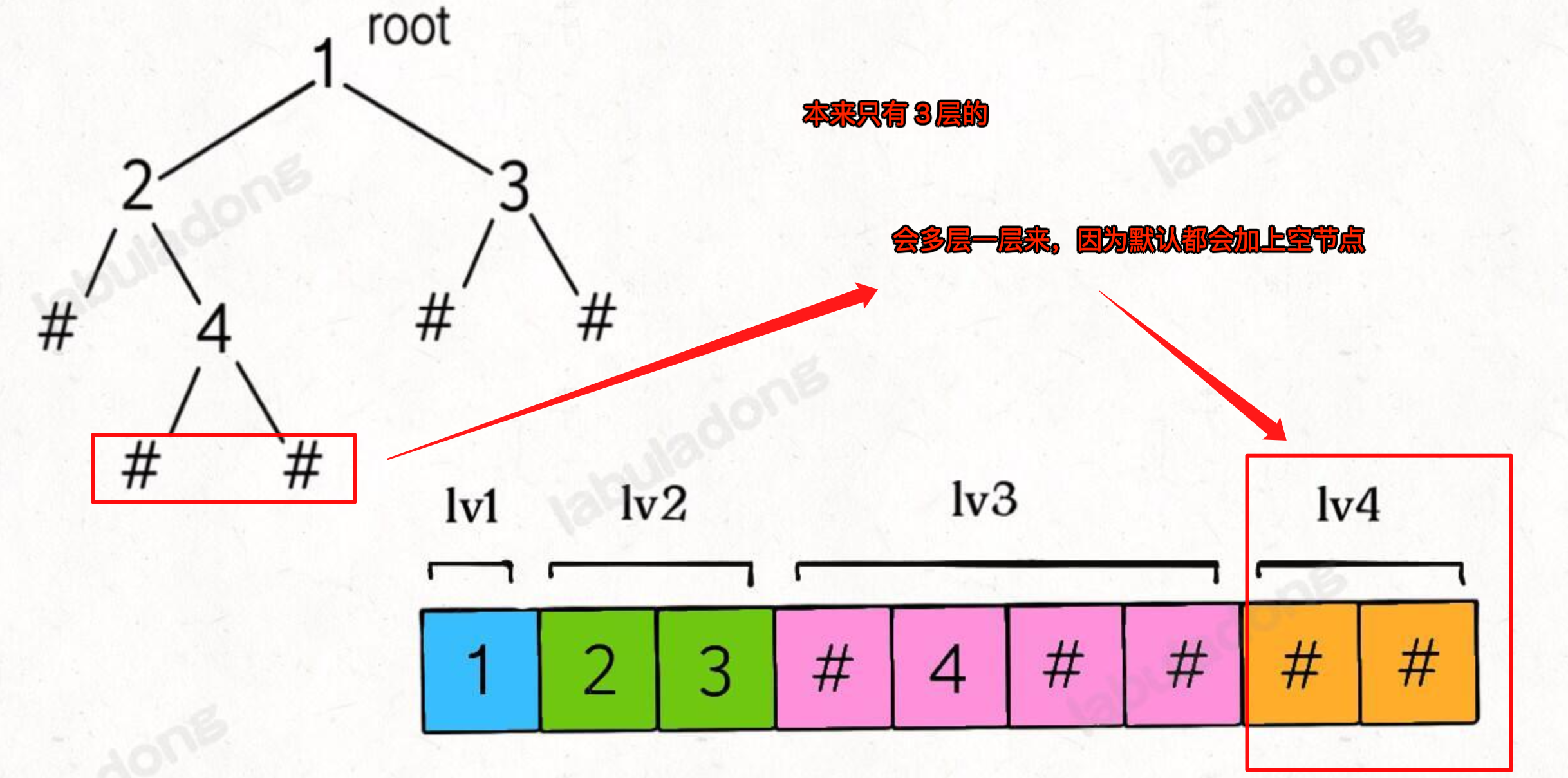
- 会多出一层来,别被下图无界了
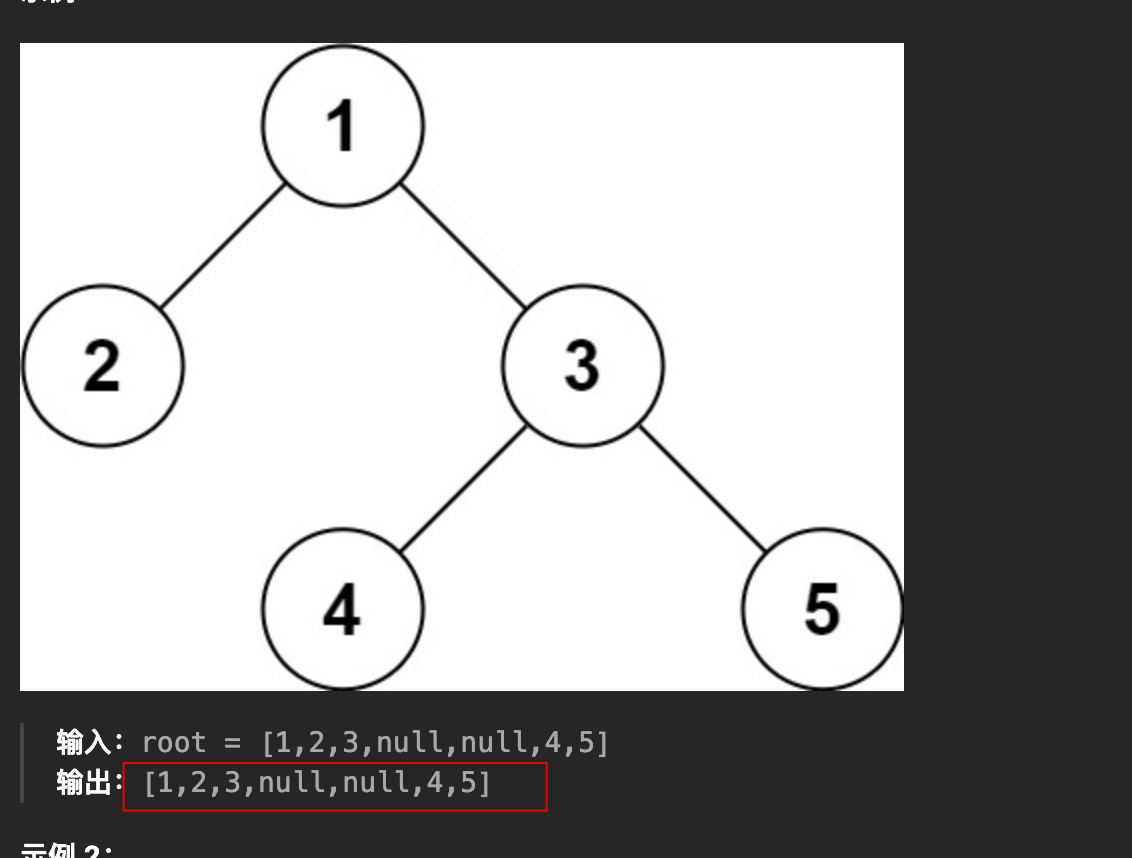
- 上图中,觉得序列化的结果应该是
1,2,3,#,#,5- 但其实是:
1,2,3,#,#,5,#,#,#,#- 多出一层,又比如下图
- 多出一层,又比如下图
- 但其实是:
- 上图中,觉得序列化的结果应该是
var serialize = function (root) {
let res = [];
let q = [root];
while (q.length) {
let size = q.length;
for (let i = 0; i < size; i++) {
let node = q.shift();
if (!node) {
res.push("#");
continue;
}
res.push(node.val);
q.push(node.left);
q.push(node.right);
}
}
return res.join(",");
};
反序列化
- 关键点:
if (data === "#") return null;- 搞了很久,因为 base case有问题
- 构造树一定包括
- 构造 root
- 构造 left
- 构造 right
- 因为这个层次遍历,没有递归遍历左右子树
var deserialize = function (data) {
console.log("data:", data);
// 1. 处理空树情况
if (data === "#") return null;
let arr = data.split(",");
let root = new TreeNode(parseInt(arr[0]));
let q = [root];
let index = 1;
while (q.length) {
let size = q.length;
for (let i = 0; i < size; i++) {
let node = q.shift();
// 构造左树
let left = arr[index++];
console.log("left***", left);
if (left !== "#") {
node.left = new TreeNode(parseInt(left));
q.push(node.left);
}
// 构造右树
let right = arr[index++];
if (right !== "#") {
node.right = new TreeNode(parseInt(right));
q.push(node.right);
}
}
}
return root;
};
5. 附:各种遍历是否能够确定二叉树
| 遍历组合 | 是否可以唯一确定树 |
|---|---|
| 仅前序 | 否 |
| 仅中序 | 否 |
| 仅后序 | 否 |
| 前序+中序 | 是 |
| 中序+后序 | 是 |
| 前序+后序 | 不一定(取决于树的结构) |
| 前序(包括空指针) | 是 |
| 后序(包括空指针) | 是 |
| 中序(包括空指针) | 否 |
6. 更多
- https://labuladong.online/algo/data-structure/serialize-and-deserialize-binary-tree/