省份数量

#leetcode #算法 #DFS #算法/图

1. 总结

var findCircleNum = function (isConnected) { // isConnected 是邻接矩阵
  let n = isConnected.length;
  let visited = new Array(n).fill(false);
  let res = 0;
  for (let i = 0; i < n; i++) {
    if (!visited[i]) {
      dfs(i);
      res++;
    }
  }
  function dfs(city) {
    visited[city] = true;
    for (let i = 0; i < n; i++) {
      if (isConnected[city][i] === 1 && !visited[i]) {
        dfs(i);
      }
    }
  }
  return res;
};

2. 题目及理解

547. 省份数量

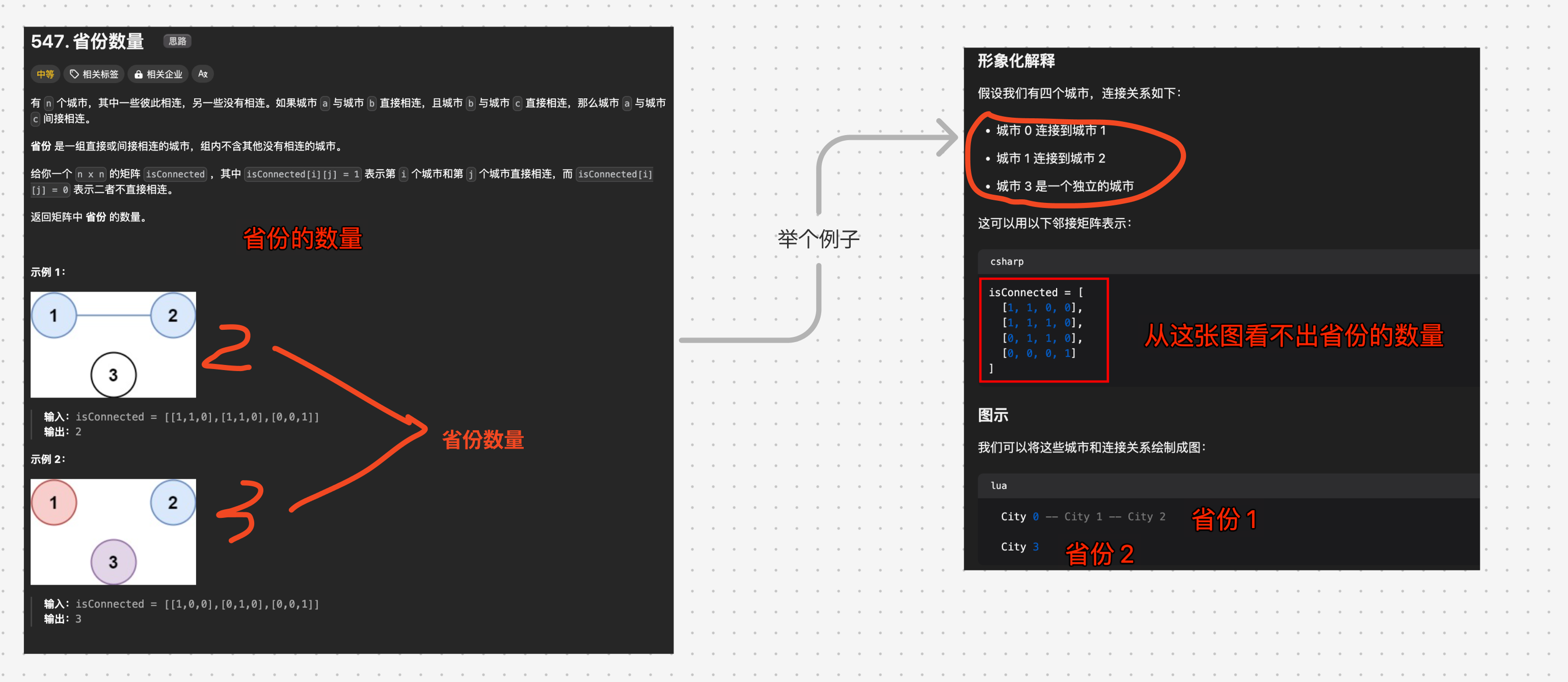
cos-blog-832-34-20241012|1128

省份是一组间接或直接连接的城市

3. 思路一：DFS

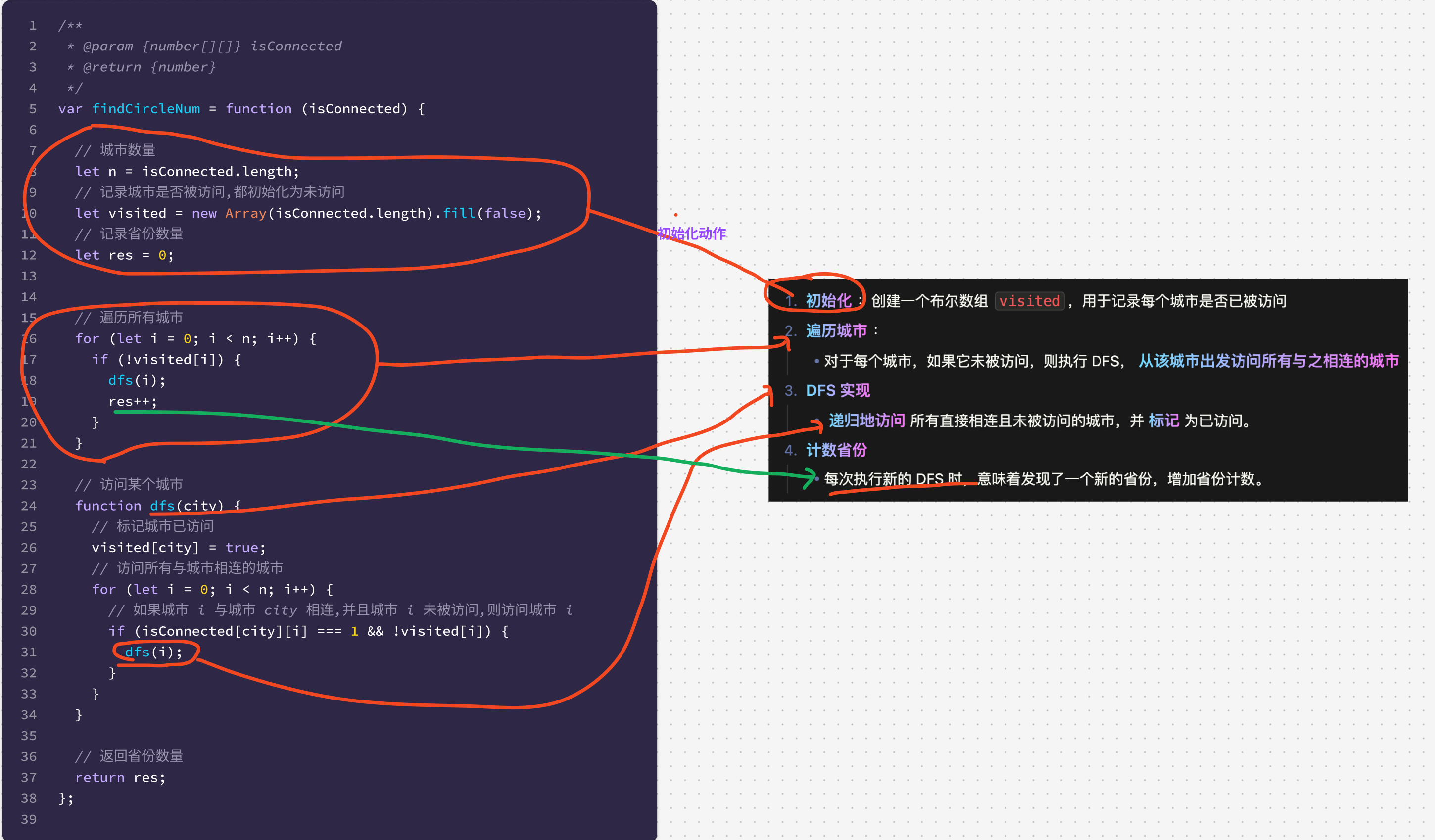
初始化：创建一个布尔数组 visited，用于记录每个城市是否已被访问
遍历城市：
- 对于每个城市，如果它未被访问，则执行 DFS，从该城市出发访问所有与之相连的城市
DFS 实现
- 递归地访问所有直接相连且未被访问的城市，并标记为已访问。
计数省份
- 每次执行新的 DFS 时，意味着发现了一个新的省份，增加省份计数。

3.1. 代码实现及分析

cos-blog-832-34-20241012

3.2. 源码

/**
 * @param {number[][]} isConnected
 * @return {number}
 */
var findCircleNum = function (isConnected) {
  // 城市数量
  let n = isConnected.length;
  // 记录城市是否被访问,都初始化为未访问
  let visited = new Array(isConnected.length).fill(false);
  // 记录省份数量
  let res = 0;

  // 访问某个城市
  function dfs(city) {
    // 标记城市已访问
    visited[city] = true;
    // 访问所有与城市相连的城市
    for (let i = 0; i < n; i++) {
      // 如果城市 i 与城市 city 相连,并且城市 i 未被访问,则访问城市 i
      if (isConnected[city][i] === 1 && !visited[i]) {
        dfs(i);
      }
    }
  }

  // 遍历所有城市
  for (let i = 0; i < n; i++) {
    if (!visited[i]) {
      dfs(i);
      res++;
    }
  }

  // 返回省份数量
  return res;
};