滑动谜题

773. 滑动谜题

1. 总结

关键点：

思路，看着这图就明白了
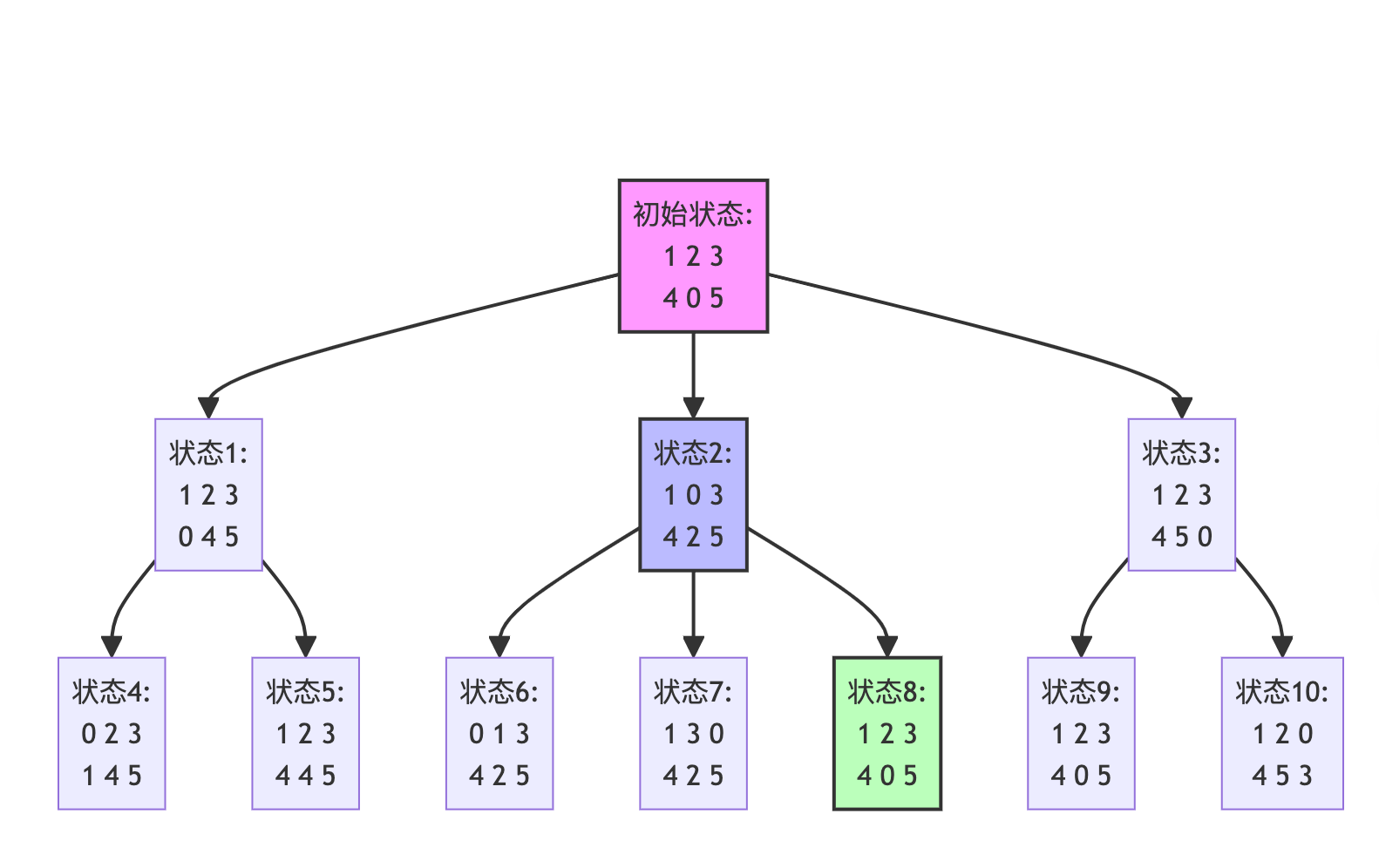
- 所以，关键点就是需要把二维数组转成一维数组，方便做 BFS
  - 并且需要构建一维数组的 maping 关系
需要添加 visited 检测
mapping 提前写好，规则见下面
- 如何使用 let index = str.indexOf("0");
  - 找到当前 0 的位置，然后更换位置
swap 函数
- 字符串是不可变的，需要转换成数组

/**
 * @param {number[][]} board
 * @return {number}
 */
var slidingPuzzle = function (board) {
    let target = "123450"
    let m = board.length;
    let n = board[0].length;
    let start = "";
    for (let item of board) {
        start += item.join("");
    }
    
    // 1. 添加 visited 集合来避免重复访问
    let visited = new Set();
    visited.add(start);
    
    let q = [start];
    let step = 0;
    
    // 2. 修改 BFS 实现，按层遍历
    while (q.length) {
        let size = q.length;
        // 遍历当前层的所有节点
        for (let i = 0; i < size; i++) {
            let cur = q.shift();
            if (cur === target) return step;
            let nodes = getNodes(cur);
            for (let node of nodes) {
                // 3. 添加访问检查
                if (!visited.has(node)) {
                    q.push(node);
                    visited.add(node);
                }
            }
        }
        step++;
    }

    return -1;

    function getNodes(str) {
        let index = str.indexOf("0");
        let res = [];
        let mapping = {
            0: [1, 3],
            1: [0, 2, 4],
            2: [1, 5],
            3: [0, 4],
            4: [1, 3, 5],
            5: [2, 4]
        };
        let arr = mapping[index];
        for(let item of arr){
            res.push(swap(str, index, item));
        }
        return res;
    }

    // 4. 修复 swap 函数
    function swap(str, i, j) {
        // 字符串是不可变的，需要转换成数组
        let arr = str.split('');
        // 交换位置
        [arr[i], arr[j]] = [arr[j], arr[i]];
        // 转回字符串
        return arr.join('');
    }
};

2. 题目

图片&文件

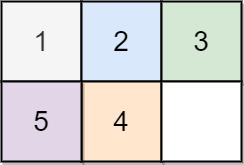
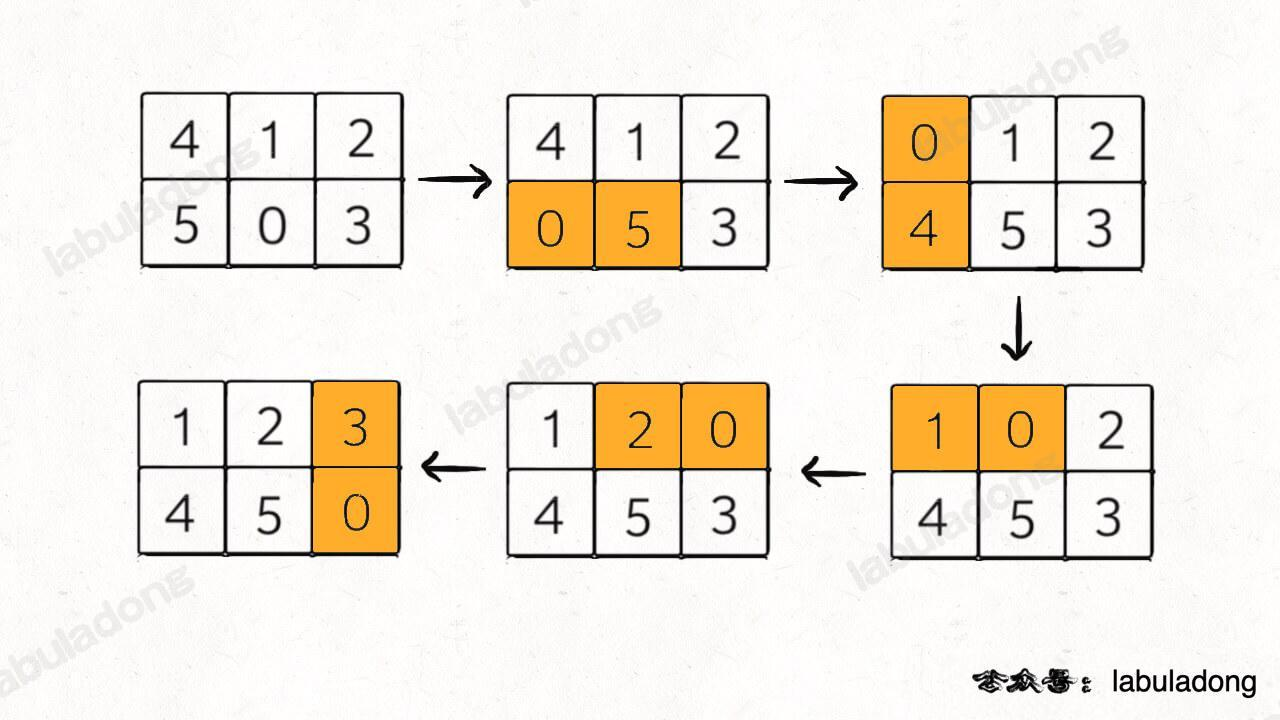
类似的拼图游戏

图片&文件

3. 思路

如何穷举出 board 当前局面下可能==衍生出的所有局面==
- 看数字 0 的位置呗，和上下左右的数字进行交换就行了，如下图：

图片&文件

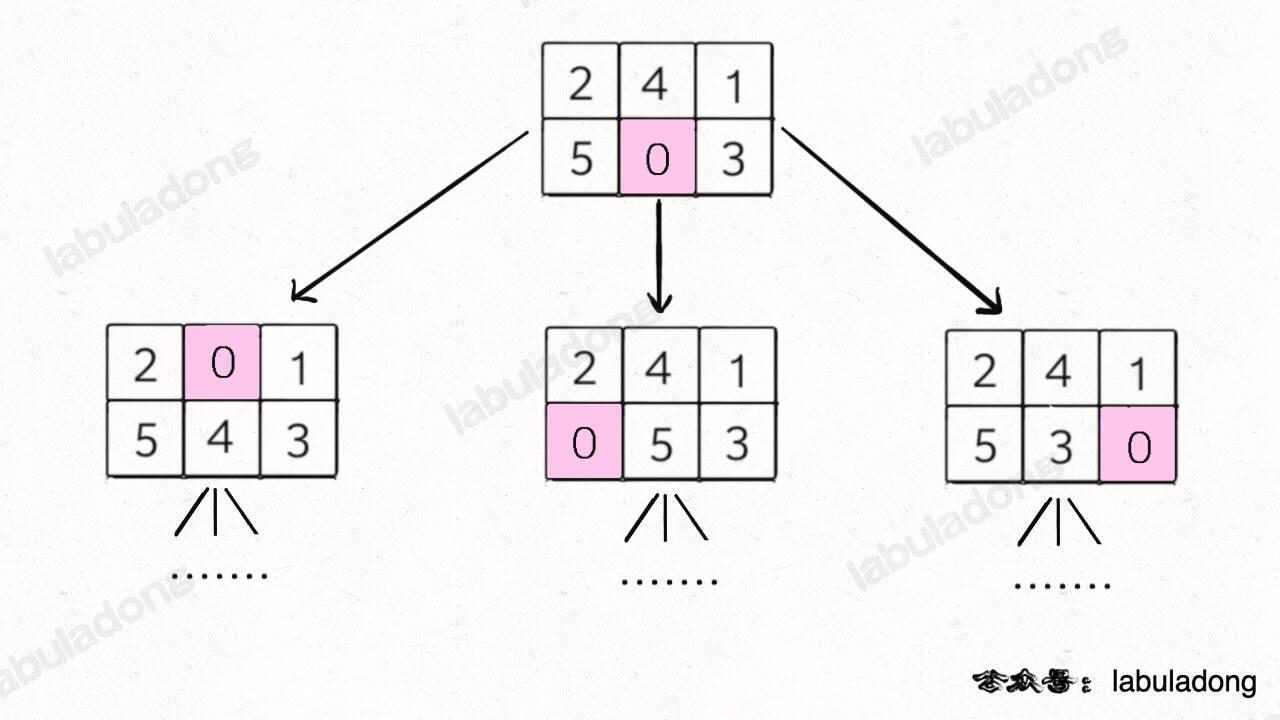
这样就是一个 BFS 问题
- 每次先找到数字 0，然后和周围的数字进行交换，形成新的局面加入队列……
- 当第一次到达 target 时，就得到了赢得游戏的==最少步数==

4. mapping 的分析过程

4.1. 棋盘结构

首先我们看 2×3 的棋盘结构，把每个位置标上序号：

0 1 2
3 4 5

4.2. 移动规则

在滑动谜题中，每个位置只能和相邻的位置交换（上下左右）
相邻 = 在同一行或同一列，且紧挨着

4.3. 分析每个位置

让我们逐个分析每个位置可以移动到哪些位置：

4.3.1. 位置 0：

[0] 1  2
 3  4  5

右边是位置 1
下边是位置 3
所以位置 0 可以移动到：[1, 3]

4.3.2. 位置 1：

 0 [1] 2
 3  4  5

左边是位置 0
右边是位置 2
下边是位置 4
所以位置 1 可以移动到：[0, 2, 4]

4.3.3. 位置 2：

 0  1 [2]
 3  4  5

左边是位置 1
下边是位置 5
所以位置 2 可以移动到：[1, 5]

4.3.4. 位置 3：

 0  1  2
[3] 4  5

上边是位置 0
右边是位置 4
所以位置 3 可以移动到：[0, 4]

4.3.5. 位置 4：

 0  1  2
 3 [4] 5

上边是位置 1
左边是位置 3
右边是位置 5
所以位置 4 可以移动到：[1, 3, 5]

4.3.6. 位置 5：

 0  1  2
 3  4 [5]

上边是位置 2
左边是位置 4
所以位置 5 可以移动到：[2, 4]

4.4. 总结

所以最终得到的移动映射关系是：

const neighbors = {
    0: [1, 3],
    1: [0, 2, 4],
    2: [1, 5],
    3: [0, 4],
    4: [1, 3, 5],
    5: [2, 4]
};

4.5. 理解要点

这个映射关系是固定的，因为：
- 棋盘大小是固定的（2×3）
- 每个位置的相邻关系是固定的
在实际解题时：
- 这个映射表只需要创建一次
- 可以作为常量使用
- 用来确定空格（0）可以和哪些位置交换
使用场景：

// 假设当前状态中 0 在位置 1
// 我们可以通过 neighbors[1] 得知
// 0 可以移动到位置 0、2、4
// 也就是说可以和这些位置的数字进行交换

这样设计的好处是：

避免每次都要计算可移动的位置
提高代码的可读性和维护性
减少出错的可能性

liguwe's site

滑动谜题

目录

1. 总结

2. 题目

3. 思路

4. mapping 的分析过程

4.1. 棋盘结构

4.2. 移动规则

4.3. 分析每个位置

4.3.1. 位置 0：

4.3.2. 位置 1：

4.3.3. 位置 2：

4.3.4. 位置 3：

4.3.5. 位置 4：

4.3.6. 位置 5：

4.4. 总结

4.5. 理解要点