找链表中第一个入环节点

142. 环形链表 II

目录

• 总结
• 代码
• 题意
• 思路
• 推导过程
• 最终代码

总结

• 快慢指针
• ==相遇时==，做三件事情
  • ① 改成同速前进
  • ② 记录：slow ==重新指向==头节点
    • slow = head;
  • ③ 第一次相遇时 ==break==
  • 当然：如果没有环，提前返回
• ==再次相遇==的节点位置就是 环开始的位置
  • while (slow !== fast) {

代码

var detectCycle = function (head) {
  let fast = head;
  let slow = head;

  // 第一次相遇时 break
  while (fast && fast.next) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow === fast) {
      break;
    }
  }

  // 没有环，提前返回
  if (fast === null || fast.next === null) {
    return null;
  }

  // 同速前进
  slow = head;
  while (slow !== fast) {
    slow = slow.next;
    fast = fast.next;
  }

  return slow;
};

题意

如果已经已知链表中含有环，如何计算这个环的起点？

如果不包含环，返回 null

思路

• 当快慢指针相遇时，让其中任一个指针指向头节点
• 然后让它俩以相同速度前进，再次相遇时所在的节点位置就是==环开始的位置==

推导过程

假设快慢指针相遇时，慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步，且 ==K 一定是环长度的整数倍==，如下图：

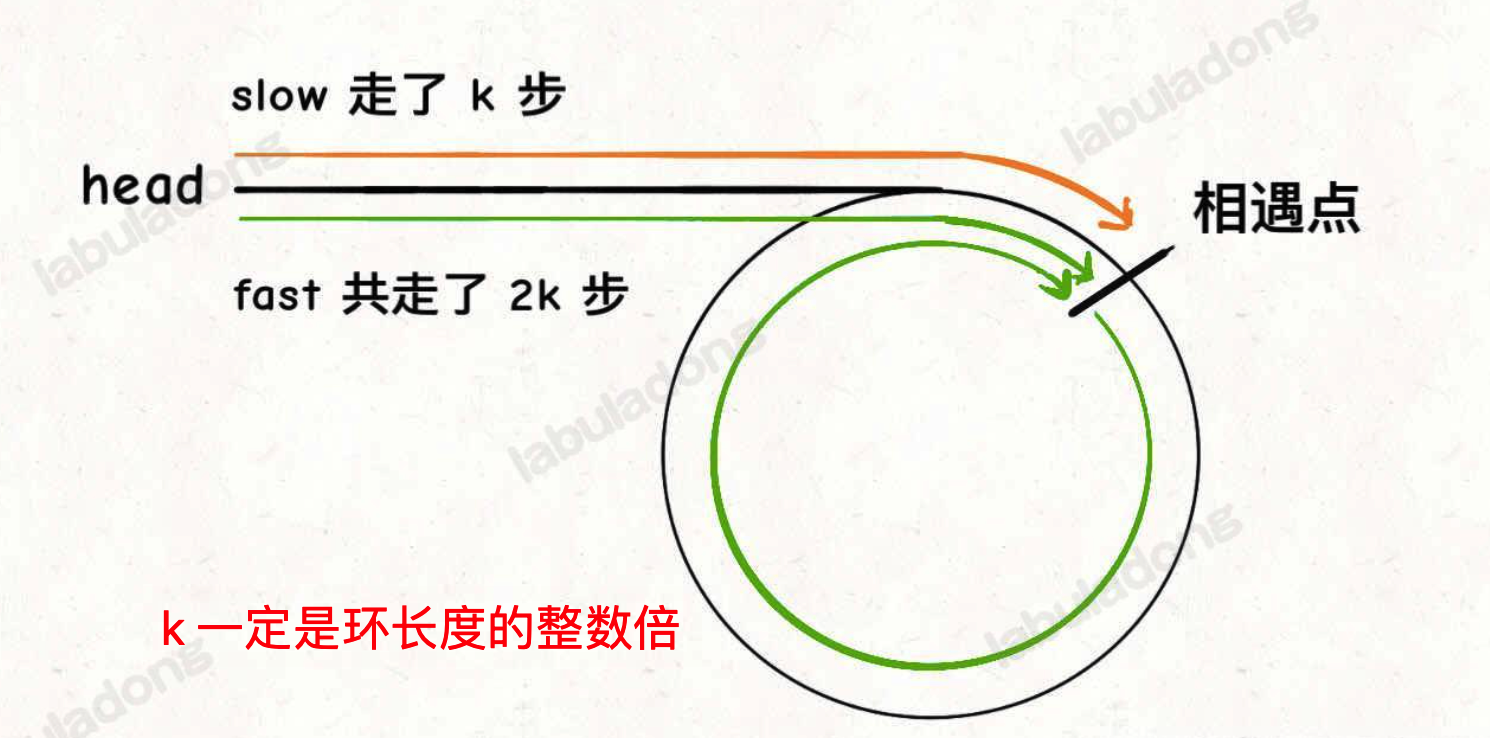
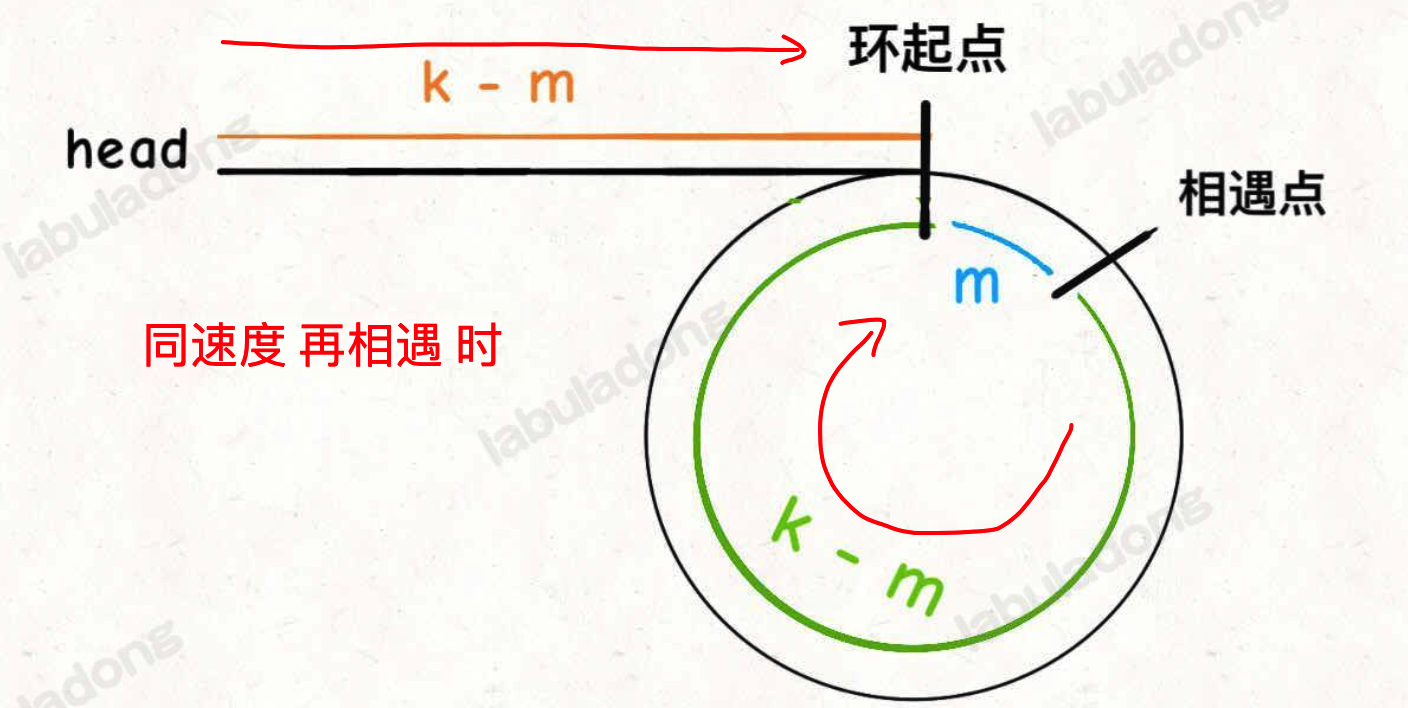
再假设相遇点距环的起点的距离为 m ， 那么结合上图的 slow 指针，环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到 达环起点。 巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。因为结合上图的 fast 指针，从相遇点开始走k步可以转回到相遇点，那走 k - m 步肯定就走到环起点了 所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后一定会相遇，相遇之处就是环的起点了。

最终代码

var detectCycle = function (head) {
    var fast, slow;
    fast = slow = head;
    //// ::::第一步： 相遇时，即相遇点，
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast === slow) break;
    }
    // 上面的代码类似 hasCycle 函数
    if (fast == null || fast.next == null) {
        // fast 遇到空指针说明没有环
        return null;
    }
    // ::::第二步：在相遇点，重新同速度前进
    
    // 重新指向头结点
    slow = head;
    // 快慢指针同步前进，相交点就是环起点
    while (slow !== fast) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
};