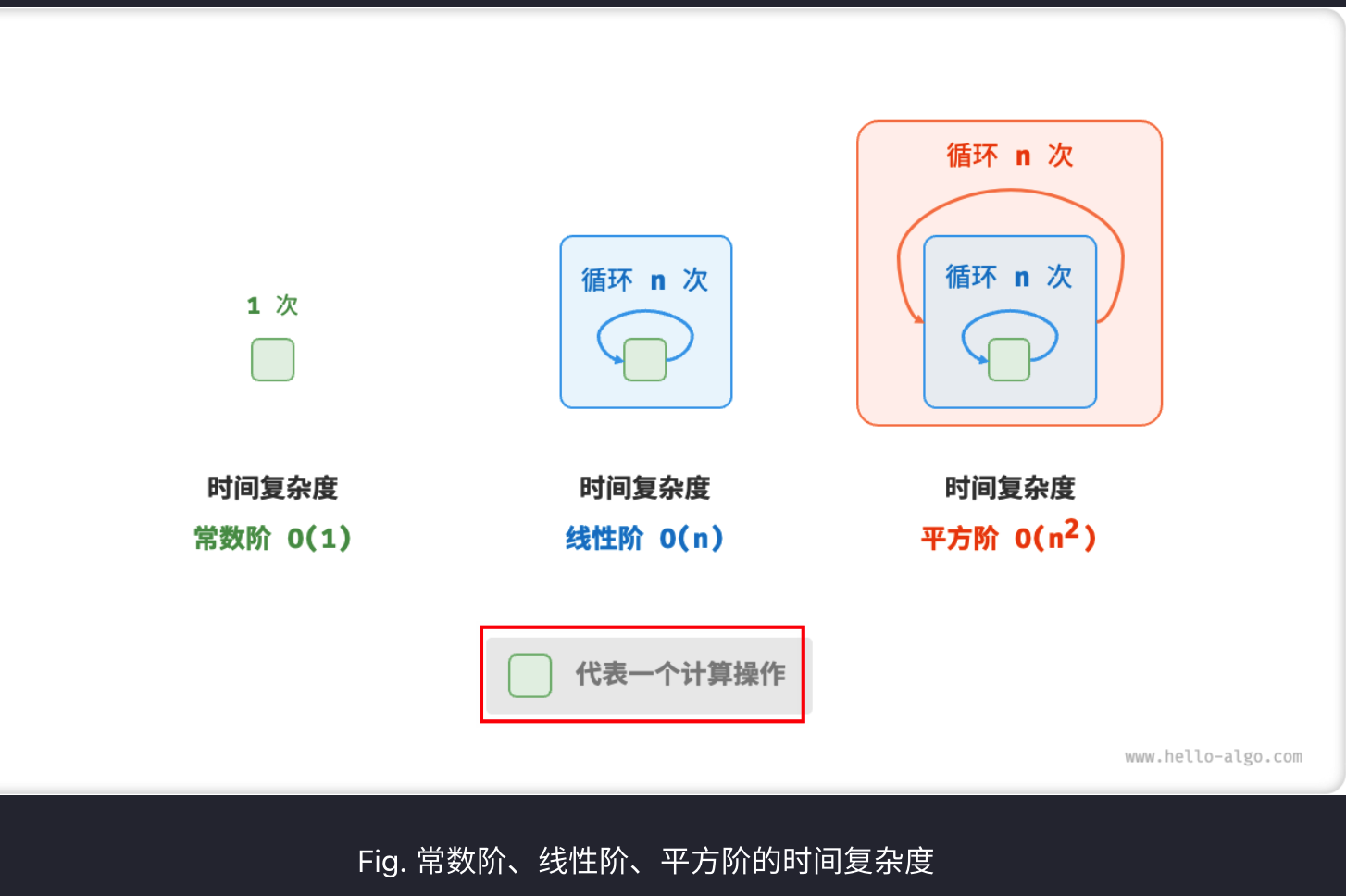
算法复杂度
#算法/基础
[!info]
- 空间复杂度的计算的方式可以再读读,挺有意思
目录
一、综述
- 数据结构和算法解决是 “如何让计算机更快时间、更省空间的解决问题”。
- 因此需从
执行时间和占用空间两个维度来评估数据结构和算法的性能。 - 分别用
时间复杂度和空间复杂度两个概念来描述性能问题,二者统称为复杂度。 - 复杂度描述的是算法
执行时间(或占用空间)与数据规模的增长趋势关系。
二、时间复杂度
(一)什么是时间复杂度
统计的是 算法运行时间随着数据量变大时的 增长趋势 ,而不是 具体运行时间
下面函数展示了随着 n 的增加,算法的 时间的复杂度
// 算法 A 时间复杂度:常数阶
function algorithm_A(n) {
console.log(0);
}
// 算法 B 时间复杂度:线性阶
function algorithm_B(n) {
for (let i = 0; i < n; i++) {
console.log(0);
}
}
// 算法 C 时间复杂度:常数阶
function algorithm_C(n) {
for (let i = 0; i < 1000000; i++) {
console.log(0);
}
}
上面代码的的增长趋势如下图:
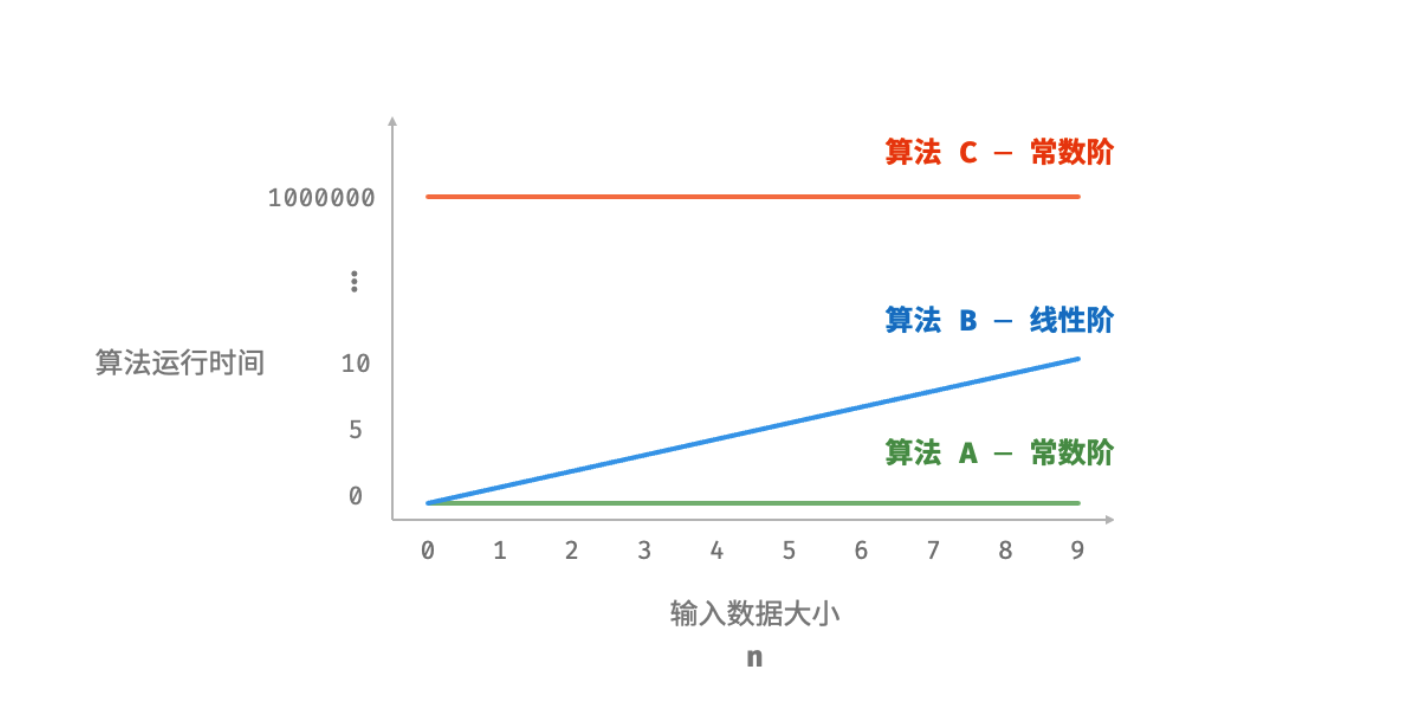 时间复杂度由多项式
时间复杂度由多项式 T(n) 中最高阶的项来决定。这是因为在趋于无穷大时,最高阶的项将发挥主导作用,其他项的影响都可以被忽略。即 “系数无法撼动阶数” , 当趋于无穷大时,这些常数变得无足轻重,如下图:

(二)如何计算时间复杂度
function aFun() {
console.log("Hello, World!"); // 需要执行 1 次
return 0; // 需要执行 1 次
}
// 需要执行 2 次运算
function bFun(n) {
for(let i = 0; i < n; i++) { // 需要执行 (n + 1) 次
console.log("Hello, World!"); // 需要执行 n 次
}
return 0; // 需要执行 1 次
}
// 需要执行 ( n + 1 + n + 1 ) = 2n +2 次运算
function cal(n) {
let sum = 0; // 1 次
let i = 1; // 1 次
let j = 1; // 1 次
for (; i <= n; ++i) { // n 次
j = 1; // n 次
for (; j <= n; ++j) { // n * n ,也即是 n平方次
sum = sum + i * j; // n * n ,也即是 n平方次
}
}
}
// 那么这个方法需要执行 ( n^2 + n^2 + n + n + 1 + 1 +1 ) = 2n^2 +2n + 3
如下图:
(三)几个时间复杂度的分析原则
- 只关注
循环执行次数最多的一段代码,即 “系数无法撼动阶数” - 加法法则:总复杂度 等于 量级最大 的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于 嵌套内外代码复杂度的乘积
- 多个规模求加法:
O(m+n) - 多个规模求乘法:
O(m*n)
(四)常见的算法时间复杂度
1、常数阶:O(1)
/* 常数阶 */
function constant(n) {
let count = 0;
const size = 100000; // size 是固定的
for (let i = 0; i < size; i++) count++;
return count;
}
2、线性阶:O(n)
通常出现在单层循环中,遍历数组和遍历链表等操作的时间复杂度均为 O(n)
3、平方阶:O(n^2)
通常出现在 嵌套循环 中,如冒泡排序。
[!info]
4、指数阶:O(2^n)
- 实际场景,细胞分裂:初始状态为
1个细胞,分裂一轮后变为2个,分裂两轮后变个4细胞 …

指数阶常出现于递归函数中,如下代码:
/* 指数阶(递归实现) */
function expRecur(n) {
if (n == 1) return 1;
return expRecur(n - 1) + expRecur(n - 1) + 1;
}
5、对数阶:O(log n)
- 与
指数阶相反,对数阶反映了 “每轮缩减到一半的情况” - 常出于「二分查找」和「分治算法」中
每轮缩减到一半的代码示例及图例如下:
/* 对数阶(循环实现) */
function logarithmic(n) {
let count = 0;
while (n > 1) {
n = n / 2;
count++;
}
return count;
}

- 与
指数阶一样,对数阶也常出于递归函数中,如下代码
/* 对数阶(递归实现) */
function logRecur(n) {
if (n <= 1) return 0;
return logRecur(n / 2) + 1;
}
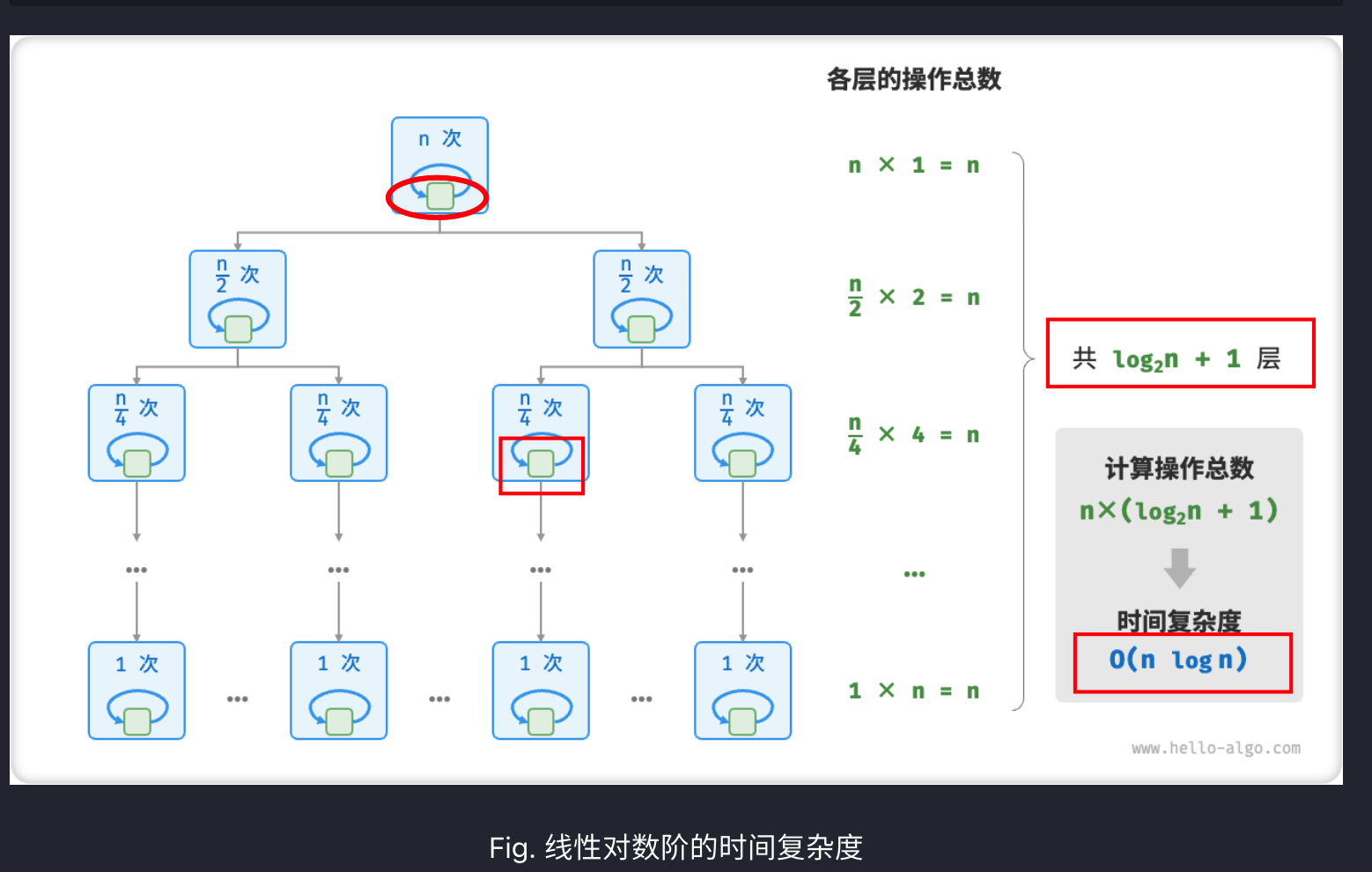
6、线性对数阶:O(n*log n)
如主流排序算法 快速排序、归并排序、堆排序等
7、阶乘阶:O(n!)
即 「全排列」 问题
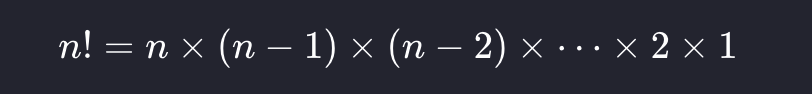
[!question] 画出一张
阶乘阶的 分裂图?
(五)最差、最佳、平均时间复杂度
「最差时间复杂度」更为实用,因为它给出了一个 “效率安全值”- 至于其他,如
平均情况时间复杂度等忽略吧
三、空间复杂度
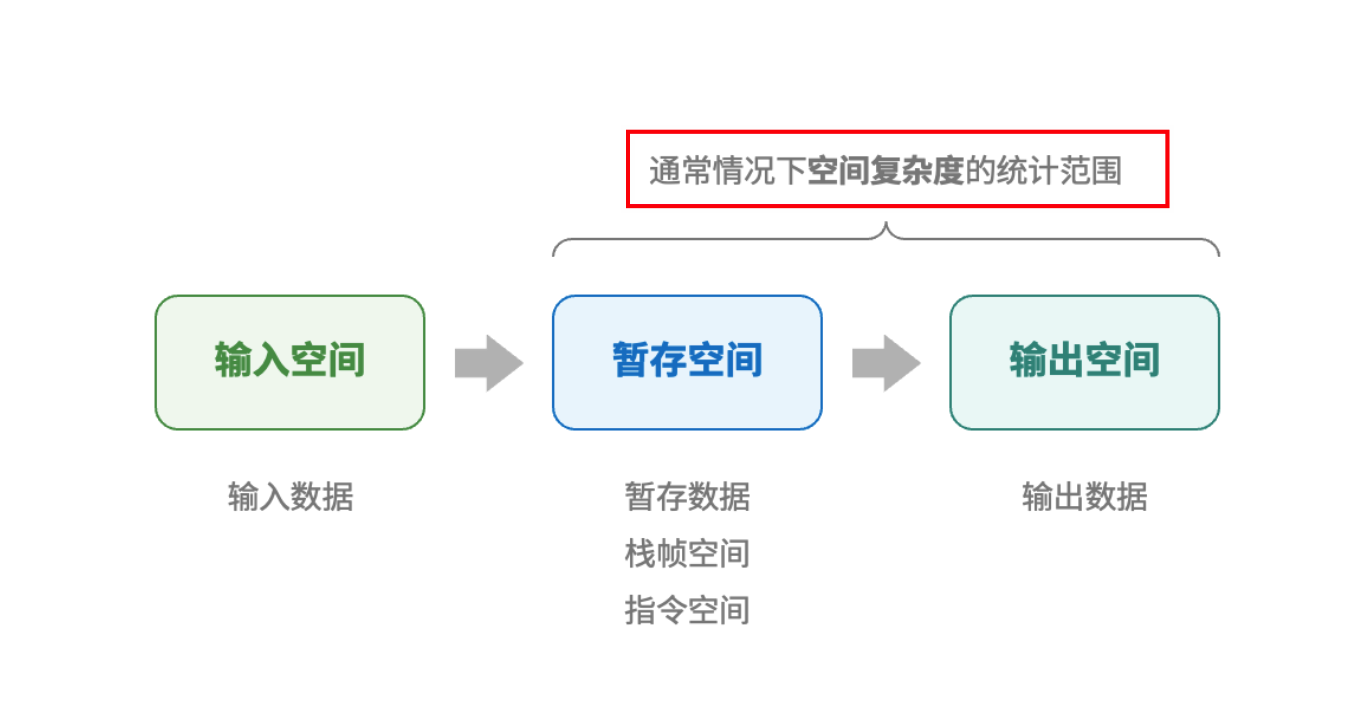
「空间复杂度 Space Complexity」用于衡量算法使用内存空间随着数据量变大时的增长趋势
(一)算法相关 空间
- 「输入空间」 用于存储算法的输入数据。
- 「暂存空间」 用于存储算法运行过程中的变量、对象、函数上下文等数据。
- 「暂存数据」用于保存算法运行过程中的各种常量、变量、对象等。
- 「栈帧空间」用于保存调用函数的上下文数据。
- 系统在每次调用函数时都会在栈顶部
创建一个栈帧, - 函数返回后,栈帧空间会被
释放。
- 系统在每次调用函数时都会在栈顶部
- 「指令空间」用于保存编译后的程序指令,在实际统计中
通常忽略不计。
- 「输出空间」 用于存储算法的输出数据。
/* 类 */
class Node {
val;
next;
constructor(val) {
this.val = val === undefined ? 0 : val; // 节点值
this.next = null; // 指向下一节点的引用
}
}
/* 函数 */
function constFunc() {
// do something
return 0;
}
function algorithm(n) { // 输入数据: 输入空间,即函数
const a = 0; // 暂存数据(常量)
let b = 0; // 暂存数据(变量)
const node = new Node(0); // 暂存数据(对象)
const c = constFunc(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据:返回数据,即 return
}
(二)如何推算空间复杂度
通常只关注 最差空间复杂度 , 看下面代码就懂了,因为我们必须要有 足够的内存空间预留,所以:
- 以
最差输入数据为准 - 以算法运行过程中的
峰值内存为准
function algorithm(n) {
const a = 0; // O(1)
const b = new Array(10000); // O(1)
if (n > 10) {
const nums = new Array(n); // O(n)
}
}
以下代码的空间复杂度分析:
function constFunc() {
// do something
return 0;
}
/* 循环 O(1) */
// 因为每轮循环后,调用的函数都会 释放了栈帧空间,所以空间复杂度为 O(1)
function loop(n) {
for (let i = 0; i < n; i++) {
constFunc();
}
}
/* 递归 O(n) */
// 递归函数 recur() 在运行过程中会同时存在 个未返回的 recur()
// 所以,会有 O(n) 的栈帧空间
function recur(n) {
if (n === 1) return;
return recur(n - 1);
}
(三)常见的空间复杂度类型
1、常数阶:O(1)
常数阶常见于 数量与输入数据大小 n 无关的常量、变量、对象
/* 常数阶 */
function constant(n) {
// 常量、变量、对象占用 O(1) 空间
const a = 0;
const b = 0;
const nums = new Array(10000);
const node = new ListNode(0);
// 循环中的变量占用 O(1) 空间
for (let i = 0; i < n; i++) {
const c = 0;
}
// 循环中的函数占用 O(1) 空间
for (let i = 0; i < n; i++) {
constFunc();
}
}
[!tip] 需要注意的是,在循环中初始化变量或调用函数而占用的内存,在进入下一循环后就会被释放,即不会累积占用空间,空间复杂度仍为
O(1)
2、线性阶:O(n)
线性阶常见于 元素数量与 输入数据大小 n 成正比的数组、链表、栈、队列等。
/* 线性阶 */
function linear(n) {
// 长度为 n 的数组占用 O(n) 空间
const nums = new Array(n);
// 长度为 n 的列表占用 O(n) 空间
const nodes = [];
for (let i = 0; i < n; i++) {
nodes.push(new ListNode(i));
}
// 长度为 n 的哈希表占用 O(n) 空间
const map = new Map();
for (let i = 0; i < n; i++) {
map.set(i, i.toString());
}
}
以下递归函数会同时存在 n 个未返回的 algorithm() 函数, 会占用 O(n)大小的栈帧空间:
/* 线性阶(递归实现) */
function linearRecur(n) {
console.log(`递归 n = ${n}`);
if (n === 1) return;
linearRecur(n - 1);
}
如下图:

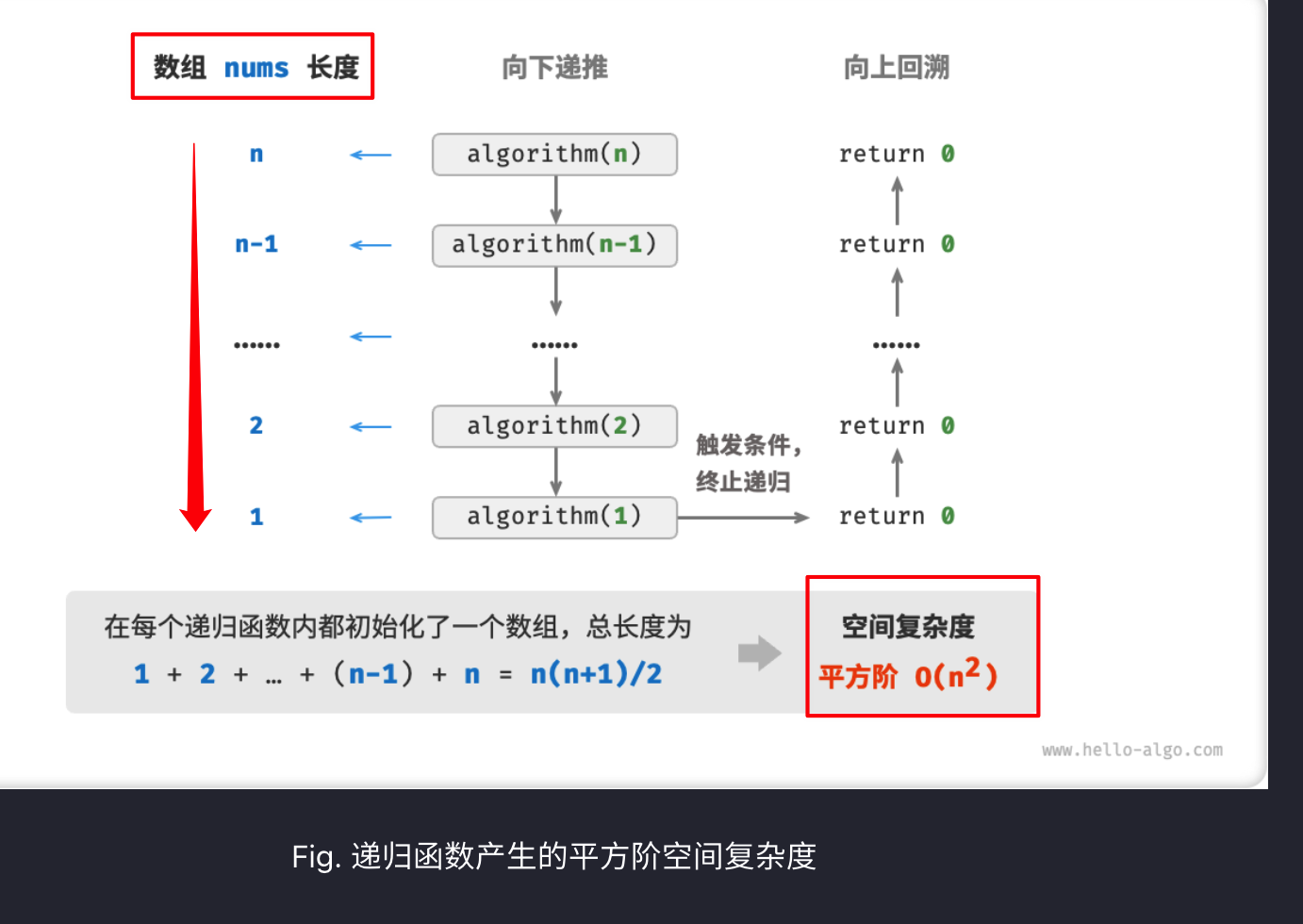
3、平方阶:O(n^2)
平方阶常见于矩阵 和 图 ,如下代码:
/* 平方阶 */
function quadratic(n) {
// 矩阵占用 O(n^2) 空间
const numMatrix = Array(n)
.fill(null)
.map(() => Array(n).fill(null));
// 二维列表占用 O(n^2) 空间
const numList = [];
for (let i = 0; i < n; i++) {
const tmp = [];
for (let j = 0; j < n; j++) {
tmp.push(0);
}
numList.push(tmp);
}
}
看看递归的场景:注意,需要关注 nums 的长度。
/* 平方阶(递归实现) */
function quadraticRecur(n) {
if (n <= 0) return 0;
const nums = new Array(n);
console.log(`递归 n = ${n} 中的 nums 长度 = ${nums.length}`);
return quadraticRecur(n - 1);
}
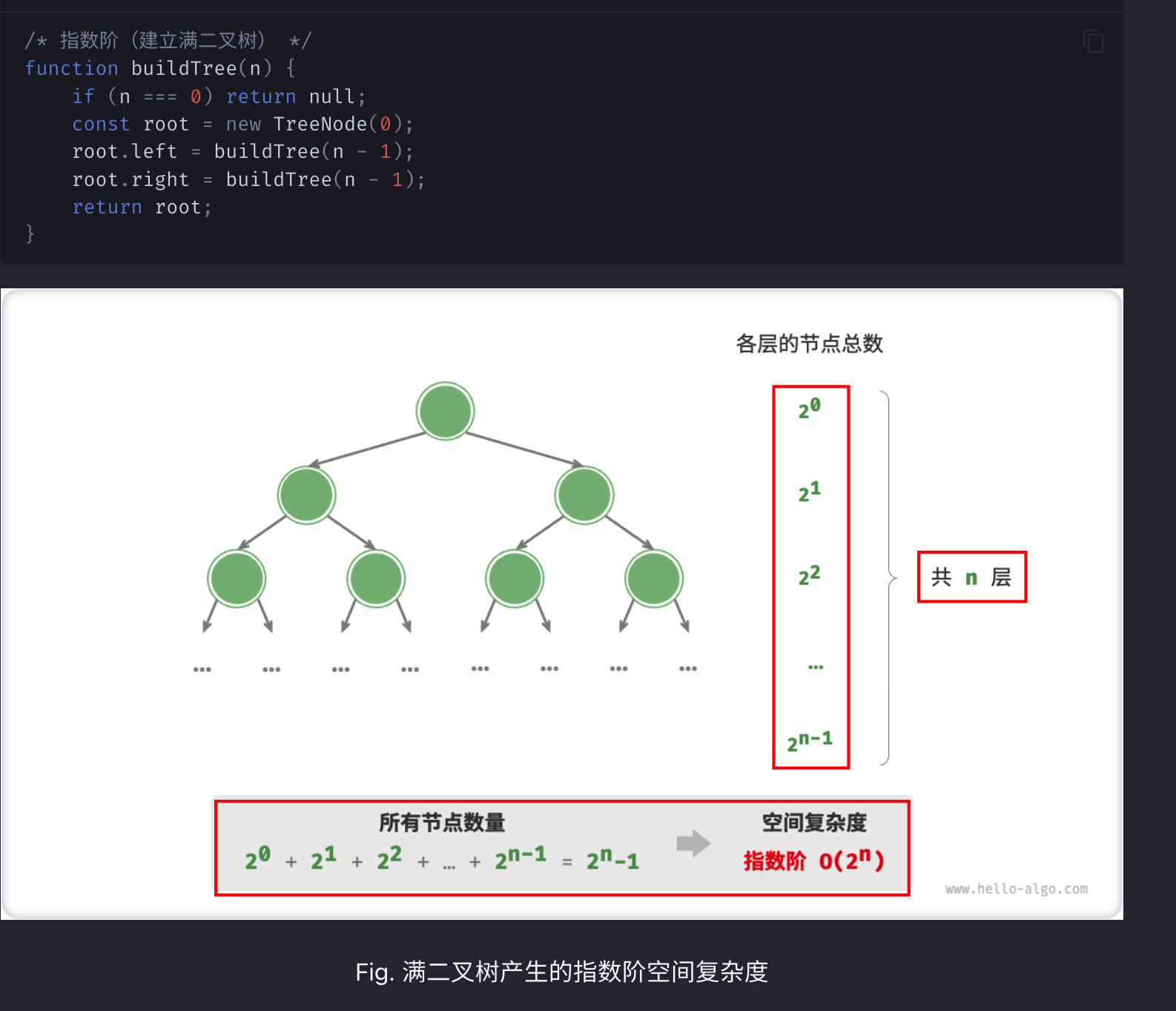
4、指数阶:O(2^n)
常见与构造二叉树,且关注最终的 节点个数,即占用的空间。

5、对数阶:O(log n)

[!question] 最后,数字转成字符串的表述,其实没太理解。
四、其他
- 理论上,尾递归函数的空间复杂度可以被优化为
O(1),但跟编程语言有关系 - 当前的计算机系统,以空间换时间场景较多
参考
https://www.hello-algo.com/chapter_computational_complexity/time_complexity/#222