二叉堆

#数据结构/二叉堆 #堆 #二叉堆

1. 堆、大顶堆、小顶堆的定义

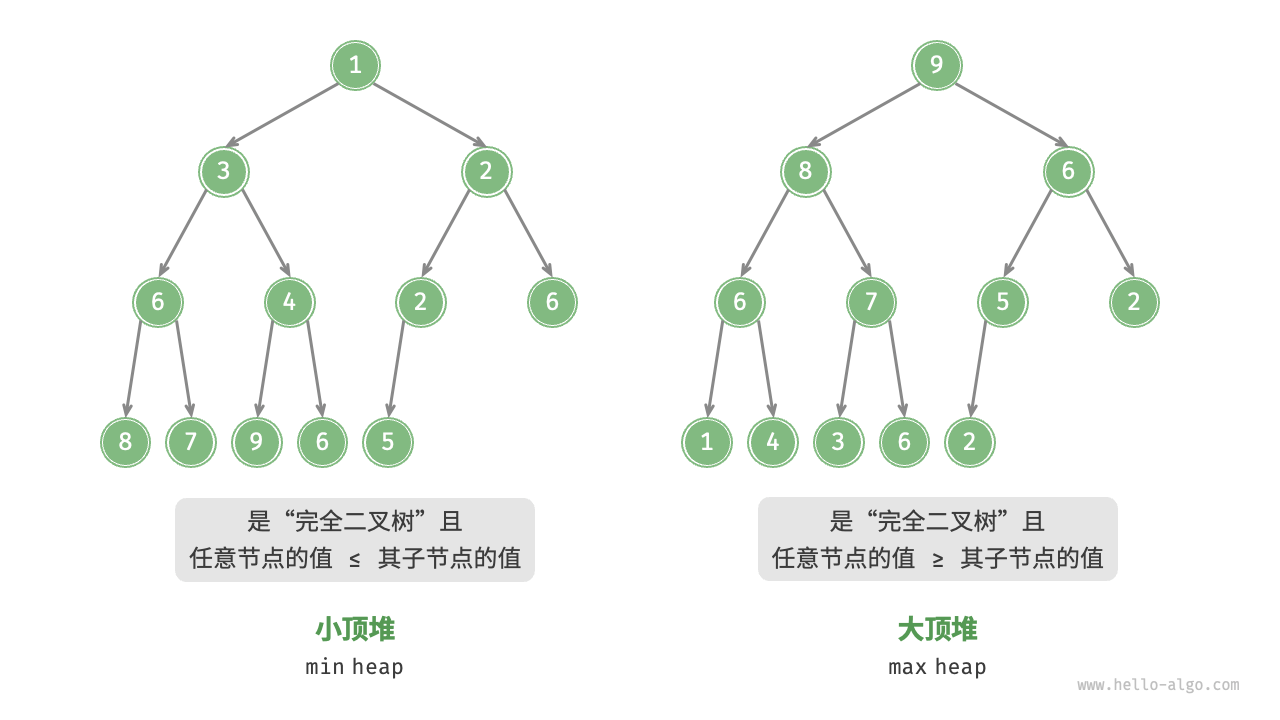
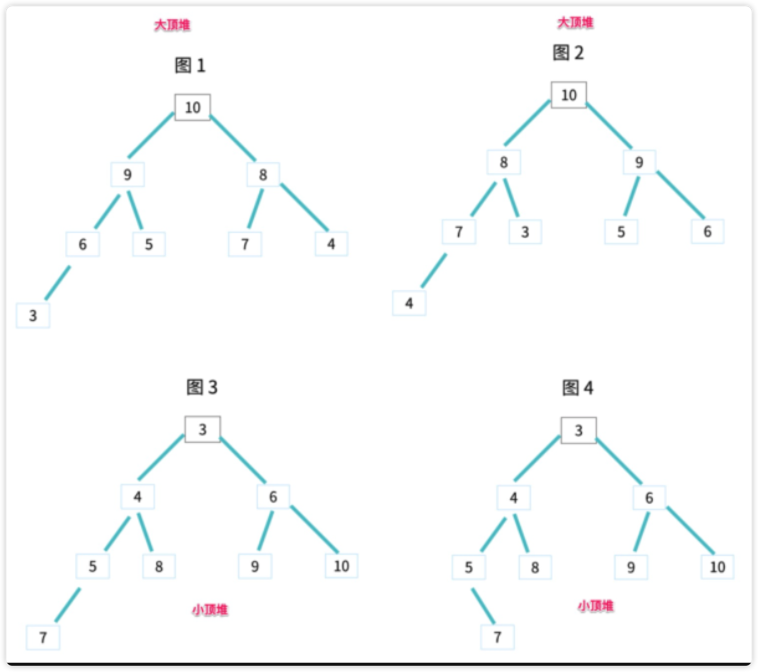
堆是一个完全二叉树，是一种能够动态排序的数据结构

堆中 每个节点的值都 大于等于（或者小于等于）其左右子节点的值
- 大的再上面，大顶堆，所以堆顶肯定是最大值
- 小的再上面，小顶堆，所以堆顶肯定是最小值

|528

2. 堆的存储结构表示

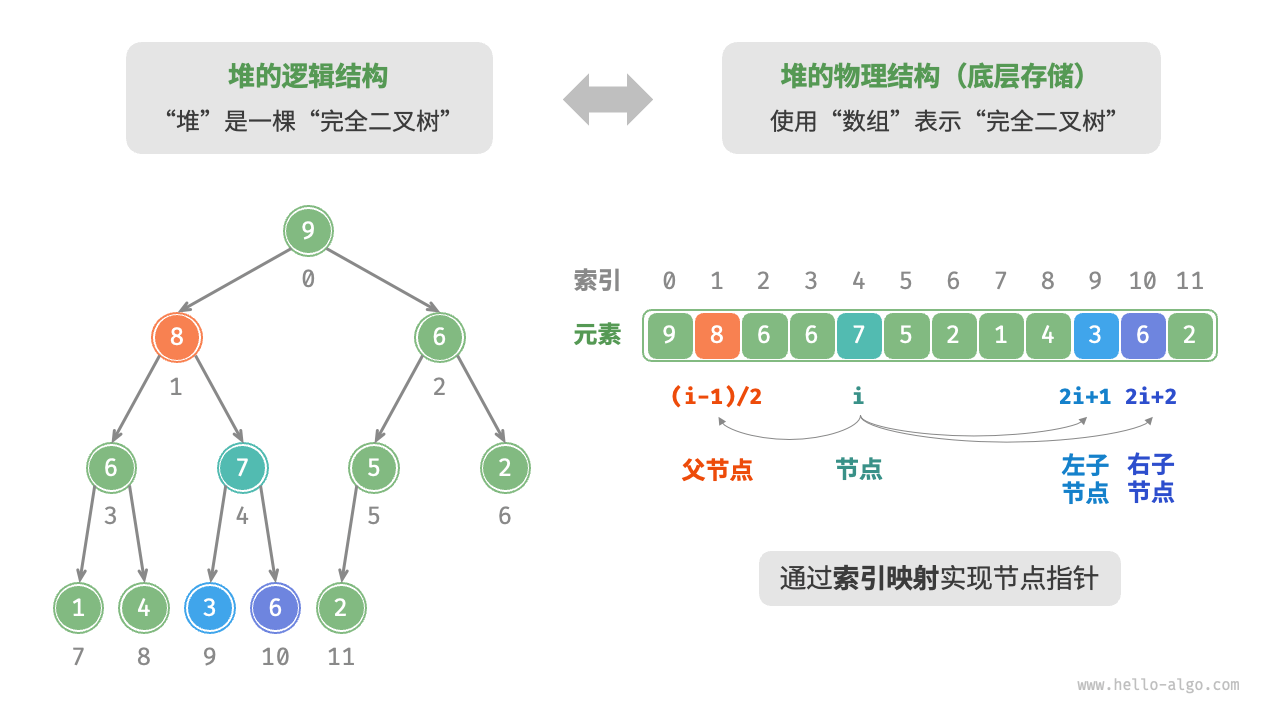
3. 堆的各个操作的复杂度

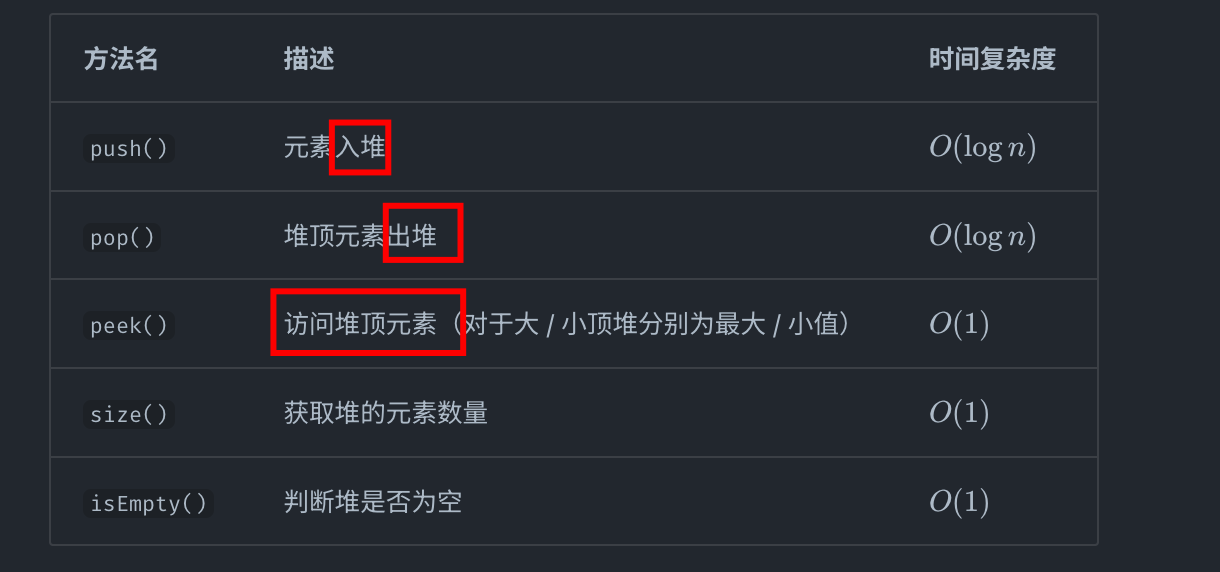
4. 堆的应用场景（或价值）

堆排序
大顶堆的价值
- 优先队列
- 高效排序
- 高效的动态中位数
小顶堆的价值
- 优先队列：小顶堆也常用于实现优先队列，支持快速获取和删除最小元素。
- 图算法：在图算法中，小顶堆用于实现 Dijkstra 最短路径算法和 Prim 最小生成树算法，以快速找到权重最小的边或路径。
- 合并有序列表：小顶堆可以高效地合并多个有序列表，例如用于外部排序或归并排序
堆的总体价值
- 高效的插入和删除操作：堆支持 O(log n) 的插入和删除操作，使其在需要频繁调整元素顺序的场景中非常高效。
- 内存利用率高：堆是一种基于数组实现的数据结构，内存利用率高，不需要额外的指针或链接。
- 广泛应用：堆在各种算法和系统中有广泛应用，包括调度系统、内存管理、图算法、实时数据处理等。

总之，堆结构因其高效的插入、删除和查找操作，在许多需要维护动态有序集合的场景中具有重要价值。

5. 代价

自动排序是有代价的，注意优先级队列 API 的时间复杂度，增删元素的复杂度是 O(logN)，其中 N 是当前二叉堆中的元素个数

6. Python 中的标准库 heapq

heapq 模块中提供。heapq 模块实现了最小堆（min heap）算法，但通过一些技巧也可以用来实现最大堆（max heap）。

以下是关于 Python 的 heapq 模块的一些关键信息：

6.1. 导入方式

import heapq

6.2. 主要函数

heapq.heapify(list): 将列表转换为堆
heapq.heappush(heap, item): 将元素添加到堆中
heapq.heappop(heap): 弹出并返回堆中最小的元素
heapq.heappushpop(heap, item): 将 item 放入堆中，然后弹出并返回堆中最小的元素
heapq.heapreplace(heap, item): 弹出并返回堆中最小的元素，然后将 item 放入堆中
heapq.nlargest(n, iterable, key=None): 返回 iterable 中 n 个最大的元素
heapq.nsmallest(n, iterable, key=None): 返回 iterable 中 n 个最小的元素

6.3. 使用示例

import heapq

# 创建一个堆
heap = []
heapq.heappush(heap, 4)
heapq.heappush(heap, 1)
heapq.heappush(heap, 7)
heapq.heappush(heap, 3)

print(heap)  # 输出：[1, 3, 7, 4]

# 弹出最小元素
smallest = heapq.heappop(heap)
print(smallest)  # 输出：1
print(heap)  # 输出：[3, 4, 7]

# 将列表转换为堆
list = [4, 6, 8, 1, 2, 9]
heapq.heapify(list)
print(list)  # 输出：[1, 2, 8, 4, 6, 9]

# 获取最大的3个元素
print(heapq.nlargest(3, list))  # 输出：[9, 8, 6]

# 获取最小的3个元素
print(heapq.nsmallest(3, list))  # 输出：[1, 2, 4]

6.4. 使用 heapq 实现最大堆

由于 heapq 默认实现的是最小堆，如果需要最大堆，可以通过以下方式来实现

import heapq

# 使用 heapq 实现最大堆
class MaxHeap:
    def __init__(self):
        self.heap = []

    def push(self, val):
        heapq.heappush(self.heap, -val)

    def pop(self):
        # heapq 默认实现的是最小堆，所以取相反数
        return -heapq.heappop(self.heap)

    def peek(self):
        # 三元表达式，如果 heap 不为空，返回 heap[0]，否则返回 None
        # 格式为：value_if_true if condition else value_if_false
        # 格式为：为真时的返回值 if 判定条件 else 为假时的返回值
        # return -self.heap[0] if self.heap else None
        if self.heap:
            return -self.heap[0]
        else:
            return None

    def size(self):
        return len(self.heap)

# 使用示例
max_heap = MaxHeap()
max_heap.push(3)
max_heap.push(1)
max_heap.push(4)
max_heap.push(2)

print(max_heap.pop())  # 输出: 4
print(max_heap.pop())  # 输出: 3
print(max_heap.peek())  # 输出: 2

7. 实现一个小顶堆：JavaScript 描述

使用数组来存储，因为二叉堆是个完全二叉树，如下tu：

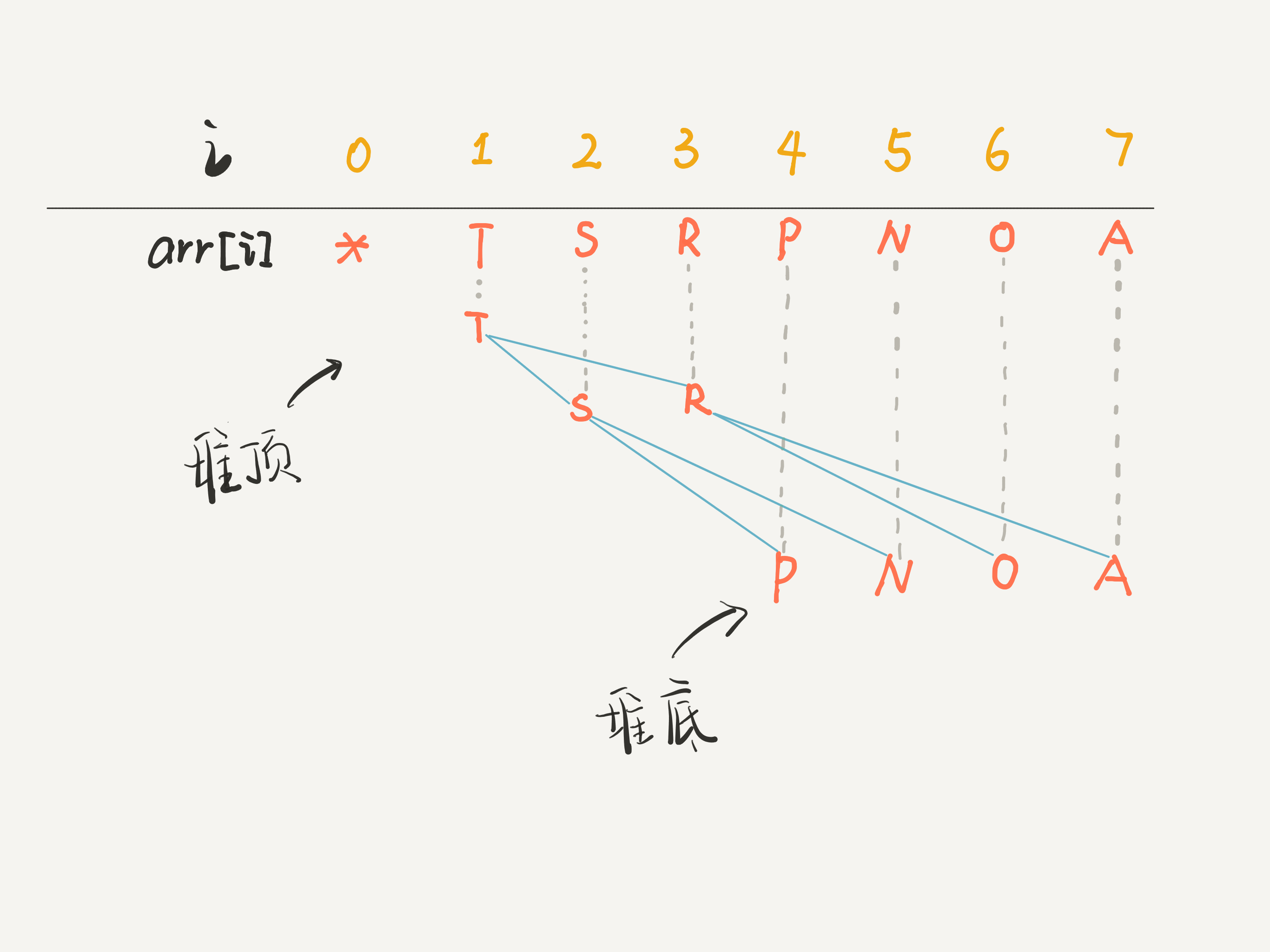
[!danger] 注意下面代码的高亮部分

function swap(array, a, b) {
  [array[a], array[b]] = [array[b], array[a]];
}

class MinHeap {
  constructor() {
    // 使用数组来存储
    this.heap = [];
  }

  // 获取左孩子的索引
  getLeftIndex(index) {
    return 2 * index + 1;
  }

  // 获取右孩子的索引
  getRightIndex(index) {
    return 2 * index + 2;
  }

  // 父节点的索引
  getParentIndex(index) {
    if (index === 0) {
      return 0;
    }
    return Math.floor((index - 1) / 2);
  }

  // 返回个数
  size() {
    return this.heap.length;
  }

  isEmpty() {
    return this.size() <= 0;
  }

  clear() {
    this.heap = [];
  }

  // ::::小顶堆，最小的肯定在最上面
  findMinimum() {
    return this.isEmpty() ? null : this.heap[0];
  }

  // 插入一个值，插入的元素添加到堆底的最后，然后让其上浮到正确位置（如果大顶的话）
  insert(value) {
    if (value != null) {
      const index = this.heap.length;
      // 先放在最后一位
      this.heap.push(value);
      // 向上移动，直到父节点小于插入的值
      this.shiftUp(index);
      return true;
    }
    return false;
  }

  /**
   * @description 下沉，堆化，递归
   * @param {number} index, 插入的元素的位置, 这个位置是指 数组的索引
   */
  shiftDown(index) {
    // 插入的元素的位置
    let pos = index;
    const left = this.getLeftIndex(index);
    const right = this.getRightIndex(index);
    const size = this.size();

    if (
      left < size && // 如果左子节点小于数组的长度，说明有左子节点
      this.heap[pos] > this.heap[left] // 如果该元素大于它的左子节点，则下沉，即 pos = left
    ) {
      pos = left;
    }

    if (
      right < size && // 如果右子节点小于数组的长度，说明有右子节点
      this.heap[pos] > this.heap[right] // 如果该元素大于它的右子节点，则下沉
    ) {
      pos = right;
    }

    // 如果 pos 最后 和传入的index不一样了，说明需要交换数据，然后继续下沉递归
    if (index !== pos) {
      swap(this.heap, index, pos);
      this.shiftDown(pos);
    }
  }

  /**
   * @description 上浮，堆化，递归:向上移动，直到父节点的值小于插入的值
   * @param {number} index, 插入的元素的位置, 这个位置是指 数组的索引
   */
  shiftUp(index) {
    let parentIndex = this.getParentIndex(index);
    while (
      index > 0 && // index必须大于0，因为根节点的父节点是自己
      this.heap[parentIndex] > this.heap[index] // 父节点的元素大于子元素的时候，才需要移动
    ) {
      swap(this.heap, parentIndex, index);

      // 交换后，继续向上移动
      index = parentIndex;
      parentIndex = this.getParentIndex(index);

      // 以下是错误的写法 需要注意，因为这是在 while 循环中，所以不需要递归,被递归影响了
      // 这是 while 循环，不是递归
      // 这是 while 循环，不是递归
      // // 交换后，继续向上移动，传入的index变成了父节点的索引
      // this.getParentIndex(parentIndex);
    }
  }

  // delete min 堆顶元素（最小值）和 堆底元素 对调
  // 1、删除删除堆顶元素
  // 2、让堆底元素替换到堆顶
  // 3、然后从堆顶开始下沉
  deleteMin() {
    if (this.isEmpty()) {
      return null;
    }
    if (this.size() === 1) {
      return this.heap.shift();
    }
    const removedValue = this.heap[0]; // 堆顶元素
    const lastElement = this.heap.pop(); // 移除堆底元素
    this.heap[0] = lastElement; // 将 堆顶元素 赋值为 堆底元素
    // 从堆顶开始下沉
    this.shiftDown(0);
    return removedValue;
  }

  getAsArray() {
    return this.heap;
  }
}

let arr = [5, 3, 7, 9, 0, 0, -1, -2, 7, -8];

let heapObj = new MinHeap();
arr.forEach((item) => {
  heapObj.insert(item);
});
console.log(heapObj);
console.log("************************");

console.log(heapObj.findMinimum());

堆的使用场景

优先队列：堆通常作为实现优先队列的首选数据结构，其入队和出队操作的时间复杂度均为 O(log⁡n) ，而建堆操作为 O(n) ，这些操作都非常高效。
堆排序：给定一组数据，我们可以用它们建立一个堆，然后不断地执行元素出堆操作，从而得到有序数据。然而，我们通常会使用一种更优雅的方式实现堆排序，详见“堆排序”章节。
获取最大的 k 个元素：这是一个经典的算法问题，同时也是一种典型应用，例如选择热度前 10 的新闻作为微博热搜，选取销量前 10 的商品等。

liguwe's site

二叉堆

目录