二叉树的层次遍历与 BFS 算法
目录
4. 最大层内元素和

/**
* @param {TreeNode} root
* @return {number}
*/
var maxLevelSum = function (root) {
// ::::::::如果根节点为空,直接返回0
if (root === null) {
return 0;
}
// ::::::::层次
let depth = 1;
// ::::::::结果
let res = 0;
// ::::::::最大值,默认为最小值
// let maxSum = -100000;
let maxSum = -Infinity;
let q = [root];
while (q.length) {
let size = q.length;
let levelSum = 0;
for (let i = 0; i < size; i++) {
// ::::::::出队列,注意,这个是在 for 循环中的
const node = q.shift();
levelSum += node.val
if (node.left !== null) {
q.push(node.left)
}
if (node.right !== null) {
q.push(node.right);
}
}
if (levelSum > maxSum) {
res = depth;
maxSum = levelSum;
}
depth++;
}
return res;
};
- 一个技巧:如果忘了
-Infinity,则可以直接写成题设中的最小值,是10000 const node = q.shift();是在for 循环里面
5. N 叉树的层序遍历

/**
* @param {Node|null} root
* @return {number[][]}
*/
var levelOrder = function (root) {
// ::::::::如果根节点为空,则返回空数组
if (root === null) {
return [];
}
// ::::::::返回的结果
let res = [];
// ::::::::辅助队列,初始化队列,首先加入根节点
let q = [root];
/**
* ::::::::层次遍历框架:队列不为空时,循环
**/
while (q.length) {
// ::::::::用于存储当前层的节点值
let level = [];
let size = q.length;
for (let i = 0; i < size; i++) {
// ::::::::出队列
const node = q.shift();
level.push(node.val);
// ::::::::遍历子节点,入队列,多叉树的子节点是一个数组
for (let item of node.children) {
q.push(item);
}
}
res.push(level);
}
return res;
};
两个要点:
- 层次遍历的框架,一定无误的默写出来
- 多叉树,比二叉树,只是从
node.left 和 node.right变成了node.children而已
6. 递归的方式实现层序遍历
var levelTraverse = function (root) {
let res = [];
// ::::关键是把 depth、res 作为参数传入
traverse(root, 0, res);
return res;
};
/**
* @description 递归遍历
* @param {TreeNode} root
* @param {number} depth
* @param {number[][]} res
* */
function traverse(root, depth, res) {
if (root == null) {
return;
}
// 前序位置,看看是否已经存储 depth 层的节点了
if (res.length <= depth) {
// 第一次进入 depth 层
res.push([]);
}
// 前序位置,在 depth 层添加 root 节点的值
res[depth].push(root.val);
traverse(root.left, depth + 1, res);
traverse(root.right, depth + 1, res);
}
- 这种思路从结果上说确实可以得到层序遍历结果,
- 但其
本质还是二叉树的前序遍历,或者说 DFS 的思路,而不是层序遍历,或者说 BFS 的思路 因为这个解法是依赖前序遍历自顶向下、自左向右的顺序特点得到了正确的结果。
- 但其
- 抽象点说,这个解法更像是从左到右的「列序遍历」,而不是自顶向下的「层序遍历」。
- 所以对于计算最小距离的场景,这个解法完全等同于 DFS 算法,没有 BFS 算法的性能的优势。
7. 扩散 到 BFS算法:岛屿数量
- 其实,
层次遍历扩散后就是BFS算法- 二叉树的
层次遍历是:for循环中扩散左右子节点 - 多叉树的
层次遍历是:for循环中扩散children子节点 - 岛屿问题的
层次遍历是:for循环中扩散上下左右节点,如下图:
- 二叉树的
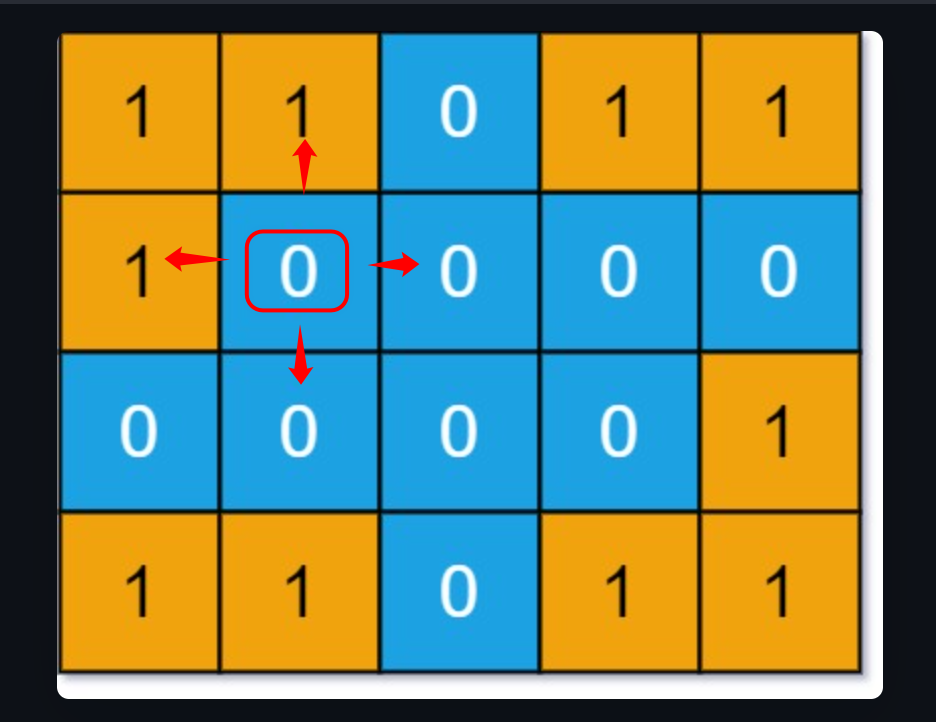

/**
* @param {character[][]} grid
* @return {number}
*/
var numIslands = function (grid) {
let res = 0;
// ::::::::行数
const m = grid.length;
if (m === 0) {
return res;
}
// ::::::::列数
const n = grid[0].length;
// ::::::::遍历整个二维数组
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
// ::::::::如果当前位置是岛屿
if (grid[i][j] === '1') {
// ::::::::岛屿数量加一
res++;
//:::: 然后使用 DFS 将岛屿淹了
bfs(grid, i, j);
}
}
}
return res;
};
/**
* @description ::::从 (i, j) 开始,将与之相邻的陆地都变成海水
* */
var bfs = function (grid, i, j) {
// ::::::::行数
const m = grid.length;
// ::::::::列数
const n = grid[0].length;
// ::::::::辅助队列,初始化队列,首先加入根节点
const q = [i, j](/post/LpbspKpp.html#i,-j);
// :::: 将当前位置的值置标识为 0,即将岛屿淹了
grid[i][j] = '0';
while (q.length) {
let size = q.length;
for (let k = 0; k < size; k++) {
const [x, y] = q.shift();
// ::::上边,如果上边是陆地,则入队列,并且将陆地变成海水
if (y - 1 >= 0 && grid[x][y - 1] === '1') {
q.push([x, y - 1]);
grid[x][y - 1] = '0';
}
// 下边,如果下边是陆地,则入队列,并且将陆地变成海水
if (y + 1 < n && grid[x][y + 1] === '1') {
q.push([x, y + 1]);
grid[x][y + 1] = '0';
}
// 左边,如果左边是陆地,则入队列,并且将陆地变成海水
if (x - 1 >= 0 && grid[x - 1][y] === '1') {
q.push([x - 1, y]);
grid[x - 1][y] = '0';
}
// 右边,如果右边是陆地,则入队列,并且将陆地变成海水
if (x + 1 < m && grid[x + 1][y] === '1') {
q.push([x + 1, y]);
grid[x + 1][y] = '0';
}
}
}
}
当然,这个题还有
DFS 解法,后文会提到
8. 总结
- 很多网格,二维数组类(如岛屿问题)题目可以使用这种
层次遍历框架 - 很多最小值问题,智力最小值问题等可以考虑使用
层次遍历框架 - 请务必牢记
层次遍历框架,记着了框架这些题都能写出来 层次遍历框架及BFS 算法的关系是什么,请回答?- 层次遍历继承了BFS的核心思想,但更专注于树的特定需求
- 层次遍历通常不需要visited集合,因为树没有环
- 层次遍历常常需要记录层次信息,而普通BFS不需要
- 层次遍历是BFS在树结构上的特化版本
- 两者都基于队列实现,保证了从近到远的访问顺序