链表：Python 描述

#数据结构/链表 #数据结构

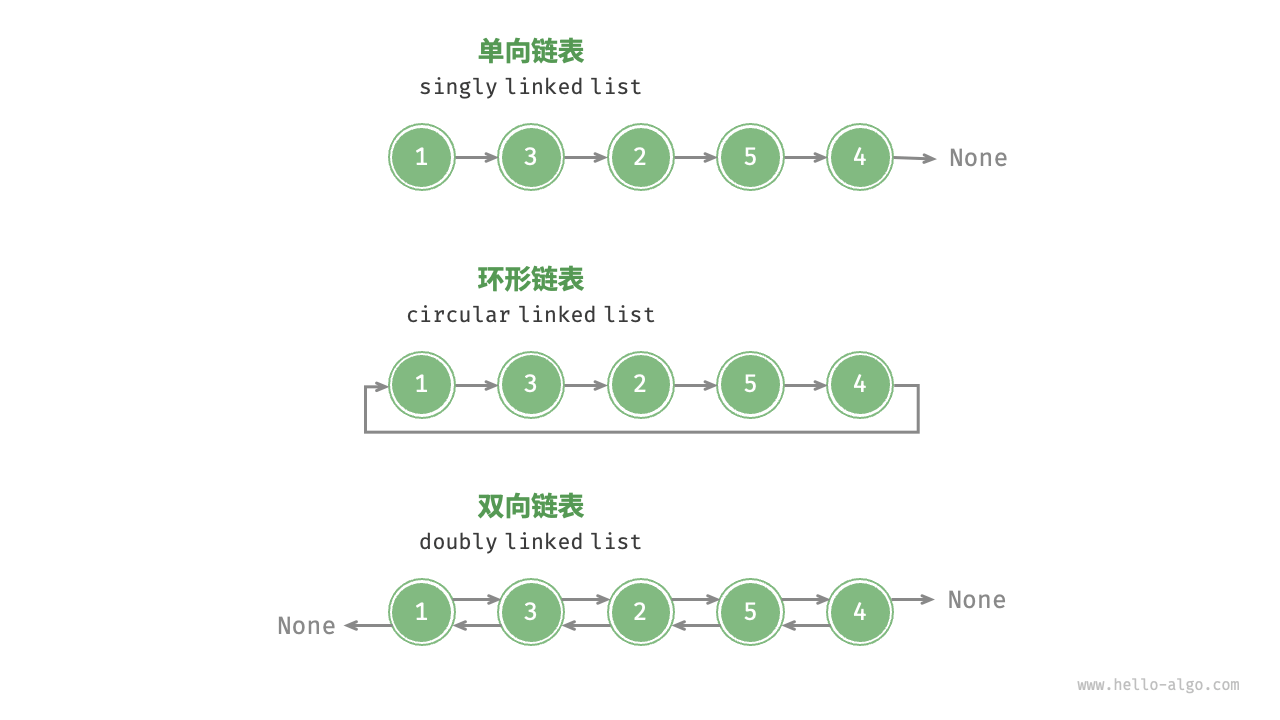
1. 链表的分类

单链表
环形链表
双向链表

2. 链表的存储是分散的

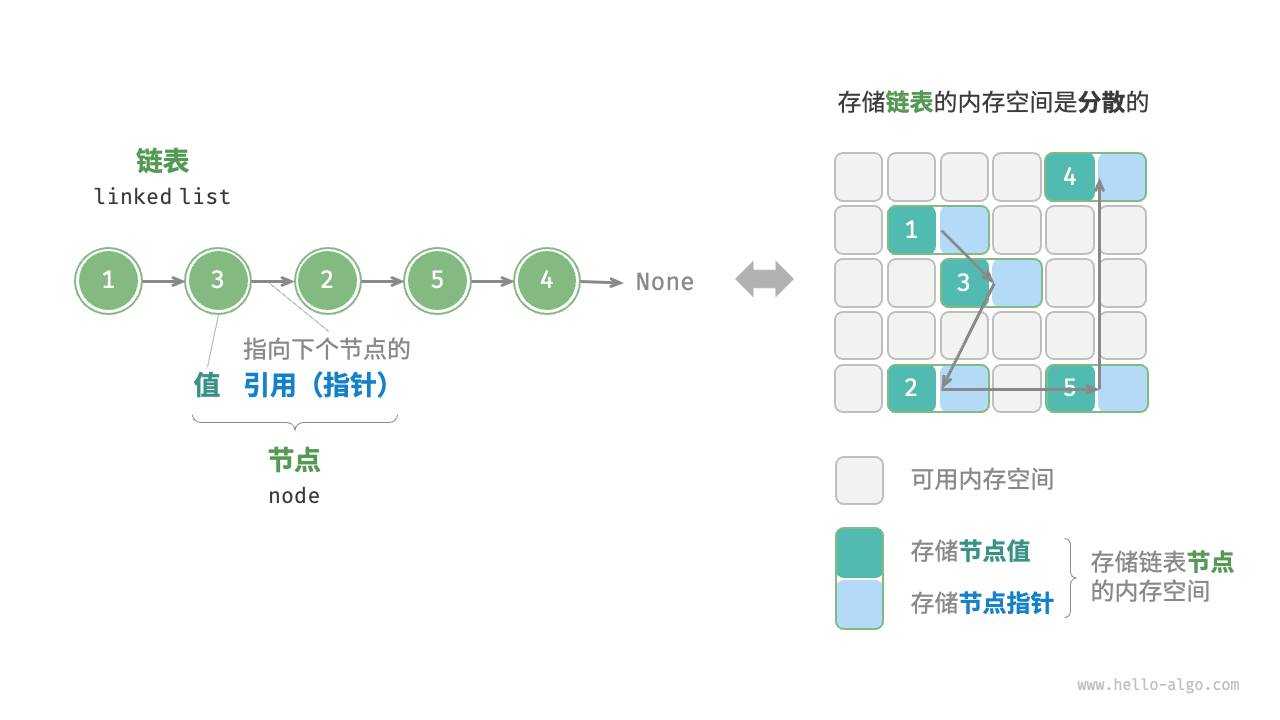
尾节点指向的是空

JS 中被记为 null
Python 中分别被记为 None

3. 链表的好处

不需要考虑扩缩容和数据搬移的问题，用的时候就能接上，不用的时候拆掉就行了
所以，比数组要节省内存

4. 单链表节点的增删改查

class ListNode:
    def __init__(self,val:int) -> None:
        # 节点值
        self.val = val
        # listNode | Node 代表 self.next 的值可能是 listNode | Node
        self.next:ListNode | None = None

4.1. 初始化

n0 = ListNode(0)
n1 = ListNode(1)
n2 = ListNode(2)
n3 = ListNode(3)
n4 = ListNode(4)

n0.next = n1
n1.next = n2
n2.next = n3
n3.next = n4
# 最后一个节点的 next 指向 None
n4.next = None

4.2. 单链表的遍历：查或改

############################################
# 单链表的遍历：查或改
############################################
p = n0
val = 2
while p is not None:
    print(p.val)
    if p.val == val:
        ## 修改为 20
        p.val = 20
    p = p.next

4.3. 单链表的插入

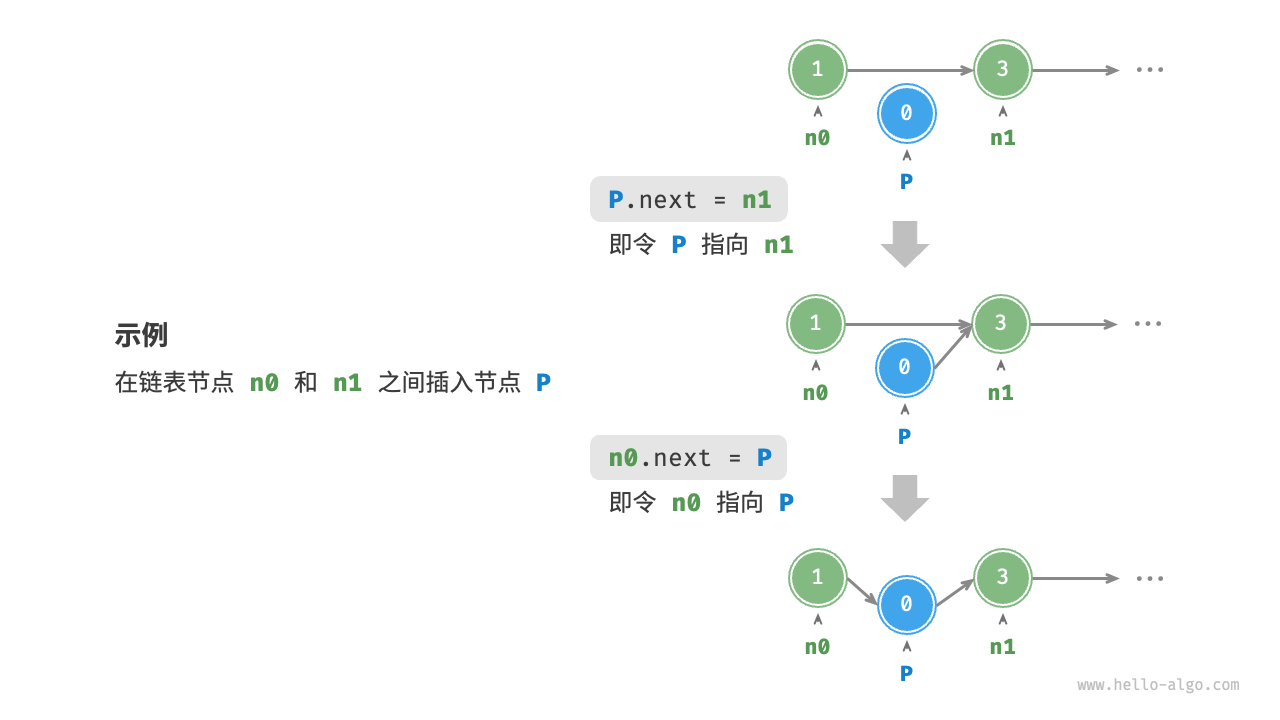
4.3.1. 头部插入

####### 头部插入
p = n0
n5 = ListNode(5)
n5.next = p
# 变成了 n5 -> n0 -> n1 -> n2 -> n3 -> n4
# 即 5 -> 0 -> 1 -> 2 -> 3 -> 4

4.3.2. 尾部插入

###### 尾部插入
p = n0
n5 = ListNode(5)
while p.next is not None:
    p = p.next
p.next = n5
# 变成了 n0 -> n1 -> n2 -> n3 -> n4 -> n5
# 即 0 -> 1 -> 2 -> 3 -> 4 -> 5

4.3.3. 中间插入

###### 中间插入
# 需要插入的节点
n5 = ListNode(5)
# 需要插入的位置
pos = 2
# 头结点
p = n0
while pos > 0 and p.next is not None:
    p = p.next
    pos -= 1

# 将 n5 的 next 指向 p 的 next
n5.next = p.next
# 将 n5 插入到 p 的后面
p.next = n5

4.4. 单链表的删除

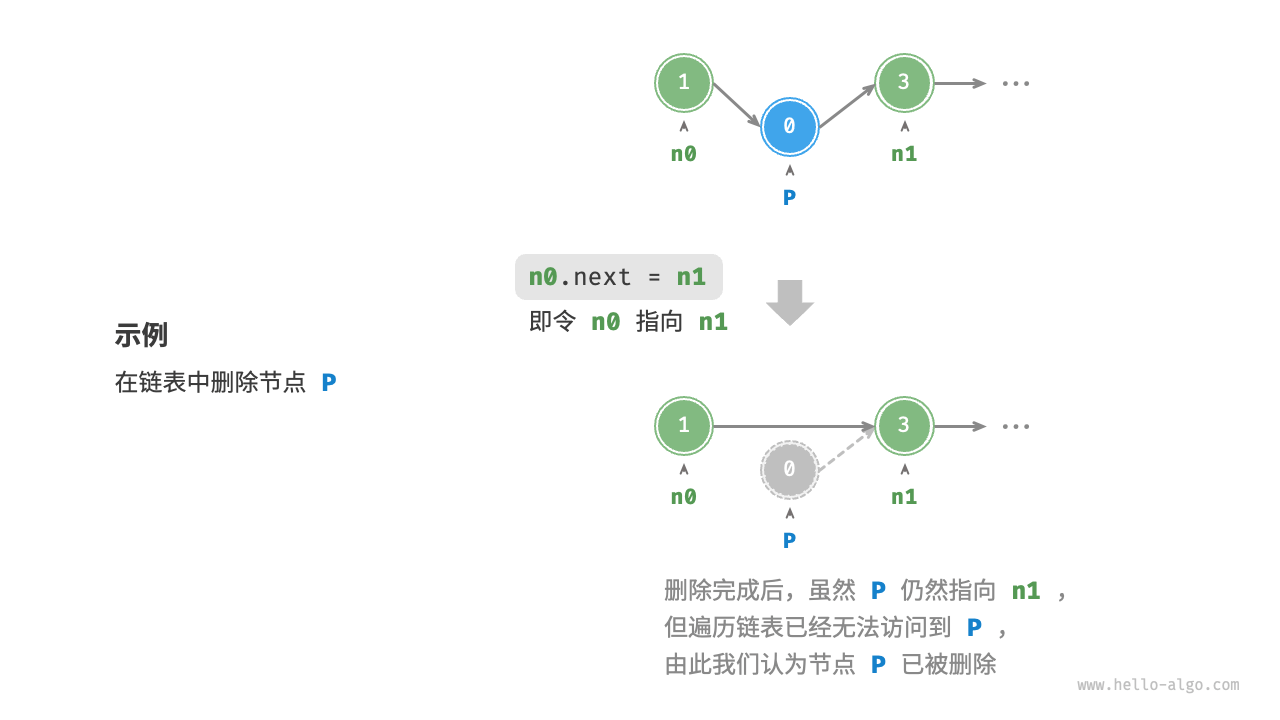
# 需要删除的节点的值
val = 2
# 头结点
p = n0
# 删的第一步是查
# 查找到需要删除的节点的前一个节点
while p.next is not None:
    # 如果下一个节点的值等于 val，将下一个节点删除
    if p.next.val == val:
        p.next = p.next.next
    else:
        p = p.next

5. 双向链表节点的增删改成

# 双链表节点
class Node:
    def __init__(self, prev, val:int, next) -> None:
        # 节点值
        self.val = val
        # 前一个节点
        self.prev = prev
        # 后一个节点
        self.next = next

5.1. 初始化

# 创建双链表
n0 = Node(None, 0, None)
n1 = Node(n0, 1, None)
n2 = Node(n1, 2, None)
n3 = Node(n2, 3, None)

# 连接双链表
# n0 -> n1 -> n2 -> n3
n0.next = n1
n1.next = n2
n2.next = n3
n3.next = None
# n0 <- n1 <- n2 <- n3
n3.prev = n2
n2.prev = n1
n1.prev = n0
n0.prev = None

# 最终
# Node <- n0 <-> n1 <-> n2 <-> n3 -> None

5.2. 遍历

############################################
# 双链表的查：遍历
# ############################################

# 向后遍历
p = n0
while p is not None:
    p = p.next
    print(p.val)

# 向前遍历
p = n3
while p is not None:
    p = p.prev
    print(p.val)

5.3. 插入

############################################
# 双链表的插入:插
# ############################################

# 需要插入的节点
n4 = Node(None, 4, None)
# 需要插入的位置
pos = 2
# 头结点
p = n0

# 查找到需要插入的位置
while pos > 0 and p.next is not None:
    pos -= 1
    p = p.next

# 将 n5 的 prev 指向 p
n4.prev = p
# 将 n5 的 next 指向 p 的 next
n4.next = p.next

5.4. 删除

############################################
# 双链表的删除
# ############################################

# 需要删除的节点
del_node = n2
# 将 n2 的前一个节点的 next 指向 n2 的下一个节点
del_node.prev.next = del_node.next
# 将 n2 的下一个节点的 prev 指向 n2 的前一个节点
del_node.next.prev = del_node.prev

6. 链表的使用场景

6.1. 单向链表

单向链表通常用于实现栈、队列、哈希表和图等数据结构。

栈与队列：
- 当插入和删除操作都在链表的一端进行时，它表现的特性为先进后出，对应栈；
- 当插入操作在链表的一端进行，删除操作在链表的另一端进行，它表现的特性为先进先出，对应队列。
哈希表：链式地址是解决哈希冲突的主流方案之一，在该方案中，所有冲突的元素都会被放到一个链表中。
图：邻接表是表示图的一种常用方式，其中图的每个顶点都与一个链表相关联，链表中的每个元素都代表与该顶点相连的其他顶点。

6.2. 双向链表

双向链表常用于需要快速查找前一个和后一个元素的场景。

高级数据结构：比如在红黑树、B 树中，我们需要访问节点的父节点，这可以通过在节点中保存一个指向父节点的引用来实现，类似于双向链表。
浏览器历史：在网页浏览器中，当用户点击前进或后退按钮时，浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。
LRU 算法：在缓存淘汰（LRU）算法中，我们需要快速找到最近最少使用的数据，以及支持快速添加和删除节点。这时候使用双向链表就非常合适。

6.3. 环形链表

环形链表常用于需要周期性操作的场景，比如操作系统的资源调度。

时间片轮转调度算法：在操作系统中，时间片轮转调度算法是一种常见的 CPU 调度算法，它需要对一组进程进行循环。每个进程被赋予一个时间片，当时间片用完时，CPU 将切换到下一个进程。这种循环操作可以通过环形链表来实现。
数据缓冲区：在某些数据缓冲区的实现中，也可能会使用环形链表。比如在音频、视频播放器中，数据流可能会被分成多个缓冲块并放入一个环形链表，以便实现无缝播放。

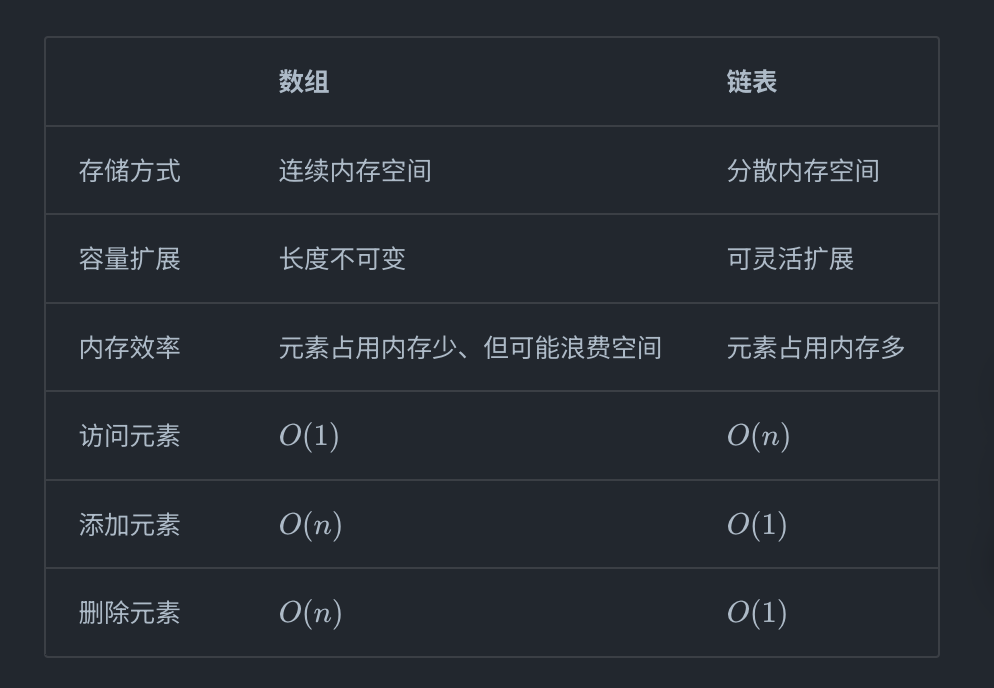
7. 数组和链表的对比

8. 技巧：虚拟头结点 & 虚拟尾节点

我们会使用「虚拟头结点」技巧，把头、尾、中部的操作统一起来，同时还能避免处理头尾指针为空情况的边界情况

8.1. 虚拟头尾节点技巧原理

它的原理很简单，就是在创建双链表时就创建一个虚拟头节点和一个虚拟尾节点，无论双链表是否为空，这两个节点都存在。这样就不会出现空指针的问题，可以避免很多边界情况的处理

8.2. 示例：双链表

举例来说，假设虚拟头尾节点分别是 dummyHead 和 dummyTail，那么一条空的双链表长这样：

dummyHead <-> dummyTail

如果你添加 1,2,3 几个元素，那么链表长这样：

dummyHead <-> 1 <-> 2 <-> 3 <-> dummyTail

你以前要把在头部插入元素、在尾部插入元素和在中间插入元素几种情况分开讨论，现在有了头尾虚拟节点，无论链表是否为空，都只需要考虑在中间插入元素的情况就可以了，这样代码会简洁很多。

8.3. 示例：单链表

举例来说，假设虚拟头尾节点分别是 dummyHead 和 dummyTail，那么一条空的单链表长这样：

dummyHead -> dummyTail