回溯算法与DFS算法的区别

#DFS #回溯算法

目录

• 1. 树枝与节点的区别
• 2. 算法框架区别
• 3. backtrack、dfs、traverse ==不要有返回值==
• 4. traverse 的 base case ==写在前面==
• 5. backtrack 的 base case ==写在前面==
• 6. 回溯算法的==剪枝逻辑==写在哪儿？

1. 树枝与节点的区别

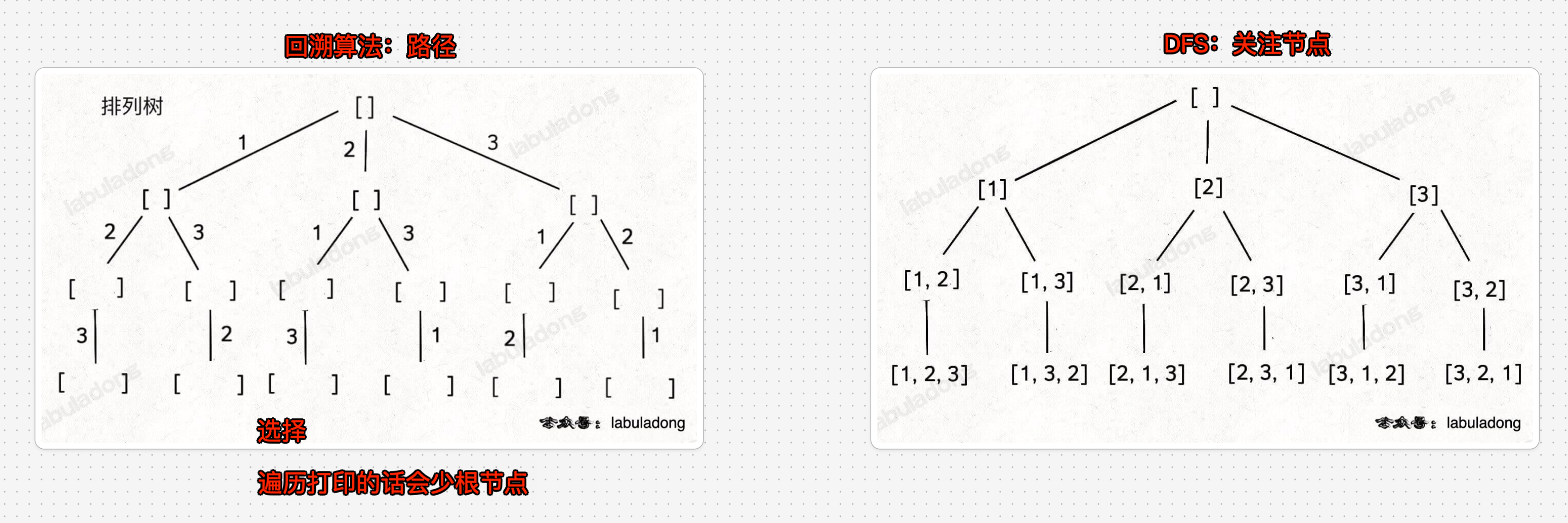
• 其实回溯算法和我们常说的 DFS 算法非常类似，本质上就是一种暴力穷举算法
  • 回溯算法 和 DFS 算法的细微差别是：
    • 回溯算法是在遍历「树枝」 ，在于路径
    • DFS 算法是在遍历「节点」

2. 算法框架区别

• 做选择和撤销选择==是否在 for 循环里面==

// 回溯算法框架模板
function backtrack(...) {
    if (到达叶子节点) {
        return;
    }
    for (int i = 0; i < n; i++;) {
        // 做选择
        ...
        backtrack(...)
        // 撤销选择
        ...
    }
}

// DFS 算法框架模板
function dfs(...) {
    if (到达叶子节点) {
        return;
    }
    // 做选择
    ...
    for (int i = 0; i < n; i++) {
        dfs(...)
    }
    // 撤销选择
    ...
}

3. backtrack、dfs、traverse ==不要有返回值==

• 对于 backtrack/dfs/traverse 函数，就作为单纯的遍历函数，==请不要给它们带返回值==
  • 因为这是遍历的思路
    • 而分解问题的思路，则一定会有返回值
• 如果需要其他变量，请使用外部变量

4. traverse 的 base case ==写在前面==

void traverse(TreeNode root) {
    // base case
    if (root == null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

5. backtrack 的 base case ==写在前面==

void backtrack(...) {
    // base case
    if (到达叶子节点) {
        return;
    }

    for (int i = 0, i < n; i++) {
        // 剪枝逻辑
        if (第 i 个选择不满足条件) {
            continue;
        }

        // 做选择
        ...

        backtrack(...)

        // 撤销选择
        ...
    }
}

6. 回溯算法的==剪枝逻辑==写在哪儿？

注意是 continue

void backtrack(...) {
    // base case
    if (到达叶子节点) {
        return;
    }

    for (int i = 0, i < n; i++) {
        // 剪枝逻辑
        if (第 i 个选择不满足条件) {
            continue;
        }

        // 做选择
        ...

        backtrack(...)

        // 撤销选择
        ...
    }
}