快速排序算法的原理及运用
#算法/快排 #2024/09/16 #算法/排序
目录
1. 快排算法
1.1. 一句话总结快排算法
快速排序是先将一个元素排好序,然后再将剩下的元素排好序
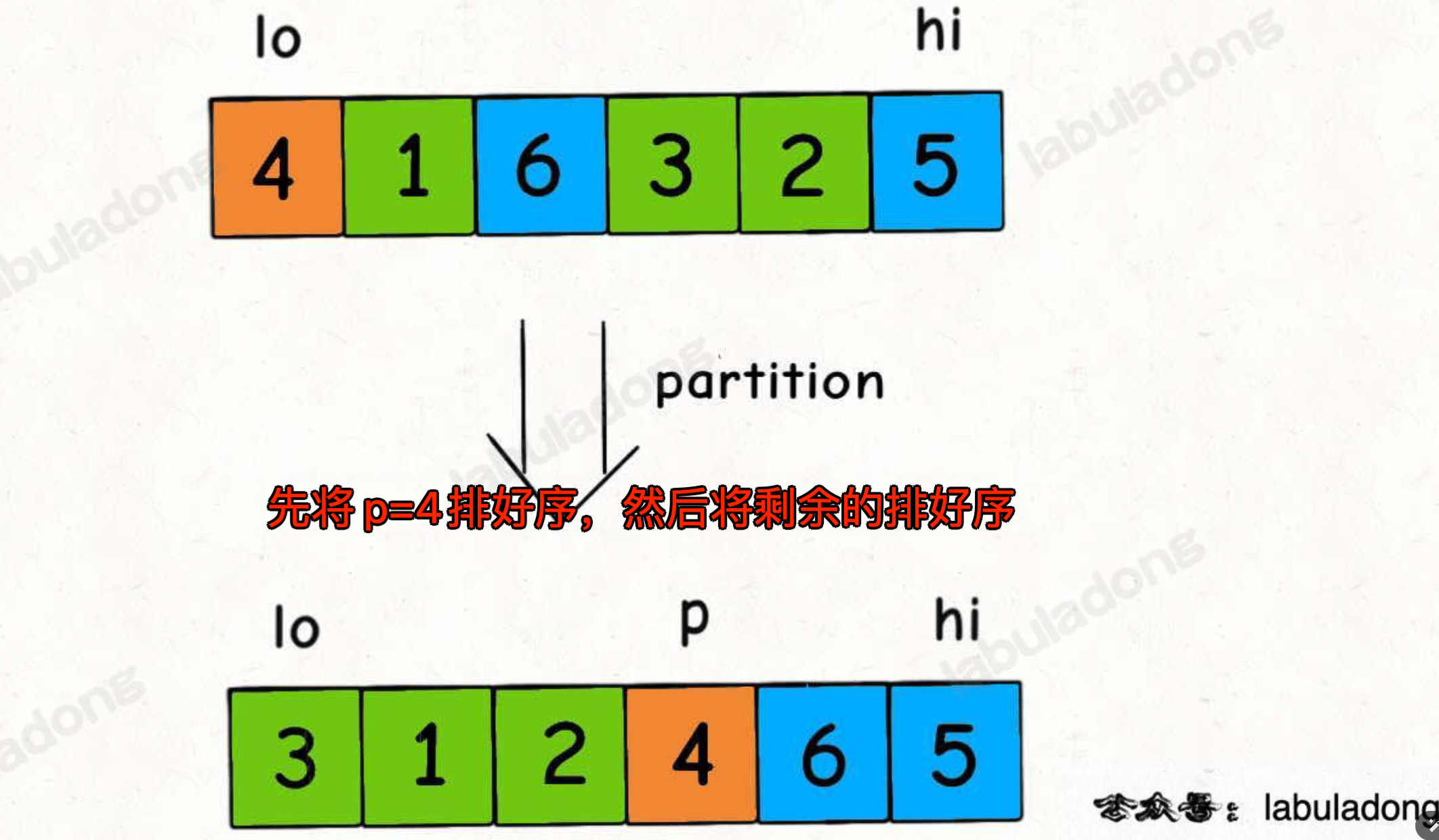
这就像是在整理一大堆杂乱的物品,我们先选一个标准,把物品分成两堆,然后再分别整理这两堆,如此反复,最终就能得到一个井然有序的结果。
1.2. 快排就是构造 BST 的过程

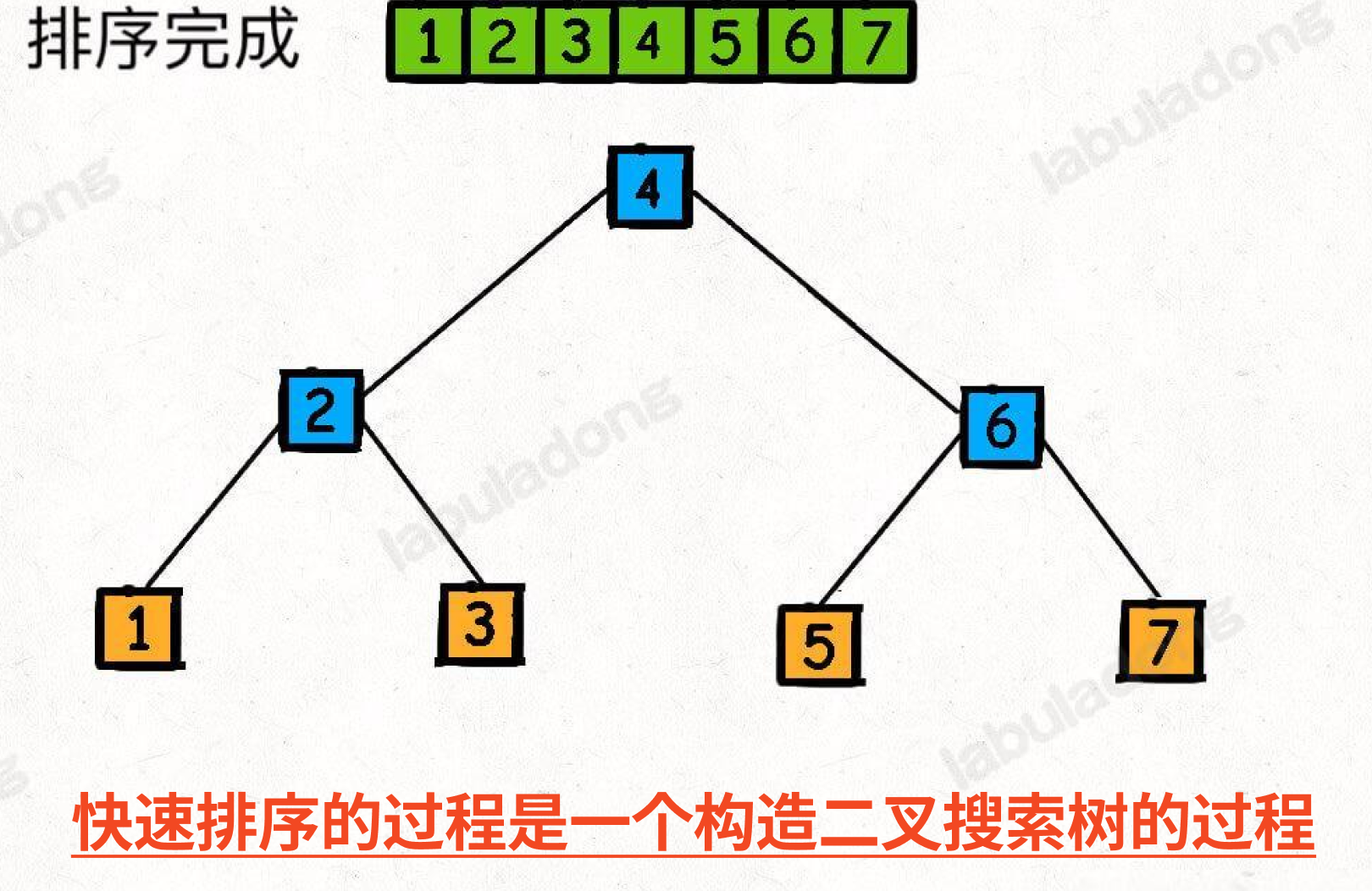
一种极端场景:你不可能每次都选中了合适的切分点吧,比如上图中的 4 ,所以如果有一边的元素特别少的话,会导致二叉树生长不平衡,如下图:
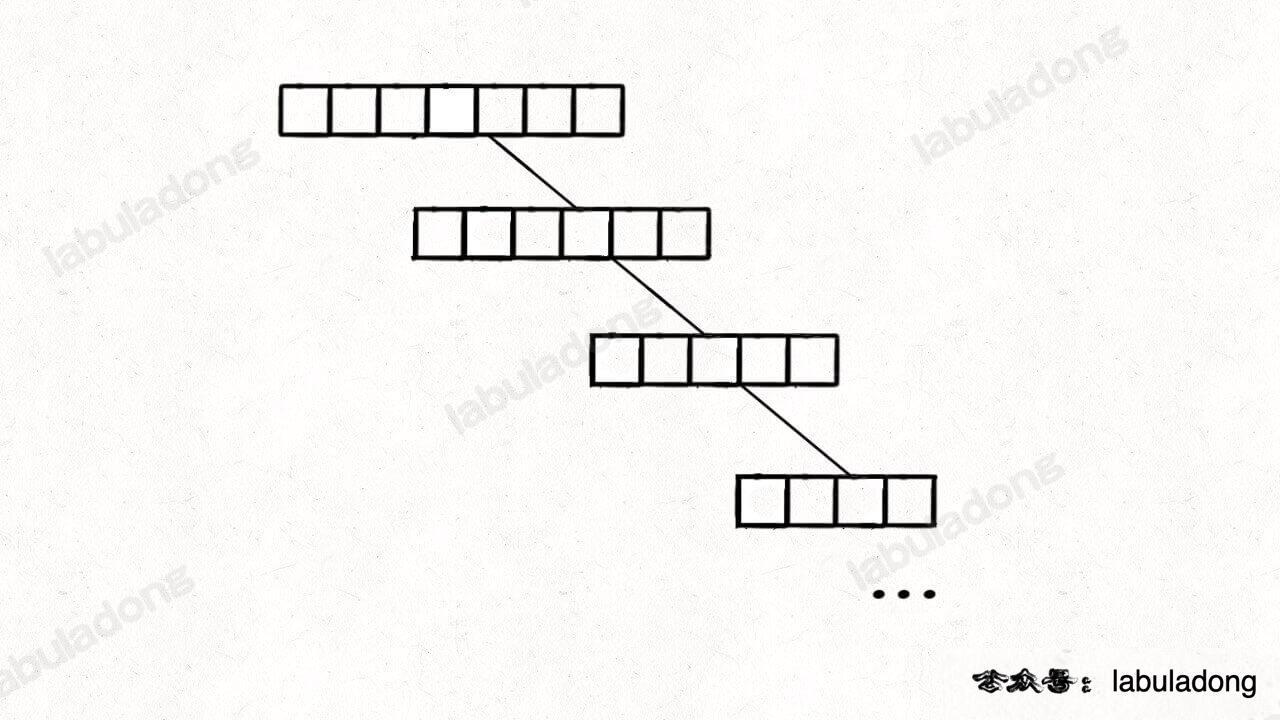
所以需要随机性,两种方法
- 洗牌数组
- 随机选中切分点
经过随机化的
partition函数很难出现极端情况
1.3. 快排与二叉树的遍历的关系
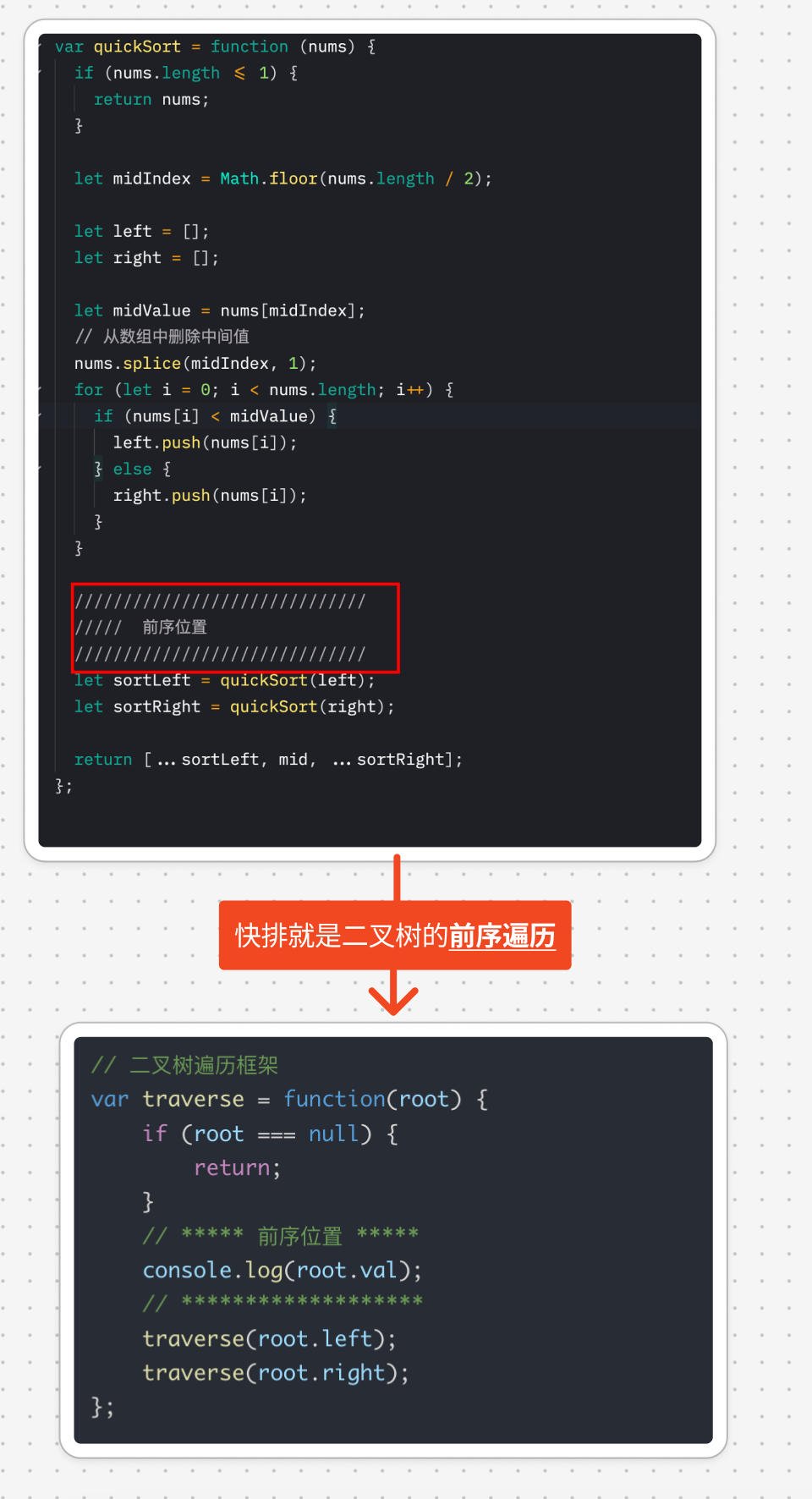
1.4. 代码实现一:简单实现
var quickSort = function (nums) {
if (nums.length <= 1) {
return nums;
}
let midIndex = Math.floor(nums.length / 2);
let left = [];
let right = [];
let mid = [];
let midValue = nums[midIndex];
// 从数组中删除中间值
nums.splice(midIndex, 1);
for (let i = 0; i < nums.length; i++) {
if (nums[i] < midValue) {
left.push(nums[i]);
} else if (nums[i] > midValue) {
right.push(nums[i]);
} else {
mid.push(nums[i]);
}
}
//**********************
// 前序位置
//**********************
let sortLeft = quickSort(left);
let sortRight = quickSort(right);
return [...sortLeft, ...mid, ...sortRight];
};
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var findKthLargest = function (nums, k) {
let sorted = quickSort(nums);
return sorted[sorted.length - k];
};
1.4.1. 复杂度分析
- 时间复杂度:
- 快速排序的平均时间复杂度是 O(n log n),其中 n 是数组的长度。
- 最坏情况下(当数组已经排序或者接近排序时),时间复杂度可能退化到 O(n^2)。
- 最坏情况时间复杂度:O(n^2)
- 总的平均时间复杂度:O(n log n)
- 空间复杂度:
- 快速排序的空间复杂度主要来自递归调用栈和创建的新数组。
- 平均情况下,递归深度为 O(log n)。
- 每次递归都创建了新的 left、right 和 mid 数组,最坏情况下可能需要
O(n)的额外空间。 - 总的空间复杂度:O(n log n)
- 最坏情况空间复杂度:O(n^2)
- 额外说明:
- 这个实现使用了额外的数组空间,而不是原地排序,这增加了空间复杂度。
- 对于找第k大元素的问题,其实不需要完全排序数组,可以使用快速选择算法(QuickSelect)来优化,使平均时间复杂度降低到 O(n)。
- 优化建议:
- 可以考虑使用原地快速排序来减少空间使用。
1.5. 代码实现二:原地排序
[!danger] 说实话,完全写出来还是挺难的,掌握原理就行了,能够写出来成本收益又如何呢?
var quickSort = function (nums) {
// 为了避免出现耗时的极端情况,先随机打乱
shuffle(nums);
// 排序整个数组(原地修改)
sort(nums, 0, nums.length - 1);
};
// 洗牌算法,将输入的数组随机打乱
var shuffle = function (nums) {
for (let i = nums.length - 1; i > 0; i--) {
const j = Math.floor(Math.random() * (i + 1));
// ES6 的解构赋值
[nums[i], nums[j]] = [nums[j], nums[i]];
}
};
var sort = function (nums, lo, hi) {
// 递归的终止条件, lo >= hi 时返回
if (lo >= hi) {
return;
}
// 对 nums[lo..hi] 进行切分
// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
var p = partition(nums, lo, hi);
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
};
/**
*@description 对数组 nums 的子区间 [lo, hi] 进行切分操作
* 从[lo,hi]中x选择 pivot = nums[lo] 作为切分点
* 将小于 pivot 的元素放在左侧,大于 pivot 的元素放在右侧
*@param {number[]} nums 待切分的数组
*@param {number} lo 切分的左边界
*@param {number} hi 切分的右边界
*@return {number} 返回 p, 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
*/
var partition = function (nums, lo, hi) {
var pivot = nums[lo];
var i = lo + 1, // i 从 lo + 1 开始,逐渐向右逼近
j = hi; // j 从 hi 开始,逐渐向左逼近
// 当 i > j 时结束循环,以保证区间 [lo, hi] 都被覆盖
while (i <= j) {
while (i < hi && nums[i] <= pivot) {
i++;
// 此 while 结束时恰好 nums[i] > pivot
}
while (j > lo && nums[j] > pivot) {
j--;
// 此 while 结束时恰好 nums[j] <= pivot
}
// 这个时候可以自己跳出循环了
if (i >= j) {
break;
}
// 此时 [lo, i) <= pivot && (j, hi] > pivot
// 交换 nums[j] 和 nums[i]
[nums[i], nums[j]] = [nums[j], nums[i]];
// 此时 [lo, i] <= pivot && [j, hi] > pivot
}
// 最后将 pivot 放到合适的位置,即 pivot 左边元素较小,右边元素较大
[nums[lo], nums[j]] = [nums[j], nums[lo]];
return j;
};
2. 快速选择算法
快速选择算法是一种用于找到数组中第k小(或第k大)元素的高效算法。它的思想源自于快速排序算法,但通常比完整的排序更快,因为它只需要部分排序数组。
让我们深入了解快速选择算法:
- 算法概述: 快速选择的主要思想是使用类似快速排序的分区策略,但只递归地搜索包含第k小元素的那一部分。
- 算法步骤: a. 选择一个基准元素(pivot) b. 将数组分区,使得小于基准的元素在左边,大于基准的元素在右边 c. 根据分区位置和k的关系,决定是返回结果,还是继续在左边或右边递归查找
- JavaScript 实现:
function quickSelect(arr, k) {
// k应该在1到arr.length之间
if (k < 1 || k > arr.length) {
return null;
}
return select(arr, 0, arr.length - 1, k);
}
function select(arr, left, right, k) {
// 如果左右指针相遇,说明找到了第k小的元素
if (left === right) {
return arr[left];
}
// 选择基准并分区
let pivotIndex = partition(arr, left, right);
// 计算基准的秩(即它是第几小的元素)
let rank = pivotIndex - left + 1;
if (k === rank) {
// 如果基准的秩正好是k,那么它就是第k小的元素
return arr[pivotIndex];
} else if (k < rank) {
// 如果k小于rank,在左半部分继续查找
return select(arr, left, pivotIndex - 1, k);
} else {
// 如果k大于rank,在右半部分继续查找
return select(arr, pivotIndex + 1, right, k - rank);
}
}
function partition(arr, left, right) {
let pivot = arr[right]; // 选择最右边的元素作为基准
let i = left - 1;
for (let j = left; j < right; j++) {
if (arr[j] <= pivot) {
i++;
[arr[i], arr[j]] = [arr[j], arr[i]]; // 交换元素
}
}
[arr[i + 1], arr[right]] = [arr[right], arr[i + 1]]; // 将基准放到正确的位置
return i + 1;
}
// 使用示例
let arr = [3, 2, 1, 5, 6, 4];
console.log(quickSelect(arr, 2)); // 输出:2(第2小的元素)
console.log(quickSelect(arr, 4)); // 输出:4(第4小的元素)
- 算法分析:
- 时间复杂度:
- 平均情况:O(n)
- 最坏情况:O(n²)(但这种情况很少发生,尤其是如果我们随机选择基准)
- 空间复杂度:O(1),因为它是原地操作的
- 时间复杂度:
- 优点:
- 在平均情况下,它比排序整个数组然后选择第k个元素要快得多
- 它是一个原地算法,不需要额外的空间
- 对于大型数据集寻找中位数或者其他百分位数非常有效
- 应用场景:
- 寻找数组中的中位数
- 寻找第k大(或第k小)的元素
- 解决 Top K 问题
- 在某些数据流算法中用于维护运行时的统计信息
- 优化:
- 使用随机选择基准可以进一步改善最坏情况的性能
- 对于小规模子数组,可以切换到插入排序等简单算法来提高效率
快速选择算法是一个强大而优雅的算法,它展示了如何通过只解决问题的一部分来高效地得到答案。理解和掌握这个算法不仅能帮助解决特定的问题,还能提供一种解决更广泛问题的思路。
3. 相关题目
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 215. Kth Largest Element in an Array | 215. 数组中的第K个最大元素 | 🟠 |
| 912. Sort an Array | 912. 排序数组 | 🟠 |
| - | 剑指 Offer II 076. 数组中的第 k 大的数字 | 🟠 |
4. 参考
https://labuladong.online/algo/practice-in-action/quick-sort/