二叉树的最大深度
目录
1. 遍历一遍的思路
重点:
- 前序位置代表进入一个节点,这个时候需要
depth++ - 后序位置代表进入一个节点,这个时候需要
depth--
var maxDepth = function (root) {
let res = 0;
let depth = 0;
function traverse(root) {
if (!root) {
return;
}
// 每进入一个节点时,更新下 res
depth++;
res = Math.max(res, depth);
traverse(root.left);
traverse(root.right);
// 离开节点时,更新下 res
depth--;
}
traverse(root);
return res;
};
2. 分解问题的思路
重点:
l和r直接简写吧,真正写题的时候,时间有限- ==原二叉树的最大深度 = 左右子树的最大深度的最大值 + 1==
var maxDepth = function (root) {
if (!root) {
return 0;
}
let l = maxDepth(root.left);
let r = maxDepth(root.right);
return 1 + Math.max(l, r);
};
3. 二叉树的最大深度
3.1. 题目
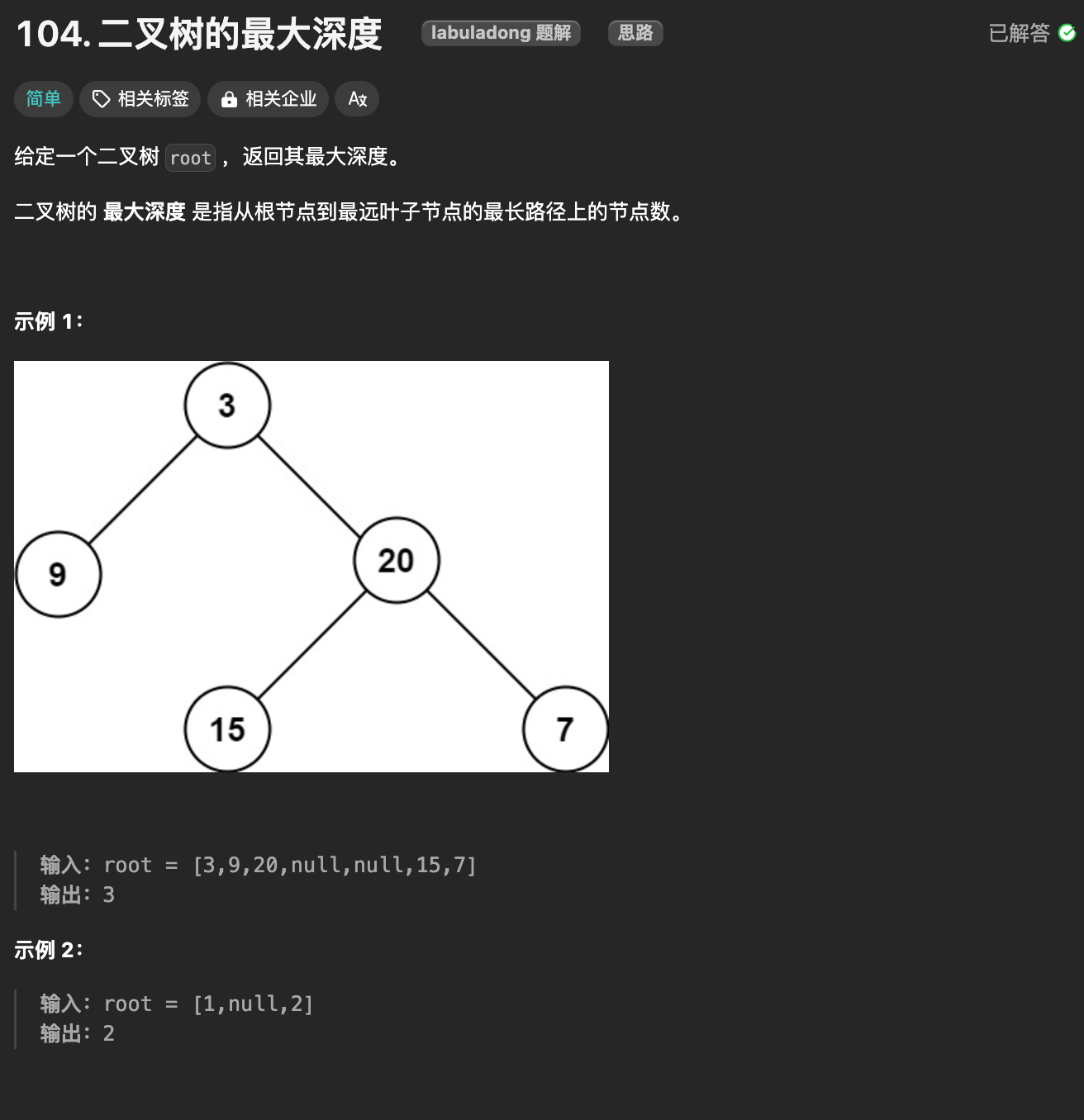
https://leetcode.cn/problems/maximum-depth-of-binary-tree/
3.2. 思路 1:遍历一遍二叉树的思路
遍历一遍二叉树- 用一个
外部变量 res记录每个节点所在的深度 - 变量
depth记录当前递归到的节点深度
- 用一个
- 最后,取
depth和res的最大值就可以得到最大深度,代码如下:
var maxDepth = function(root) {
let res = 0;
// depth 记录当前递归到的节点深度
let depth = 0;
function traverse(root) {
if(root === null) return;
depth++;
// 到达叶子节点
if(root.left === null && root.right === null){
res = Math.max(depth, res);
}
traverse(root.left);
traverse(root.right);
depth--;
}
traverse(root);
return res;
};
[!warning] 注意:函数命名和框架
traverse,这种规范的好处是直接套用就行,主要精力放在具体逻辑上就好,架子的东西都是个人习惯,但要统一,不然给自己添加成本
3.2.1. 复杂度分析
- 时间复杂度:O(n)
- 其中 n 是二叉树中的节点数。
- 这个算法会遍历二叉树的每个节点一次,因此时间复杂度是 O(n)。
- 空间复杂度:O(h)
- 其中 h 是二叉树的高度。
- 空间复杂度主要来自于递归调用栈的深度。
- 在最坏情况下(树完全不平衡,呈现为一条链),树的高度可能达到 n,此时空间复杂度为
O(n)。 - 在最好情况下(完全平衡二叉树),树的高度为 log(n),空间复杂度为
O(log n)。 - 因此,空间复杂度可以表示为 O(h),其中 h 是树的高度。
3.3. 思路 2:分解问题的思路
- 即通过
子树的最大深度推导出原树的深度 - 所以必然主要逻辑都在
后序位置,因为后序位置能够得到子树的深度。
var maxDepth = function (root) {
// base case
if (root == null) {
return 0;
}
// 利用定义,计算左右子树的最大深度
var leftMax = maxDepth(root.left);
var rightMax = maxDepth(root.right);
// 整棵树的最大深度等于左右子树的最大深度取最大值,
// 然后再加上根节点自己
var res = Math.max(leftMax, rightMax) + 1;
return res;
};
3.3.1. 复杂度分析
- 时间复杂度:O(n)
- 其中 n 是二叉树中的节点数。
- 这个算法会访问二叉树的每个节点一次,对每个节点进行常数时间的操作。
- 因此,总的时间复杂度是 O(n)。
- 空间复杂度:O(h)
- 其中 h 是二叉树的高度。
- 空间复杂度主要来自于递归调用栈的深度。
- 在最坏情况下(树完全不平衡,呈现为一条链),树的高度可能达到 n,此时空间复杂度为 O(n)。
- 在最好情况下(完全平衡二叉树),树的高度为 log(n),空间复杂度为 O(log n)。
- 因此,空间复杂度可以表示为 O(h),其中 h 是树的高度。