深入理解归并排序
#算法/排序
所有递归的算法,本质上都是在遍历一棵(递归)树,然后在节点(前中后序位置)上执行代码,你要写递归算法,本质上就是要告诉每个节点需要做什么。
目录
如何理解归归排序是二叉树的后序遍历
- 首先,一句话描述 归并排序?
- 先把
左半边数组排好序,再把右半边数组排好序,最后merge两个有序数组。
- 先把
下图是,遍历通过二叉树遍历思路,即非线性的方式,二叉树的前序遍历,来遍历数组,然后再离开节点的时候,做merge操作,如下图:
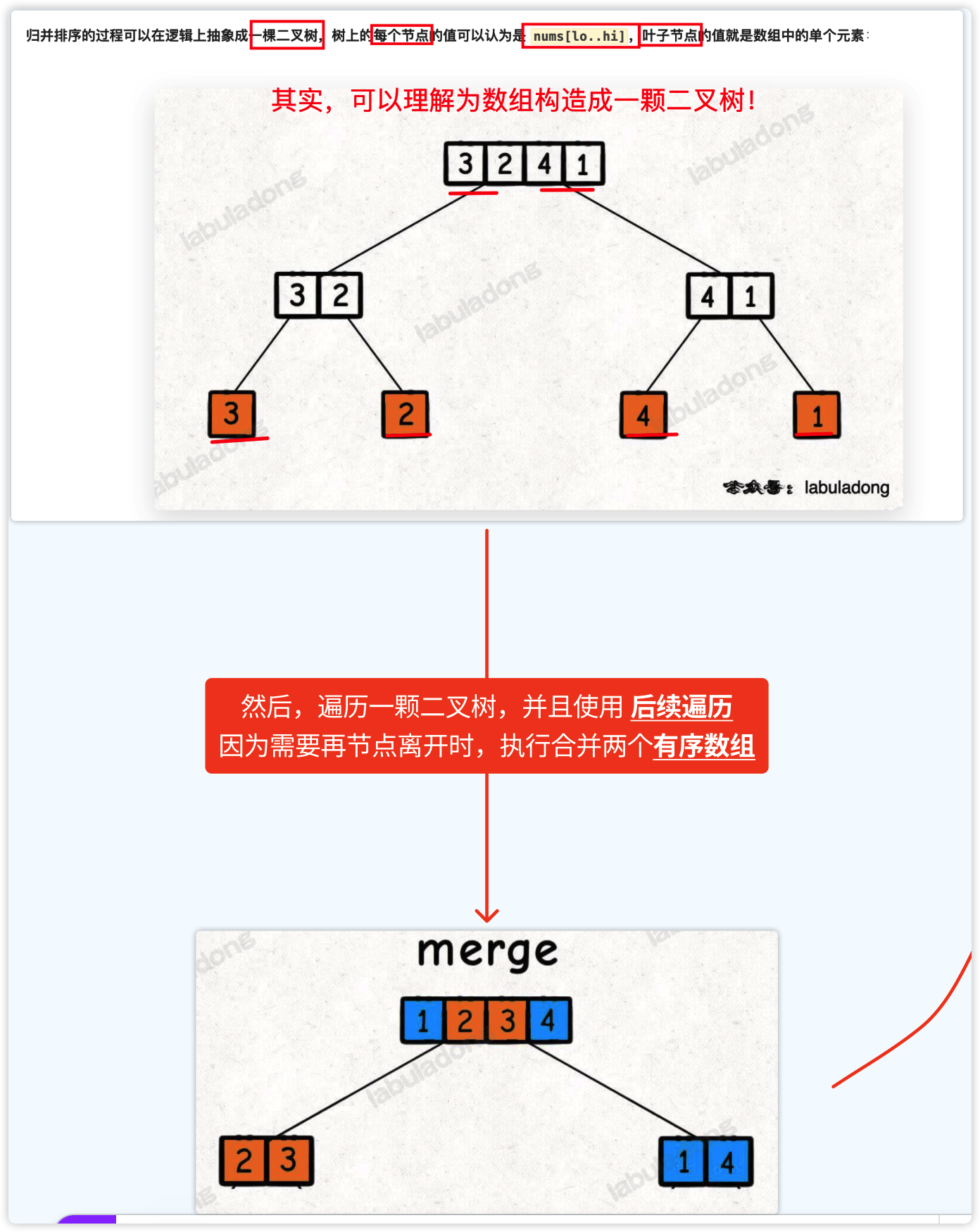
下面是 merge 的动图:
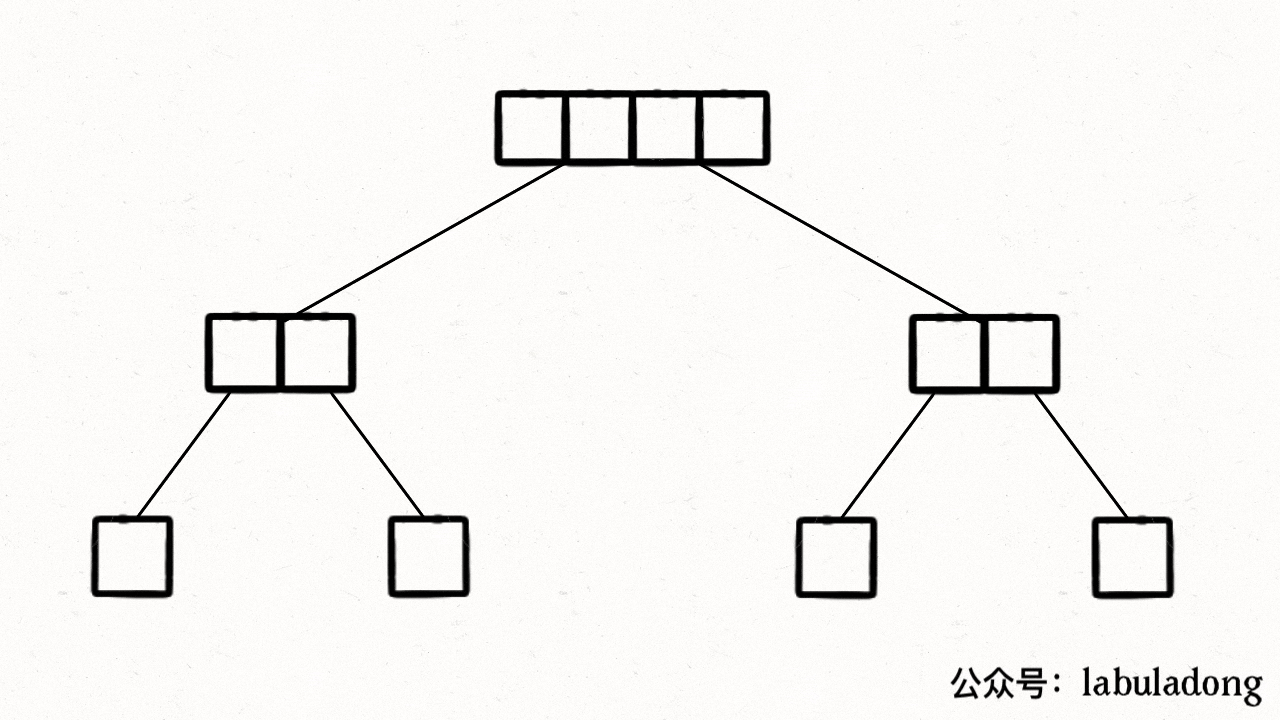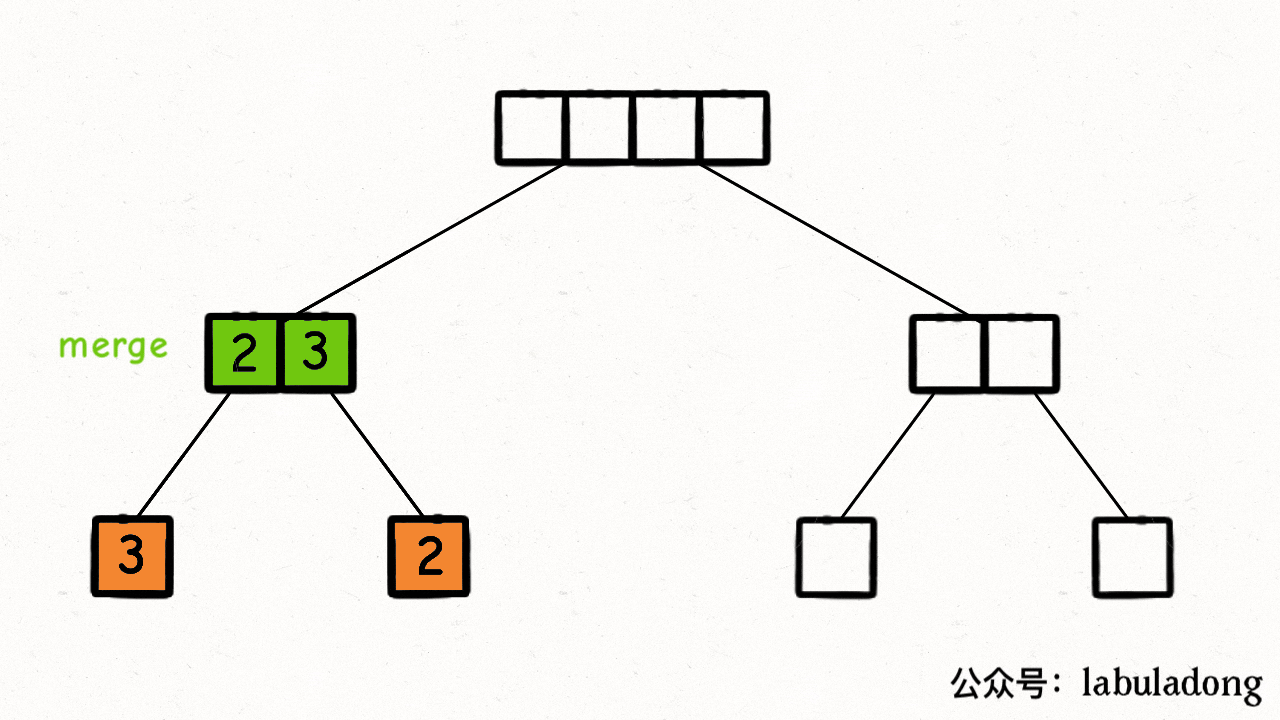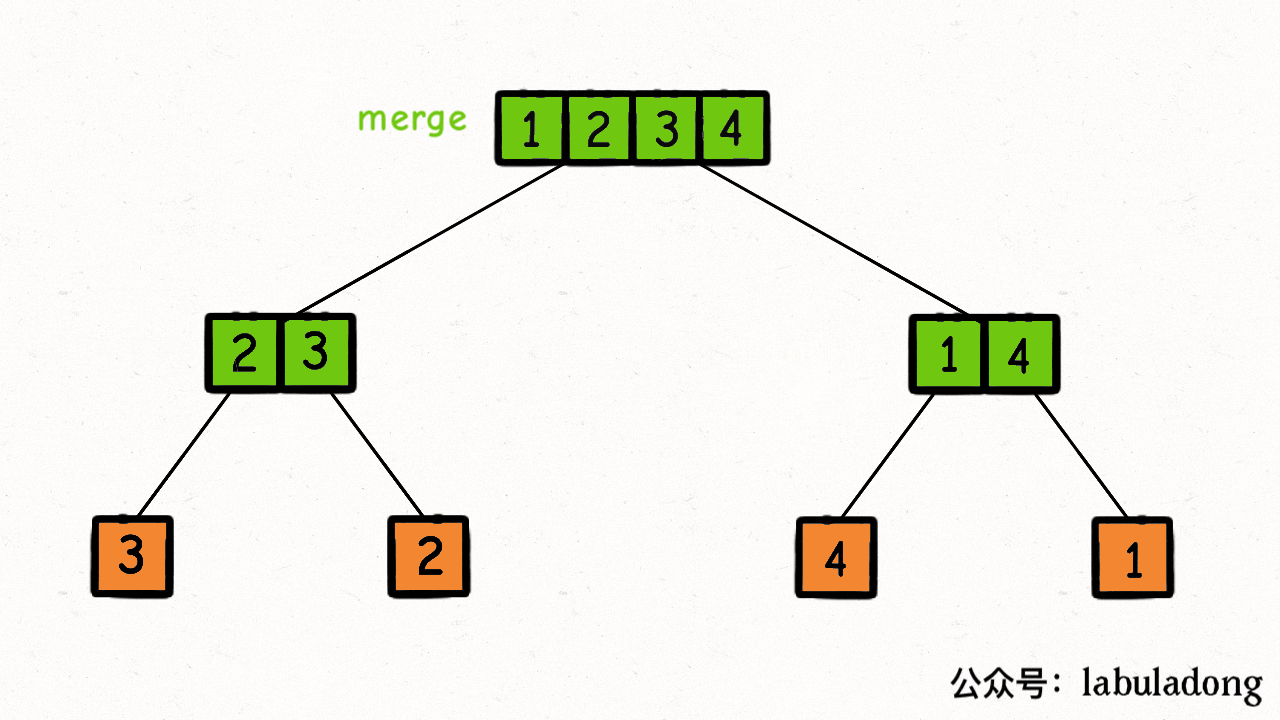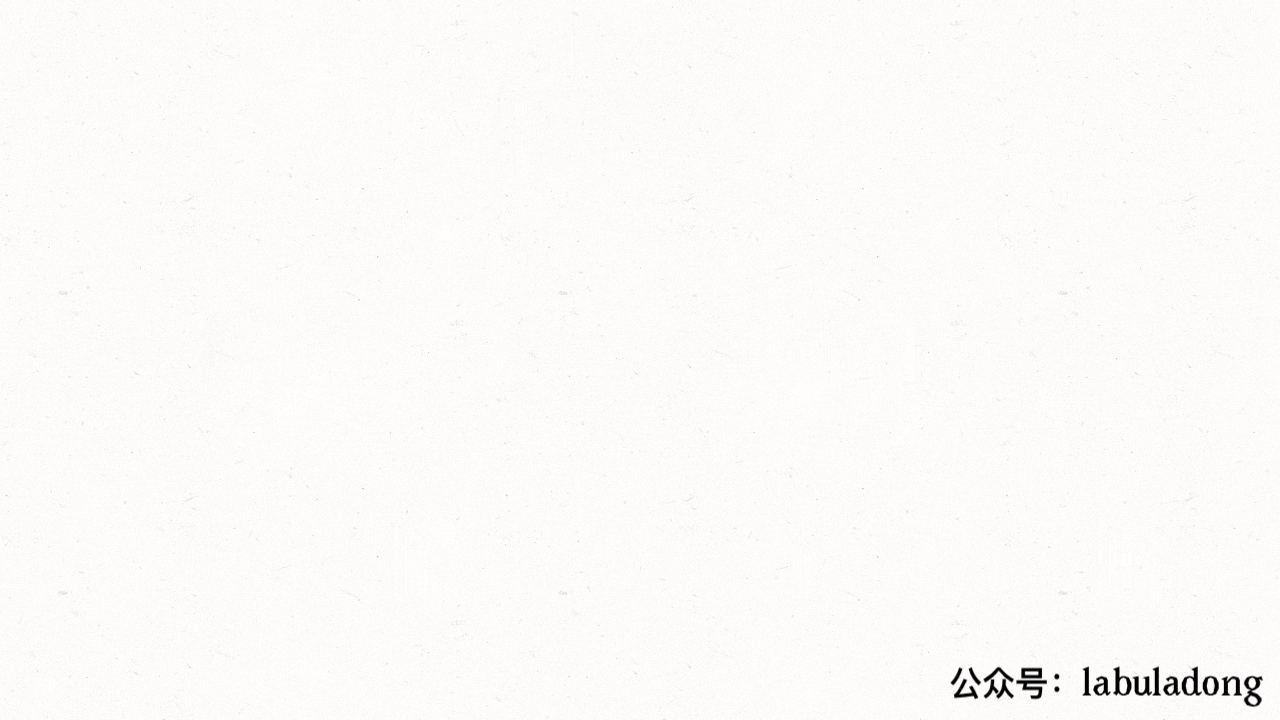
完全流程:先拆解,拆到叶子节点,然后再merge ,如下图:
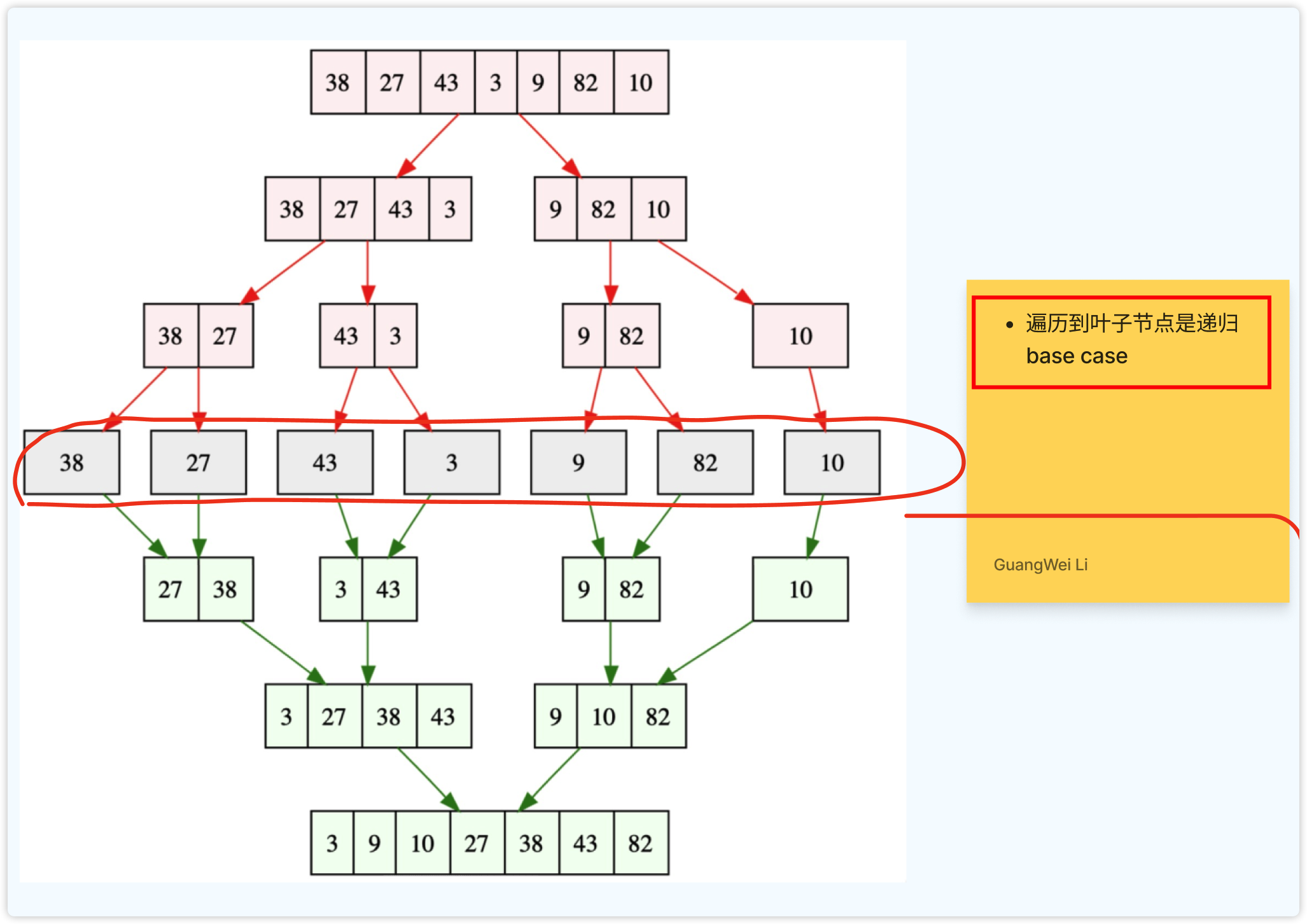
代码部分
测试用例:看 力扣(LeetCode)
/**
* https://leetcode.cn/problems/sort-an-array/
* */
function sort(nums, left, right) {
if (left === right) {
return;
}
const mid = Math.floor((left + right) / 2);
// 利用定义,排序 nums[left..mid]
sort(nums, left, mid);
// 利用定义,排序 nums[mid+1..right]
sort(nums, mid + 1, right);
// ::::后序位置::::
/*************************************************
* ::::即,此时两部分子数组已经被排好序
* :::: 合并两个有序数组,使 nums[left..right] 有序
************************************************/
merge(nums, left, mid, right);
}
// 使用 【数组双指针技巧】,合并两个有序数组
function merge(nums, left, mid, right) {
// copy 到 temp 数组
// ::::notice 不是 temp=[...nums]
const temp = []
for (let i = left; i <= right; i++) {
temp[i] = nums[i];
}
//// ::::使用 【数组双指针技巧】,合并两个有序数组
let i = left, j = mid + 1;
for (let p = left; p <= right; p++) {
// 左半边数组已全部被合并
if (i === mid + 1) { // :::: notice i === mid + 1
nums[p] = temp[j++];
// 右半边数组已全部被合并
} else if (j === right + 1) {
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
};
const arr = [5, 12, 13, 14, 4, 3, 15, 16, 2, 1, 2, 0, 2, 3, 9, 10, 11, 9, 17, 18, 19, 20, 21, 22];
sort(arr, 0, arr.length - 1);
console.log(arr);
- 都是
原地排序 - 注意,
sort和merge函数的入参分别是什么?
真正理解上面代码的双指针技巧吗?
对于 merge 的双指针,不一定真的的理解,下面梳理下:
以下图为例:
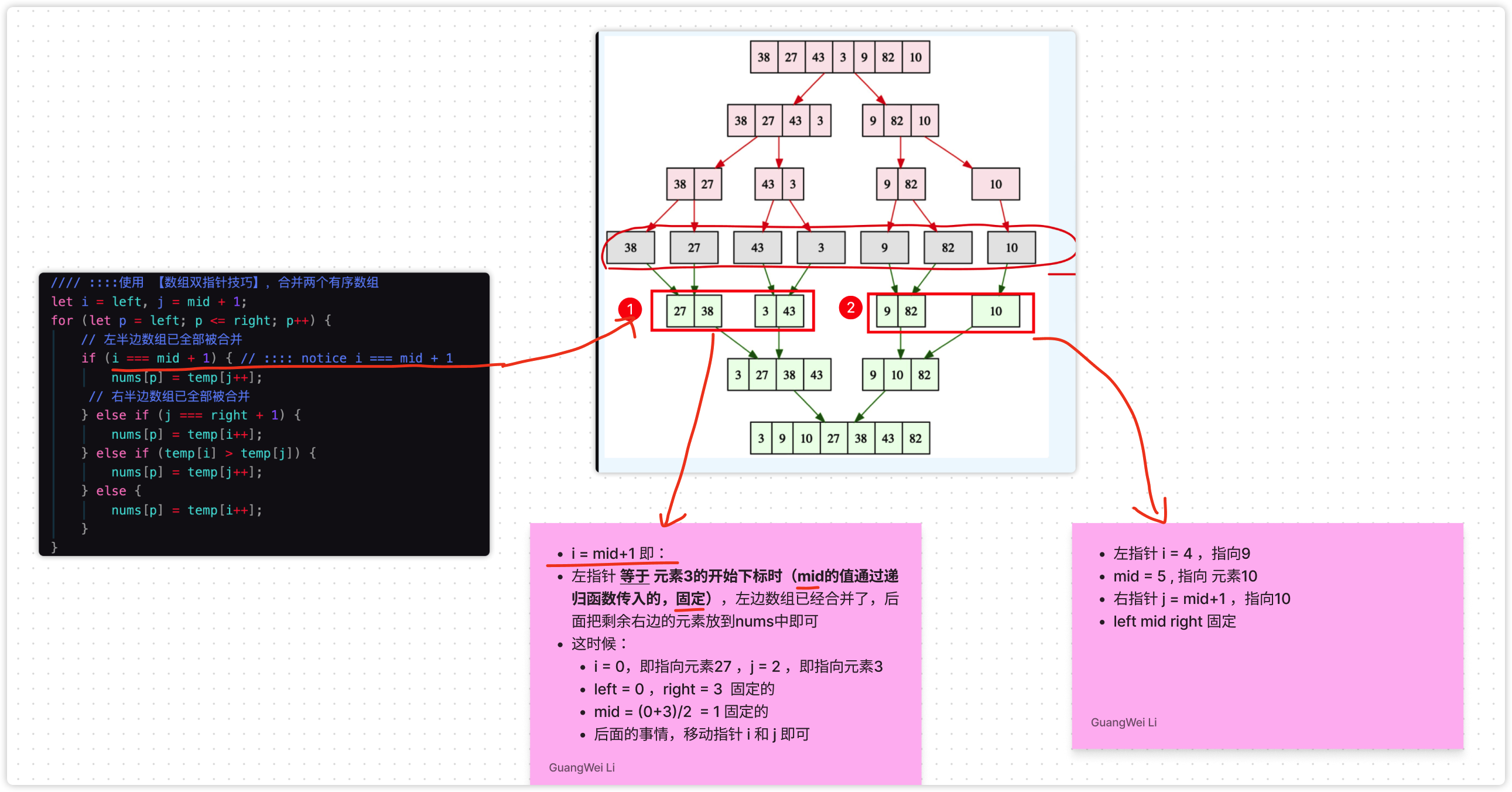
总之:
- 都是原地直接修改
nums - left , right , mid 都是递归函数传入的,固定的
双指针根据left和mid来初始化左指针i根据mid来判断 边界条件j右指针根据right来判断判断边界条件
[!info] 对于
递归的理解,还是一样,记住模板搞就是了,小脑袋瓜子,能递归几次?
另外一种解法:使用 js 的语法特性
const mergeSort = arr => {
// 采用自上而下的递归方法
const len = arr.length;
// 递归条件
if (len < 2) {
return arr;
}
let middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle); // 拆分为两个子数组
const leftArr = mergeSort(left);
const rightArr = mergeSort(right);
// ::::后序位置
return merge(leftArr, rightArr);
};
// 合并两个已经排好序的数组,无论left或者right里有多少元素
const merge = (left, right) => {
const result = [];
// :::: left和right都有元素,这判断大小后,取最小的放入结果集,注意使用shift了的副作用
while (left.length && right.length) {
//// :::: 注意: 判断的条件是小于或等于,如果只是小于,那么排序将不稳定.
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
// 走到这里,说明left和right其中一个为空,另一个不为空,遍历剩下的元素,放入结果集
// :::: 每次都取最小的放入结果集,注意使用shift了的副作用
while (left.length) result.push(left.shift());
while (right.length) result.push(right.shift());
return result;
};
const array = [5, 4, 3, 2, 1, 32, 2, 1, 0];
console.log('mergeSort ', mergeSort(array));
[!bug] 当初面试,就写不出来,不知道是
shift,还是left,right这几个变傻分不清了
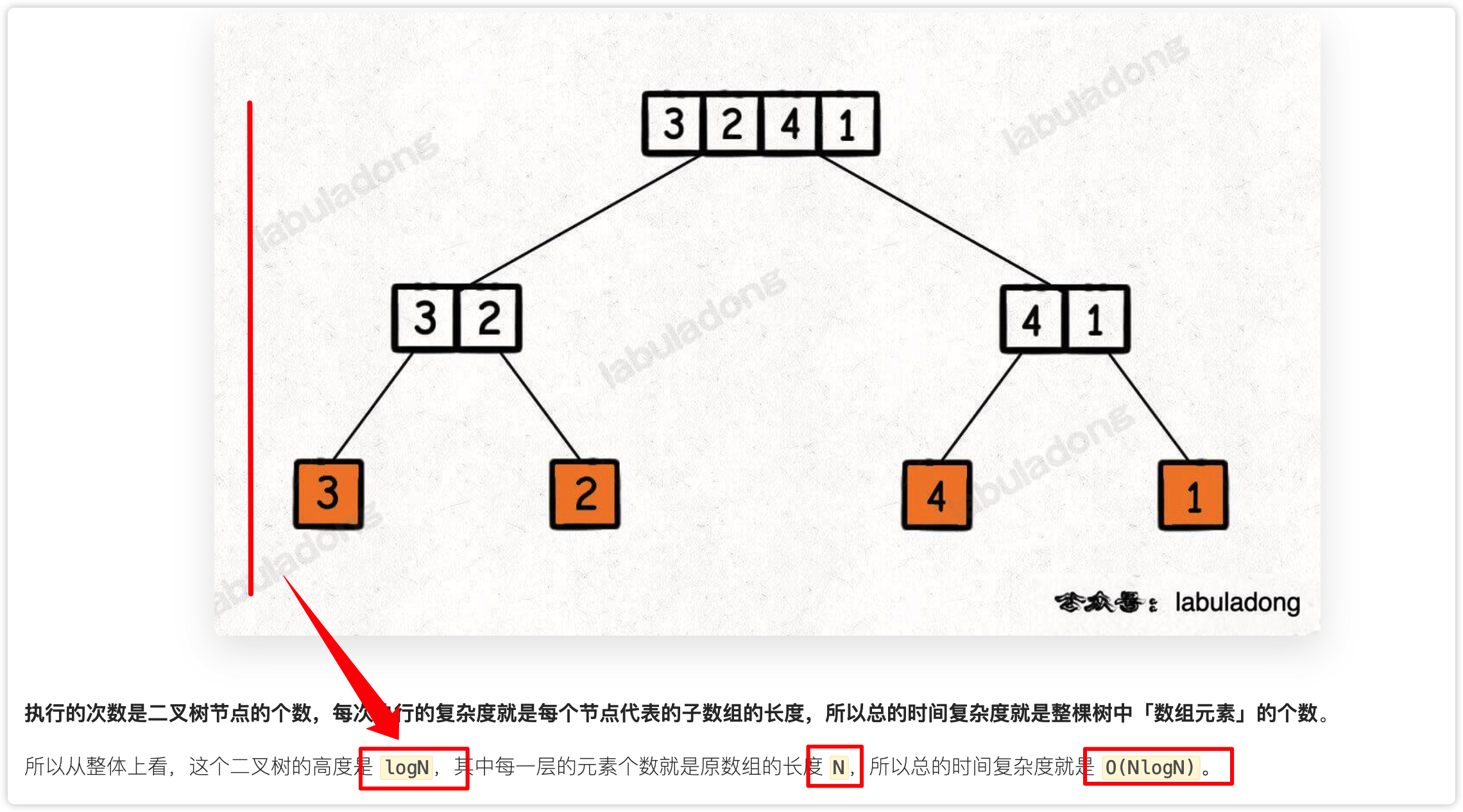
下面,分析一下复杂度