常见的随机算法
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 398. Random Pick Index | 398. 随机数索引 | 🟠 |
| 384. Shuffle an Array | 384. 打乱数组 | 🟠 |
| 382. Linked List Random Node | 382. 链表随机节点 | 🟠 |
目录
第 384 题「打乱数组」
var Solution = function (nums) {
this.nums = nums;
this.copy = [...nums];
};
Solution.prototype.reset = function () {
return this.nums;
};
// 洗牌算法
Solution.prototype.shuffle = function () {
const n = this.nums.length;
for (let i = 0; i < n; i++) {
// 生成一个 [i, n-1] 区间内的随机数
const r = i + Math.floor(Math.random() * (n - i));
// 交换 copy[i] 和 copy[r]
[this.copy[i], this.copy[r]] = [this.copy[r], this.copy[i]];
}
return this.copy;
};
水塘抽样算法(Reservoir Sampling)
水塘抽样算法是一个随机采样算法,它可以从一个包含未知大小的数据流中随机选择 k 个样本。这个算法的特点是:
- 只需要遍历一次数据
- 对内存的使用是恒定的
- 保证每个元素被选中的概率相等
水塘抽样算法:从数据流中随机选择一个元素(k=1):
// 从数据流中随机选择一个元素
function reservoirSample(stream) {
let result = null; // 存储最终选中的元素
let count = 0; // 记录当前处理的元素个数
for (const item of stream) {
count++;
// 以 1/count 的概率选择当前元素
if (Math.random() < 1/count) {
result = item;
}
}
return result;
}
// 示例使用
const stream = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
console.log(reservoirSample(stream));
水塘抽样算法:从数据流中随机选择 k 个元素:
// 从数据流中随机选择k个元素
function reservoirSampleK(stream, k) {
const reservoir = []; // 存储最终选中的k个元素
let count = 0; // 记录当前处理的元素个数
// 处理前k个元素
for (const item of stream) {
count++;
if (count <= k) {
// 前k个元素直接放入水塘中
reservoir.push(item);
} else {
// 对于第k个之后的元素
// 以 k/count 的概率选择当前元素替换水塘中的随机一个
const j = Math.floor(Math.random() * count);
if (j < k) {
reservoir[j] = item;
}
}
}
return reservoir;
}
// 示例使用
const stream = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const k = 3;
console.log(reservoirSampleK(stream, k));
算法原理解释:
- 对于 k=1 的情况:
- 当处理第 i 个元素时,以 1/i 的概率选择该元素
- 这样保证了每个元素最终被选中的概率都是相等的
- 对于选择 k 个元素的情况:
- 前 k 个元素直接放入结果集合中
- 对于第 i 个元素(i > k):
- 以 k/i 的概率决定是否选择当前元素
- 如果选择当前元素,则随机替换结果集合中的一个元素
数学证明:
- 对于任意位置的元素,最终被选中的概率都是 k/n(n为总元素个数)
- 这保证了算法的公平性,每个元素都有相同的概率被选中
使用场景:
- 从大数据流中随机抽样
- 在内存受限的情况下需要随机选择元素
- 在线算法中需要保持随机样本
- 大规模日志分析中的采样
注意事项:
- 算法的空间复杂度是 O(k)
- 时间复杂度是 O(n),其中 n 是数据流的长度
- 算法只需要遍历一次数据
- 生成的随机数要足够随机,以保证采样的公平性
这个算法在处理大规模数据流时特别有用,因为它不需要预先知道数据的总量,而且内存使用是固定的。
第 382 题「链表随机节点」
/**
* @param {ListNode} head
*/
var Solution = function (head) {
this.head = head;
this.r = Math.random;
};
/**
* @return {number}
*/
Solution.prototype.getRandom = function () {
let i = 0,
res = 0;
let p = this.head;
// while 循环遍历链表
while (p !== null) {
i++;
// 生成一个 [0, i) 之间的整数
// 这个整数等于 0 的概率就是 1/i
if (Math.floor(this.r() * i) === 0) {
res = p.val;
}
p = p.next;
}
return res;
};
398. 随机数索引
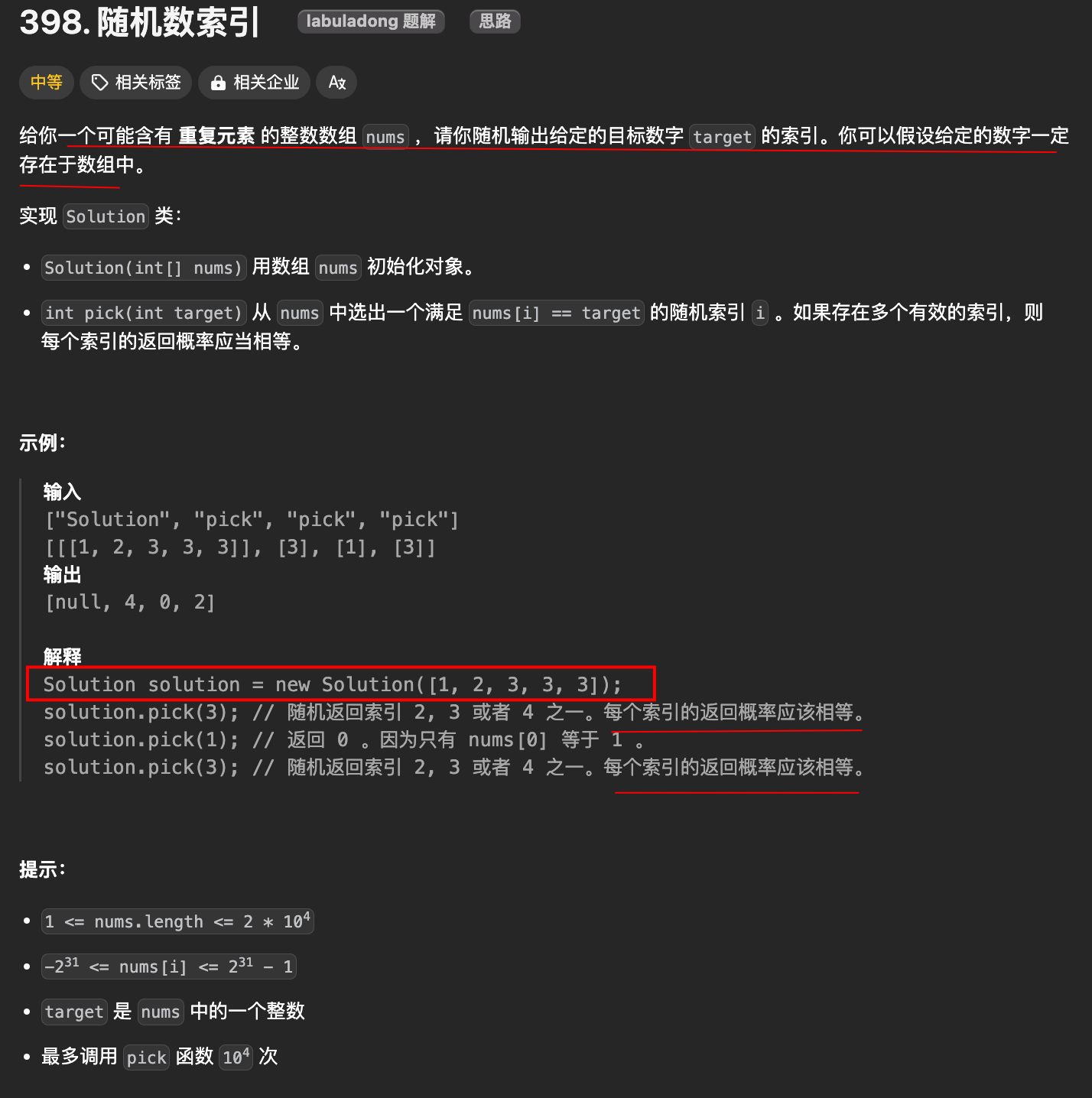
var Solution = function (nums) {
this.nums = nums;
this.rand = Math.random;
};
Solution.prototype.pick = function (target) {
let count = 0,
res = -1;
for (let i = 0; i < this.nums.length; i++) {
if (this.nums[i] !== target) {
continue;
}
count++;
if (Math.floor(this.rand() * count) === 0) {
res = i;
}
}
return res;
};