回溯算法解题框架

#算法/回溯 #算法/DFS

1. 回溯算法框架

站在回溯树的一个节点上，你只需要==思考 3 点==

路径：也就是已经做出的选择。
选择列表：也就是你当前可以做的选择。
结束条件：也就是到达决策树底层，无法再做选择的条件。

const result = [];

function backtrack('路径', '选择列表') {
    if ('满足结束条件') {
        result.add('路径');
        return;
    }
    for (let '选择' of '选择列表') {
        // 做选择;
        backtrack('路径', '选择列表');
        // 撤销选择;
    }
}

其核心就是 for 循环里面的递归

在递归调用之前 「做选择」
在递归调用之后 「撤销选择」

关于这个框架的原理解释？见下面全排列的分析，你就明白了

为什么里面有个 for 循环？

因为回溯算法本质是一个==多叉树的遍历==

4. N 皇后

https://leetcode.cn/problems/n-queens/

比如， N = 4，那么你就要在 4x4 的棋盘上放置 4 个皇后，返回以下结果（用 . 代表空棋盘，Q 代表皇后），如下图：

|584

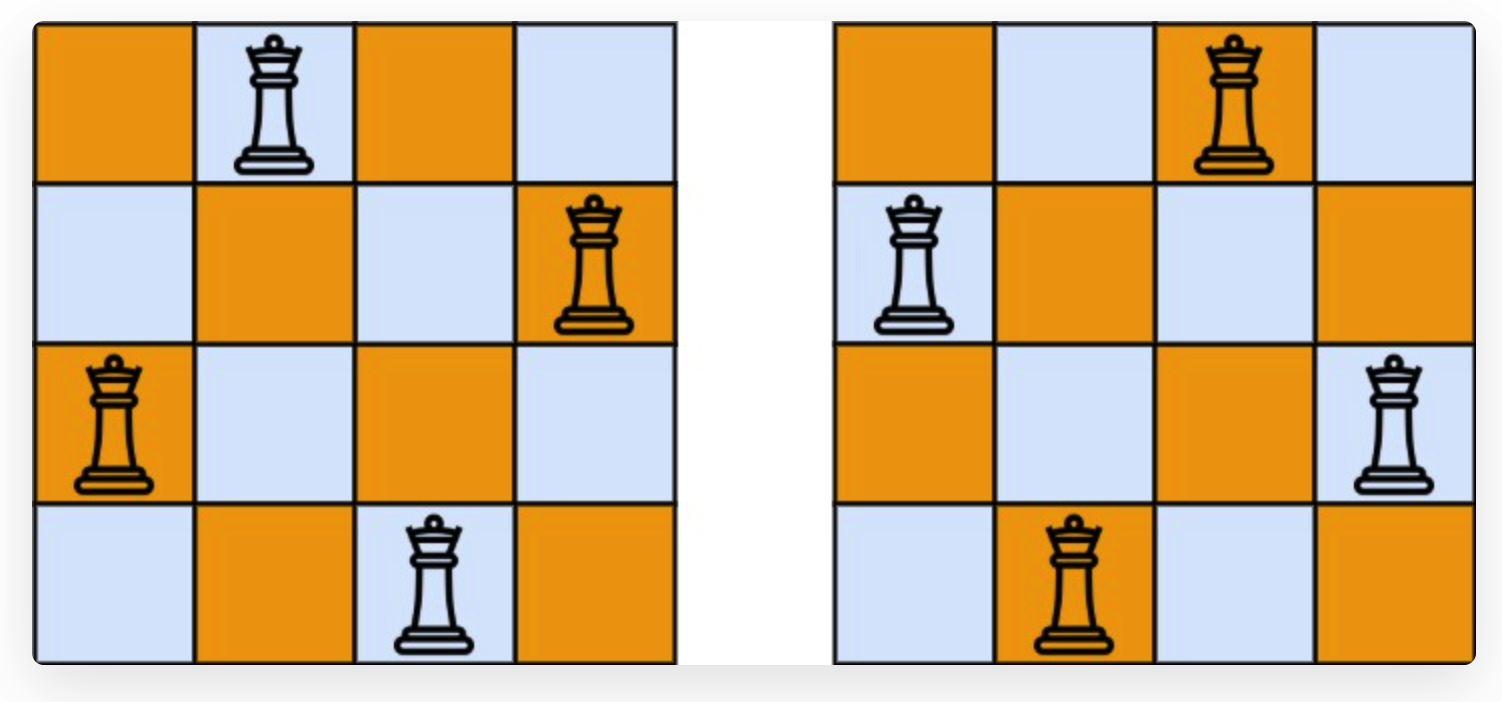
皇后可以攻击同一行、同一列、左上左下 右上右下 四个方向的任意单位。

4.1. 附：`初始化`一个 `m*n` 的`二维数组` 最简便的方式

|664

/**
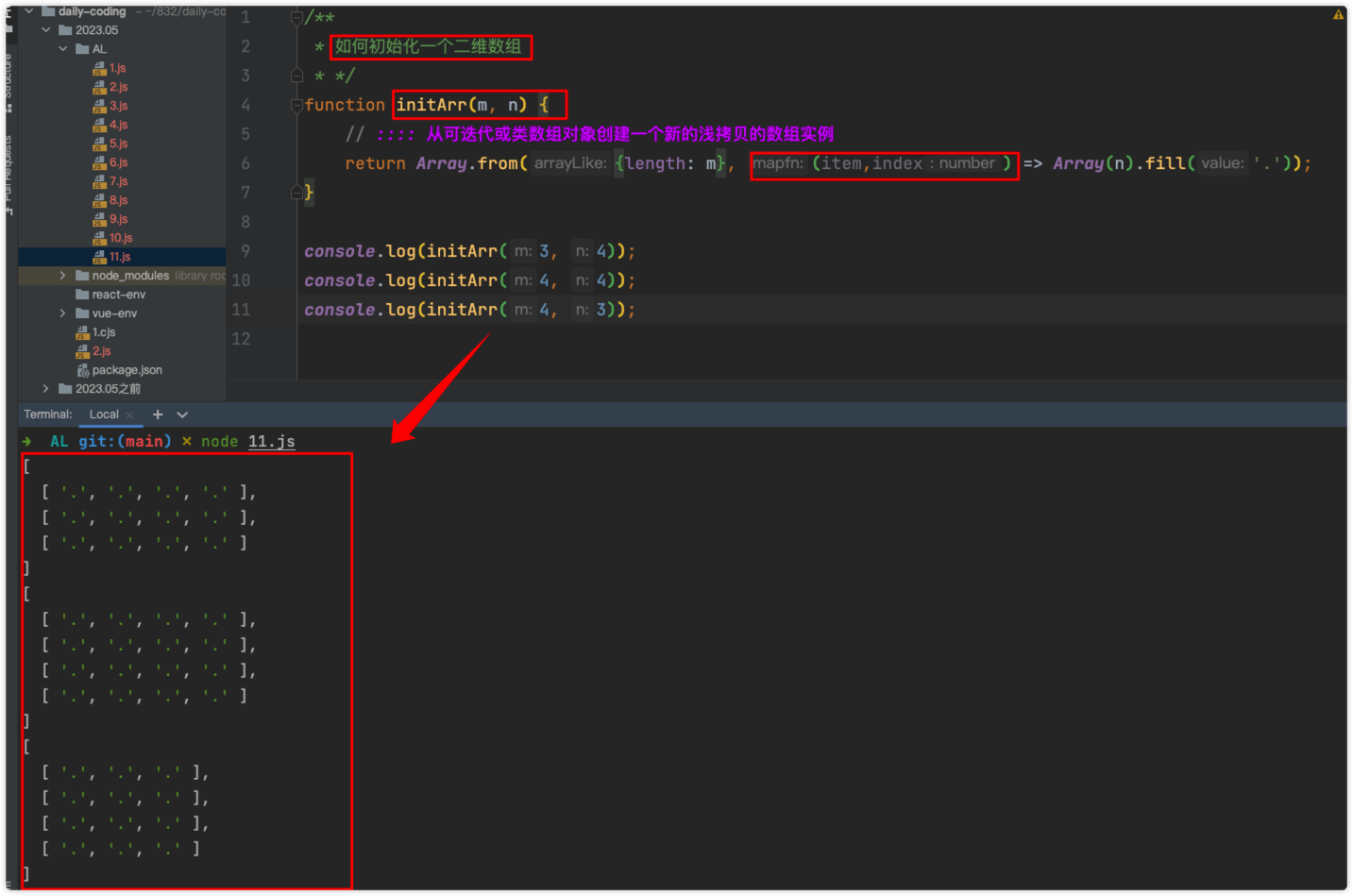
 * 如何初始化一个二维数组
 * */
function initArr(m, n) {
    // :::: 从可迭代或类数组对象创建一个新的浅拷贝的数组实例
    return Array.from({length: m}, (item,index) => Array(n).fill('.'));
}

console.log(initArr(3, 4));
console.log(initArr(4, 4));
console.log(initArr(4, 3));

4.2. 代码实现

/**
 * https://leetcode.cn/problems/n-queens/
 * */
let solveNQueens = function (n) {
    let res = [];
    let board = Array.from({length: n}, () => Array(n).fill('.'));
    /**
     * @param board 棋盘二维数组
     * @param row 当前第几行
     * */
    let backtrack = function (board, row) {
        // :::: 满足结束条件, 即已经放置了 n 个皇后
        if (row === board.length) {
            // 看题设，需要输出这样的格式
            const item = board.map((row) => row.join(''));
            res.push(item);
            return;
        }
        // :::: 从选择列表中选择,这里的选择列表是【二维数组的第 row 行】
        // 换句话来说，从 第row行  中去选择 某一列
        let currentRow = board[row].length;
        for (let col = 0; col < currentRow; col++) {
            if (!isValid(board, row, col)) {
                continue;
            }
            // :::: 做选择
            board[row][col] = 'Q';
            backtrack(board, row + 1);
            // :::: 撤销选择
            board[row][col] = '.';
        }
    }; 
    let isValid = function (board, row, col) {
        let totalRow = board.length;
        // 检查 【当前列】 是否有皇后互相冲突
        // 所以 列数col不变，行数变化
        for (let i = 0; i < row; i++) {
            if (board[i][col] === 'Q') {
                return false;
            }
        }
        // 检查【右上方】是否有皇后互相冲突
        for (let i = row - 1, j = col + 1; i >= 0 && j < totalRow; i--, j++) {
            if (board[i][j] === 'Q') {
                return false;
            }
        }
        // 检查【左上方】 是否有皇后互相冲突
        for (let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (board[i][j] === 'Q') {
                return false;
            }
        }
        return true;
    };
    backtrack(board, 0);
    return res;
};

关于，isValid 的逻辑，分析可见 fj

https://www.figma.com/file/hT9k2YbVvV1UIITtUmbJ0C/2023.05.LOG?type=whiteboard&node-id=161-198&t=Cw0r27yobQ8yinDi-4

|984

回溯算法中，如果只需要一个结果即可，如上题中，只需要一个符合规范的 N 皇后布局，外部变量标识是否找到，找到直接 return 即可，如下代码：

// 函数找到一个答案后就返回 true
var found = false;

function backtrack(board, row) {
    // 已经找到一个答案了，不用再找了
    if (found) {
        return;
    }
    // 触发结束条件
    if (row === board.length) {
        res.push(board);
        // 找到了第一个答案
        found = true;
        return;
    }
    ...
}

5. N 皇后 II

https://leetcode.cn/problems/n-queens-ii/

把上题改成返回个数而已，其他都不需要变，把 res = 0 即可，因为 res=[] 肯定更占内存。代码如下：


let totalNQueens = function (n) {
    let res = 0;
    let board = Array.from({length: n}, () => Array(n).fill('.'));
    /**
     * @param board 棋盘二维数组
     * @param row 当前第几行
     * */
    let backtrack = function (board, row) {
        // :::: 满足结束条件, 即已经放置了 n 个皇后
        if (row === board.length) {
            res++;
            return;
        }
        // :::: 从选择列表中选择,这里的选择列表是【二维数组的第 row 行】
        // 换句话来说，从 第row行  中去选择 某一列
        let currentRowLen = board[row].length;
        for (let col = 0; col < currentRowLen; col++) {
            if (!isValid(board, row, col)) {
                continue;
            }
            // :::: 做选择
            board[row][col] = 'Q';
            backtrack(board, row + 1);
            // :::: 撤销选择
            board[row][col] = '.';
        }
    };

    let isValid = function (board, row, col) {
        let totalRow = board.length;
        // 检查 【上方】 是否有皇后互相冲突
        // 所以 列数col不变，行数变化
        for (let i = 0; i < row; i++) {
            if (board[i][col] === 'Q') {
                return false;
            }
        }
        // 检查【右上方】是否有皇后互相冲突
        for (let i = row - 1, j = col + 1; i >= 0 && j < totalRow; i--, j++) {
            if (board[i][j] === 'Q') {
                return false;
            }
        }
        // 检查【左上方】 是否有皇后互相冲突
        for (let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (board[i][j] === 'Q') {
                return false;
            }
        }
        return true;
    };
    backtrack(board, 0);
    return res;
};

5.1. 复杂度分析

当 N = 8 时，就是八皇后问题，数学大佬高斯穷尽一生都没有数清楚八皇后问题到底有几种可能的放置方法，但是我们的算法只需要一秒就可以算出来所有可能的结果。 ==所以，计算机真的很强大==

N 行棋盘中，第一行有 N 个位置可能可以放皇后，第二行有 N - 1 个位置，第三行有 N - 2 个位置，以此类推，再叠加每次放皇后之前 isValid 函数所需的 O(N) 复杂度，所以总的时间复杂度上界是 O(N! * N) 。

liguwe's site