单调列队算法

#leetcode #2024/08/11 #算法/单调列队 #算法/数据结构算法

第 239 题「滑动窗口最大值」

目录

• 1. 定义
• 2. 用途
• 3. 单调递减队列的实现
  • 3.1. push(item) 的逻辑
  • 3.2. pop(item) 的逻辑
• 4. LeetCode：滑动窗口最大值
  • 4.1. 题目
  • 4.2. 使用单调列队来解
  • 4.3. 复杂度分析

1. 定义

队列中的元素全都是单调递增（或递减）的

2. 用途

• 它可以快速确定滑动窗口中的最大或最小值
  • 单调队列结合滑动窗口方法可以在O(1)时间内计算当前窗口中的最大值或最小值
  • 同时保持队列先进先出的特性

3. 单调递减队列的实现

先看看 普通的队列的标准 API

// 普通的队列的标准 API
class Queue {
  // enqueue 操作，在队尾加入元素 n
  push(n) {}

  // dequeue 操作，删除队头元素
  pop() {}
}

单调递减队列的标准 API

// 单调递减队列的标准 API
class MonotonicQueue {
  // 在队尾添加元素 n
  push(n) {}

  // 返回队头元素
  max() {}

  // 删除队头元素
  pop() {}
}

下面是具体实现

// 单调递增队列的标准 API
class MonotonicQueue {
  constructor() {
    // 维护其中的元素自尾部到头部单调递增
    this.maxq = [];
  }

  // 在队尾添加元素 item
  // 在尾部添加一个元素 item，维护 maxq 的单调性质
  // 将前面小于自己的元素都删
  push(item) {
    // 将前面小于自己的元素都删除
    while (this.maxq.length > 0 && this.maxq[this.maxq.length - 1] < item) {
      // 删除数组的最后一个元素
      this.maxq.pop();
    }
    this.maxq.push(item);
  }

  // 返回队头元素, 即 maxq 队首元素
  // 队头的元素肯定是最大的
  max() {
    return this.maxq[0];
  }

  // 删除队头元素,
  pop(item) {
    // 如果要删除的元素是队头元素，就删除
    // 否则不做任何操作
    // 想删除的队头元素 item 可能已经被「压扁」了
    if (this.maxq[0] === item) {
      // 删除数组的第一个元素
      this.maxq.shift();
    }
  }
}

3.1. push(item) 的逻辑

关于 push(item) 的逻辑，可以参考下图

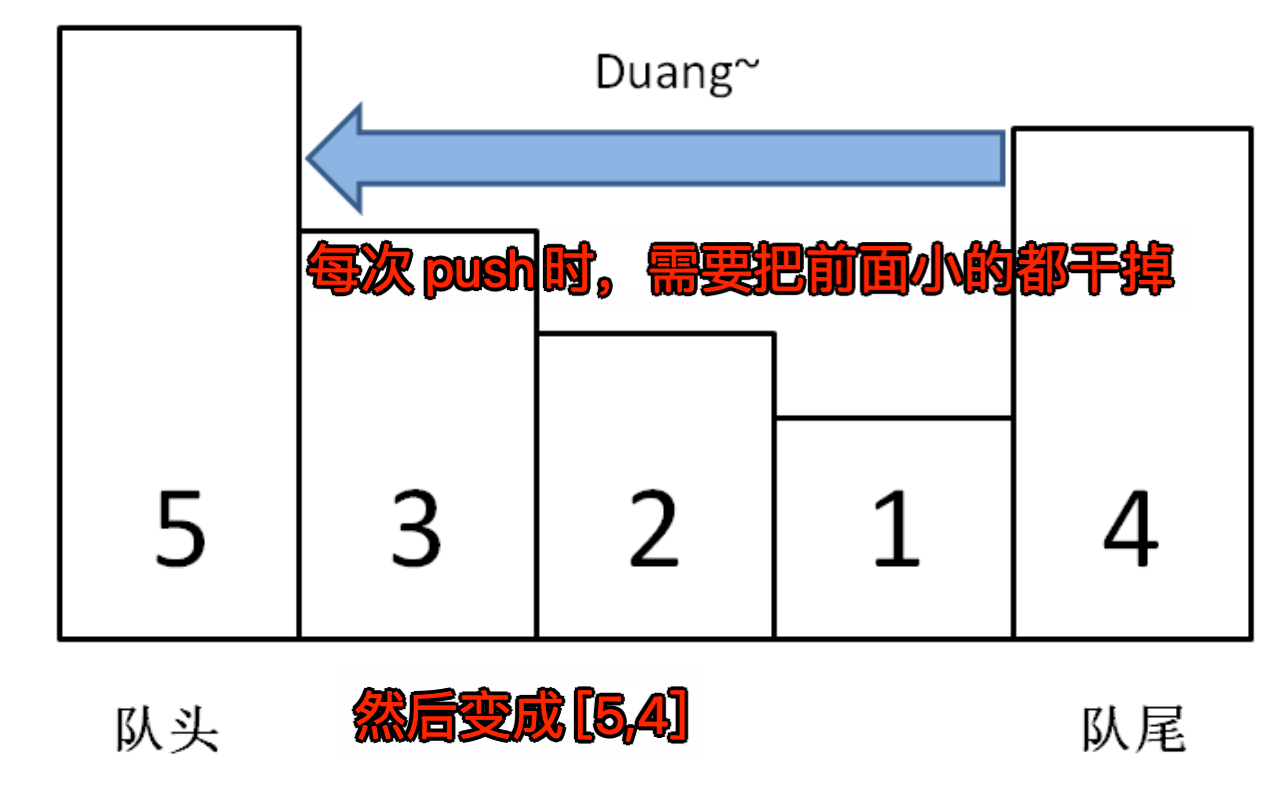
[!danger] 会有疑问❓，都 pop 删除了，那岂不是队列里没值了，不是因为每次都会 push ，长度都会+1 ，即使把前面的元素都干掉了，长度还是持续增加

3.2. pop(item) 的逻辑

删除队首，需要传一个参数，如果它是队首元素才需要删除

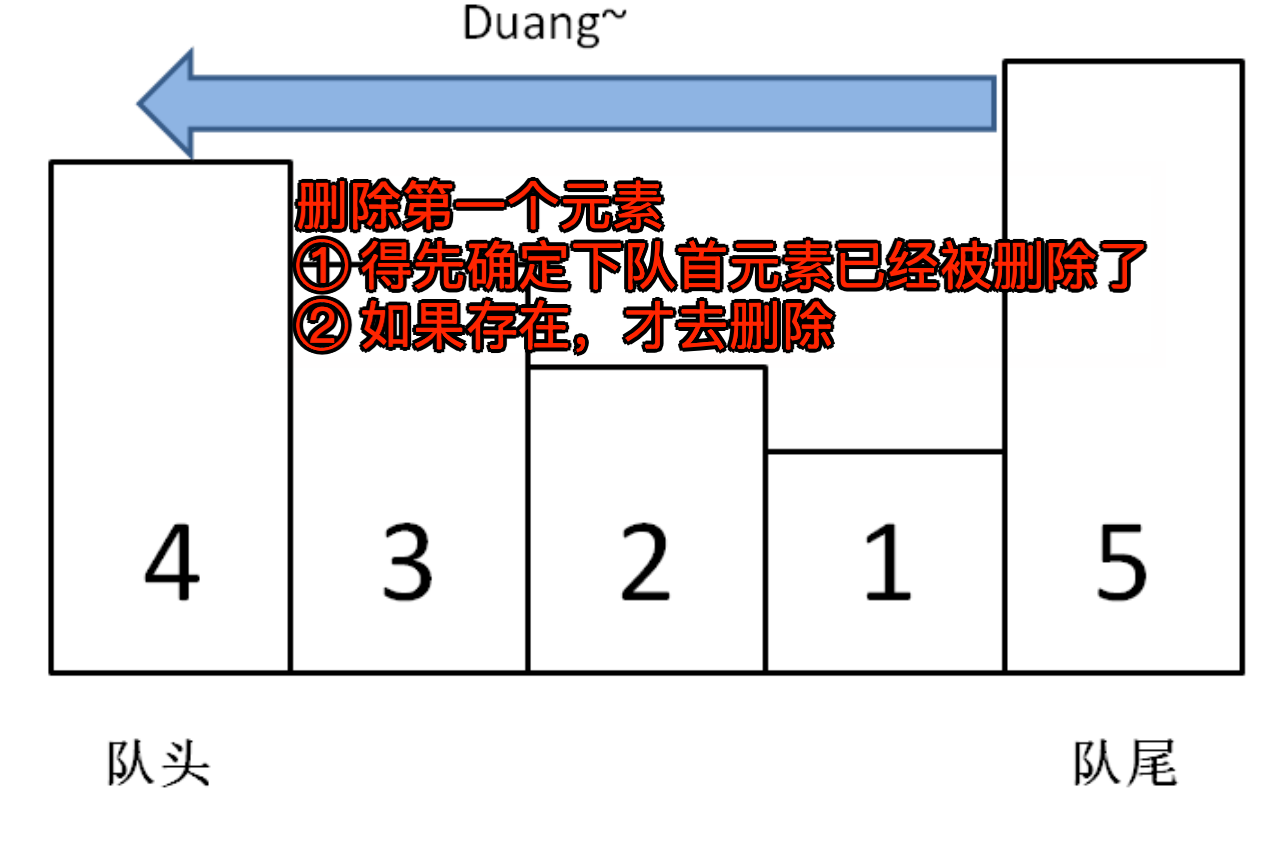
4. LeetCode：滑动窗口最大值

第 239 题「滑动窗口最大值」

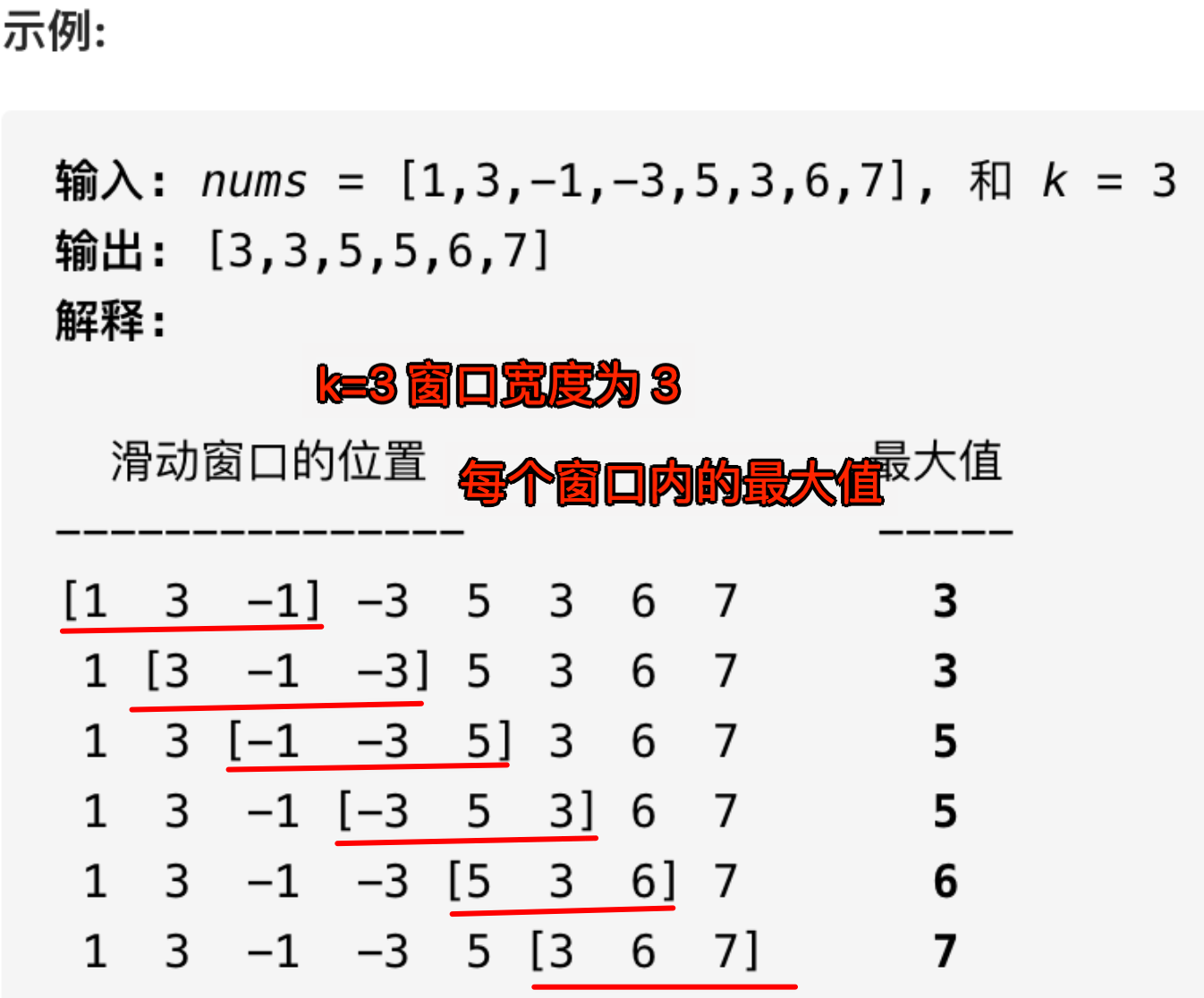
4.1. 题目

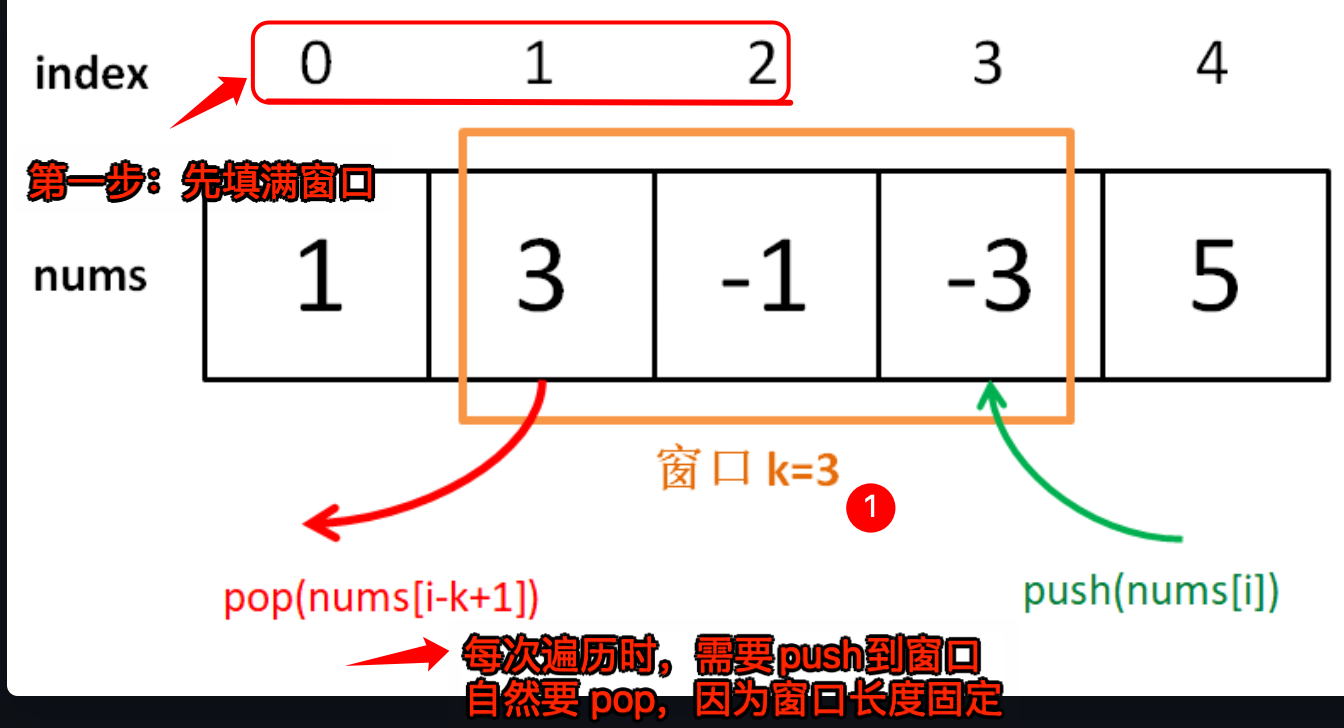
4.2. 使用单调列队来解

• 解题思路
  • ① 初始化一个单调队列，用于维护移动窗口
  • ② 遍历数组
    • 先填满窗口，每次 push 时，window 都会维护一个单调递减队列
    • 填满了，每次先后移动一次，需要做以下事情
      • window.push(item)
      • res.push(window.max())
      • 删除对首元素，因为需要保证 window 的长度为 k

// 单调递增队列的标准 API
class MonotonicQueue {
  constructor() {
    // 维护其中的元素自尾部到头部单调递增
    this.maxq = [];
  }
  // 在队尾添加元素 item
  // 在尾部添加一个元素 item，维护 maxq 的单调性质
  // 将前面小于自己的元素都删
  push(item) {
    // 将前面小于自己的元素都删除
    while (this.maxq.length > 0 && this.maxq[this.maxq.length - 1] < item) {
      this.maxq.pop();
    }
    this.maxq.push(item);
  }
  // 返回队头元素, 即 maxq 队首元素
  // 队头的元素肯定是最大的
  max() {
    return this.maxq[0];
  }

  // 删除队头元素
  pop(item) {
    // 如果要删除的元素是队头元素，就删除
    // 否则不做任何操作
    // 想删除的队头元素 item 可能已经被「压扁」了
    if (this.maxq[0] === item) {
      this.maxq.shift();
    }
  }
}

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var maxSlidingWindow = function (nums, k) {
  // ① 初始化一个单调队列，用来维护窗口的最大值
  // 变量 window 是一个 MonotonicQueue 类型的实例
  let window = new MonotonicQueue();

  let res = [];

  // 遍历 nums
  for (let i = 0; i < nums.length; i++) {
    // ①  如果 i < k - 1，先填满窗口的前 k - 1
    if (i < k - 1) {
      window.push(nums[i]);
    } else {
      // ②  窗口向前滑动，加入最后一个元素
      // 每次 push时，window 都会维护一个单调递减队列
      window.push(nums[i]);
      // 记录当前窗口的最大值
      res.push(window.max());
      // 窗口向前滑动，删除第一个元素
      window.pop(nums[i - k + 1]);
    }
  }

  return res;
};

4.3. 复杂度分析

• 时间复杂度：O(n)
  • 主循环遍历整个数组 nums，这需要 O(n) 时间，其中 n 是数组的长度。
    • 在循环中，我们执行以下操作：
      • push(): 虽然这个操作包含一个while循环，看起来可能是O(n)
        • 但是每个元素最多被 push 和 pop 一次。
        • 所以整个数组，push操 作的均摊时间复杂度是O(1)
      • max(): 这是一个O(1)操作，因为它只是返回队列的第一个元素。
      • pop(): 这也是一个O(1)操作，因为它只是检查并可能删除队列的第一个元素。
  • 综上所述，尽管有嵌套的循环，但是由于每个元素最多被处理两次（一次入队，一次出队），所以总的时间复杂度是O(n)
• 空间复杂度：O(k)
  • MonotonicQueue 中的 maxq 数组在最坏情况下可能会存储 k 个元素，其中 k 是滑动窗口的大小。
  • 结果数组 res 的大小为 n - k + 1，但这是必要的输出空间，通常不计入空间复杂度。