丑数问题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 313. Super Ugly Number | 313. 超级丑数 | 🟠 |
| 264. Ugly Number II | 264. 丑数 II | 🟠 |
| 1201. Ugly Number III | 1201. 丑数 III | 🟠 |
| 263. Ugly Number | 263. 丑数 | 🟢 |
目录
1. 第 263 题「丑数」
所谓「丑数」,就是只包含质因数 2、3 和 5 的正整数
var isUgly = function (n) {
if (n <= 0) return false;
// 如果 n 是丑数,分解因子应该只有 2, 3, 5
while (n % 2 == 0) n /= 2;
while (n % 3 == 0) n /= 3;
while (n % 5 == 0) n /= 5;
// 如果能够成功分解,说明是丑数
return n == 1;
};
2. 第 264 题「丑数 II」
题目:给你输入一个 n,让你计算第 n 个丑数是多少
思路:
- 抽象出三条有序的丑数链表,合并这三条有序链表得到的结果就是丑数序列,其中第
n个丑数就是题目想要的答案 - 我们用
p2, p3, p5分别代表三条丑数链表上的指针,用product2, product3, product5代表丑数链表上节点的值,用ugly数组记录有序链表合并之后的结果。
var nthUglyNumber = function (n) {
// 可以理解为三个指向有序链表头结点的指针
let p2 = 1,
p3 = 1,
p5 = 1;
// 可以理解为三个有序链表的头节点的值
let product2 = 1,
product3 = 1,
product5 = 1;
// 可以理解为最终合并的有序链表(结果链表)
let ugly = new Array(n + 1);
// 可以理解为结果链表上的指针
let p = 1;
// 开始合并三个有序链表,找到第 n 个丑数时结束
while (p <= n) {
// 取三个链表的最小结点
let min = Math.min(Math.min(product2, product3), product5);
// 将最小节点接到结果链表上
ugly[p] = min;
p++;
// 前进对应有序链表上的指针
if (min == product2) {
product2 = 2 * ugly[p2];
p2++;
}
if (min == product3) {
product3 = 3 * ugly[p3];
p3++;
}
if (min == product5) {
product5 = 5 * ugly[p5];
p5++;
}
}
// 返回第 n 个丑数
return ugly[n];
};
3. 第 313 题「超级丑数」
输入一个质数列表 primes 和一个正整数 n,请你计算第 n 个「超级丑数」
所谓超级丑数是一个所有质因数都出现在 primes 中的正整数
3.1. 示例
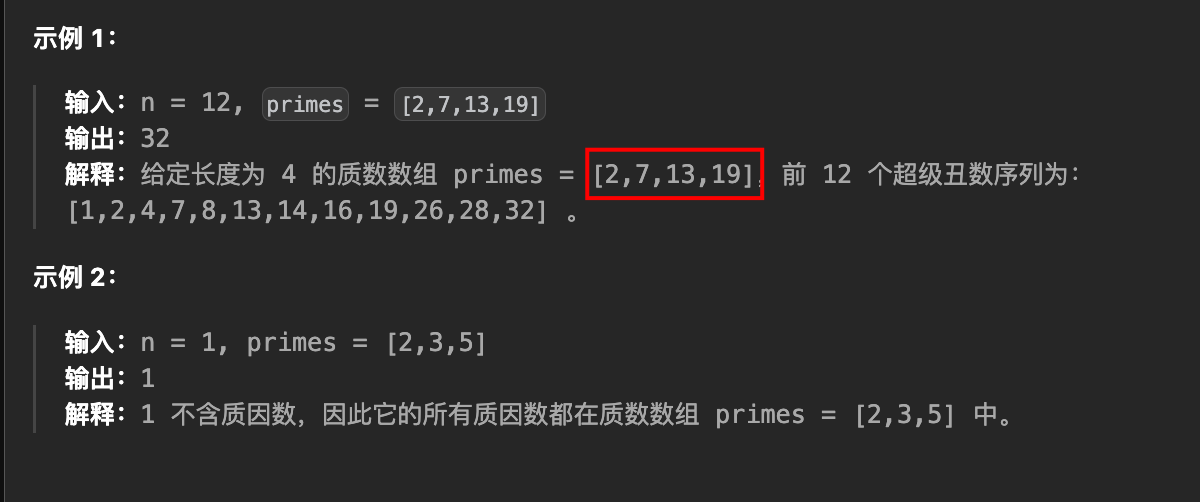
如果让 primes = [2, 3, 5] 就是上道题:第 263 题「丑数」,但我们不能用 min 函数计算最小头结点了,而是要用优先级队列来计算最小头结点,同时依然要维护链表指针、指针所指节点的值,我们可以用一个三元组 来保存这些信息
看代码
var nthSuperUglyNumber = function (n, primes) {
// 优先队列中装三元组:{ product, prime, pi}
// 其中 product 代表链表节点的值,prime 是计算下一个节点所需的质数因子, pi 代表链表上的指针
let pq = new MinPriorityQueue({ priority: (pair) => pair[0] });
for (let prime of primes) {
pq.enqueue([1, prime, 1]);
}
// 可以理解为最终合并的有序链表(结果链表)
let ugly = new Array(n + 1);
// 可以理解为结果链表上的指针
let p = 1;
while (p <= n) {
// 取三个链表的最小结点
let pair = pq.dequeue().element;
let product = pair[0];
let prime = pair[1];
let index = pair[2];
// 避免结果链表出现重复元素
if (product != ugly[p - 1]) {
// 接到结果链表上
ugly[p] = product;
p++;
}
// 生成下一个节点加入优先级队列
pq.enqueue([ugly[index] * prime, prime, index + 1]);
}
return ugly[n];
};
4. 第 1201 题「丑数 III」
4.1. 题目
给你四个整数:n, a, b, c,请你设计一个算法来找出第 n 个丑数。其中丑数是可以被 a 或 b 或 c 整除的正整数。
这道题和之前题目的不同之处在于它改变了丑数的定义,只要一个正整数 x 存在 a, b, c 中的任何一个因子,那么 x 就是丑数。
比如输入 n = 7, a = 3, b = 4, c = 5,那么算法输出 10,因为符合条件的丑数序列为 3, 4, 5, 6, 8, 9, 10, ...,其中第 7 个数字是 10。
有了之前几道题的铺垫,你肯定可以想到把 a, b, c 的倍数抽象成三条有序链表:
1*3 -> 2*3 -> 3*3 -> 4*3 -> 5*3 -> 6*3 -> 7*3 ->...
1*4 -> 2*4 -> 3*4 -> 4*4 -> 5*4 -> 6*4 -> 7*4 ->...
1*5 -> 2*5 -> 3*5 -> 4*5 -> 5*5 -> 6*5 -> 7*5 ->...
然后将这三条链表合并成一条有序链表并去除重复元素,这样合并后的链表元素就是丑数序列,我们从中找到第 n 个元素即可:
1*3 -> 1*4 -> 1*5 -> 2*3 -> 2*4 -> 3*3 -> 2*5 ->...
写出代码
4.2. 代码:超时
var nthUglyNumber = function (n, a, b, c) {
// 可以理解为三个有序链表的头结点的值
let productA = a,
productB = b,
productC = c;
// 可以理解为合并之后的有序链表上的指针
let p = 1;
let minProduct = -666;
// 开始合并三个有序链表,获取第 n 个节点的值
while (p <= n) {
// 取三个链表的最小结点
minProduct = Math.min(productA, productB, productC);
p++;
// 前进最小结点对应链表的指针
if (minProduct == productA) {
productA += a;
}
if (minProduct == productB) {
productB += b;
}
if (minProduct == productC) {
productC += c;
}
}
return minProduct;
};
注意题目给的数据范围非常大,a, b, c, n 的大小可以达到 10^9,所以即便上述算法的时间复杂度是 O(n),也是相对比较耗时的,应该有更好的思路能够进一步降低时间复杂度。
4.3. 解决思路
定义一个单调递增的函数 f:
f(num, a, b, c)计算[1..num]中,能够整除a或b或c的数字的个数- 显然函数
f的返回值是随着num的增加而增加的(单调递增)
- 显然函数
- 题目让我们求第
n个能够整除a或b或c的数字是什么,也就是说我们要找到一个最小的num,使得f(num, a, b, c) == n。
var nthUglyNumber = function (n, a, b, c) {
// 题目说本题结果在 [1, 2 * 10^9] 范围内,
// 所以就按照这个范围初始化两端都闭的搜索区间
let left = 1,
right = 2 * 10 ** 9;
// 搜索左侧边界的二分搜索
while (left <= right) {
let mid = left + Math.floor((right - left) / 2);
if (f(mid, a, b, c) < n) {
// [1..mid] 中符合条件的元素个数不足 n,所以目标在右半边
left = mid + 1;
} else {
// [1..mid] 中符合条件的元素个数大于 n,所以目标在左半边
right = mid - 1;
}
}
return left;
};
// 计算最大公因数(辗转相除/欧几里得算法)
var gcd = function (a, b) {
if (a < b) {
// 保证 a > b
return gcd(b, a);
}
if (b === 0) {
return a;
}
return gcd(b, a % b);
};
// 最小公倍数
var lcm = function (a, b) {
// 最小公倍数就是乘积除以最大公因数
return (a * b) / gcd(a, b);
};
// 计算 [1..num] 之间有多少个能够被 a 或 b 或 c 整除的数字
var f = function (num, a, b, c) {
let setA = Math.floor(num / a),
setB = Math.floor(num / b),
setC = Math.floor(num / c);
let setAB = Math.floor(num / lcm(a, b));
let setAC = Math.floor(num / lcm(a, c));
let setBC = Math.floor(num / lcm(b, c));
let setABC = Math.floor(num / lcm(lcm(a, b), c));
// 集合论定理:A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C
return setA + setB + setC - setAB - setAC - setBC + setABC;
};