计算机算法的框架思维

#算法 #算法框架

目录

1. 先分清两种算法

先分清，两种算法，他们是完全不同的思维

  • 计算机算法
    • 本质是 穷举 ，因为计算机就是快
    • 难点
      • 一些算法的难点是如何”无遗漏“的穷举所有可能
      • 一些算法的难点是如何”聪明“的穷举
  • 数学算法
    • 本质是 数学
    • 学数学的 后遗症 ， 别想着 能不能推导出一个什么数学公式

2. 如何”无遗漏“的穷举所有

如递归类问题，最典型的是动态规划问题，它的状态转移方程是最难写出来的

3. 技巧：如何”聪明“的穷举

至少 二分查找、快慢指针、左右指针、滑动窗口、前缀和数组、差分数组，这些你得知道

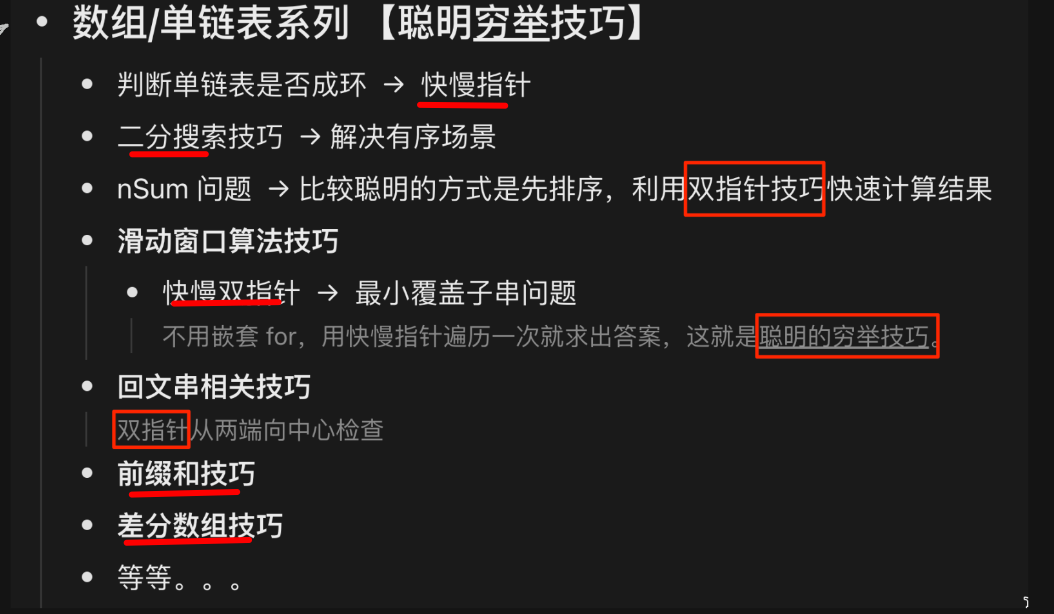
3.1. 数组链表技巧

  • 双指针技巧
    • 快慢指针技巧
    • 前后指针技巧
  • 二分搜索技巧
  • 前缀和技巧
  • 差分数组技巧

如下图：

|544

3.2. 二叉树技巧

3.2.1. 两种思路

  • 遍历的思路
  • 分解问题的思路

|584

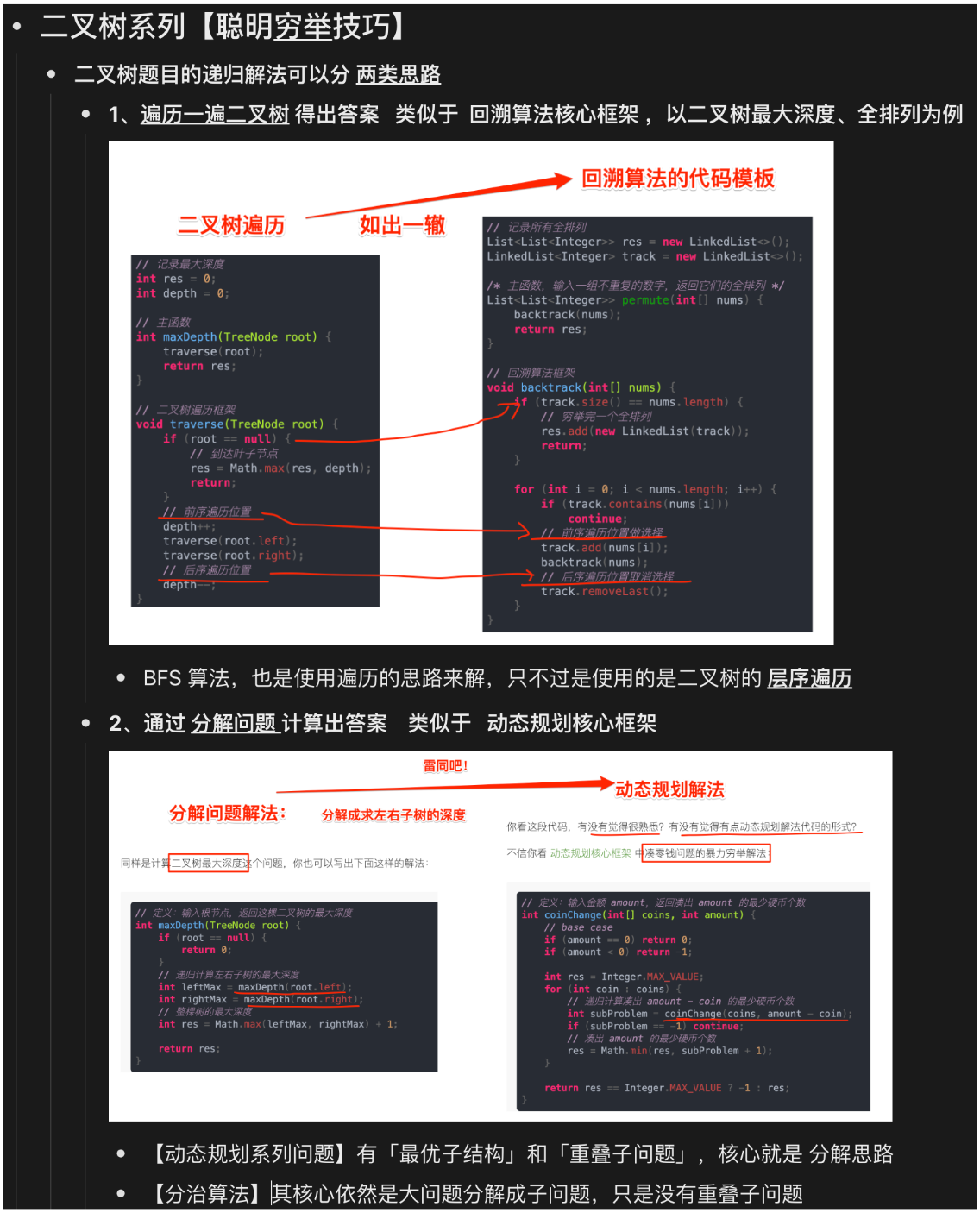
3.2.2. 前序遍历的 遍历思路 和 分解问题思路

|536

[!bug] 是的，避免死磕，难道用锯子去挖石头，因为技巧储备还不够，一切是徒劳，很多属于会者不难。

4. 算法与数据结构

  • 各种算法像是精美的拼图
  • 而数据结构是组成这些拼图的模块

4.1. 其实底层就两种存储方式：链表 + 数组

  • 链表（链式存储）
    • 栈、队列：可用 链表实现
    • 散列表： 可用链表：拉链法实现
    • 图：可使用 链表：邻接表实现
  • 树
    • 堆（完全二叉树）
      • 可使用数组实现吗
    • 非完全二叉树
      • 可使用链表实现
  • 数组（顺序存储）
    • 栈、队列：也可以数组实现
    • 散列表： 也可用数组：线性探测法实现
    • 图：可使用 数组：邻接矩阵 实现
    • 树
      • 堆（完全二叉树）
        • 可使用数组实现

[!info] 1、上面的对应关系，旨在说明 数据存储 底层就两种存储方式：数组 和 链表

2、数组和链表才是「结构基础」

4.2. 数据结构操作：其实就遍历 + 访问（增删改查） 两种

  • 两种基本操作
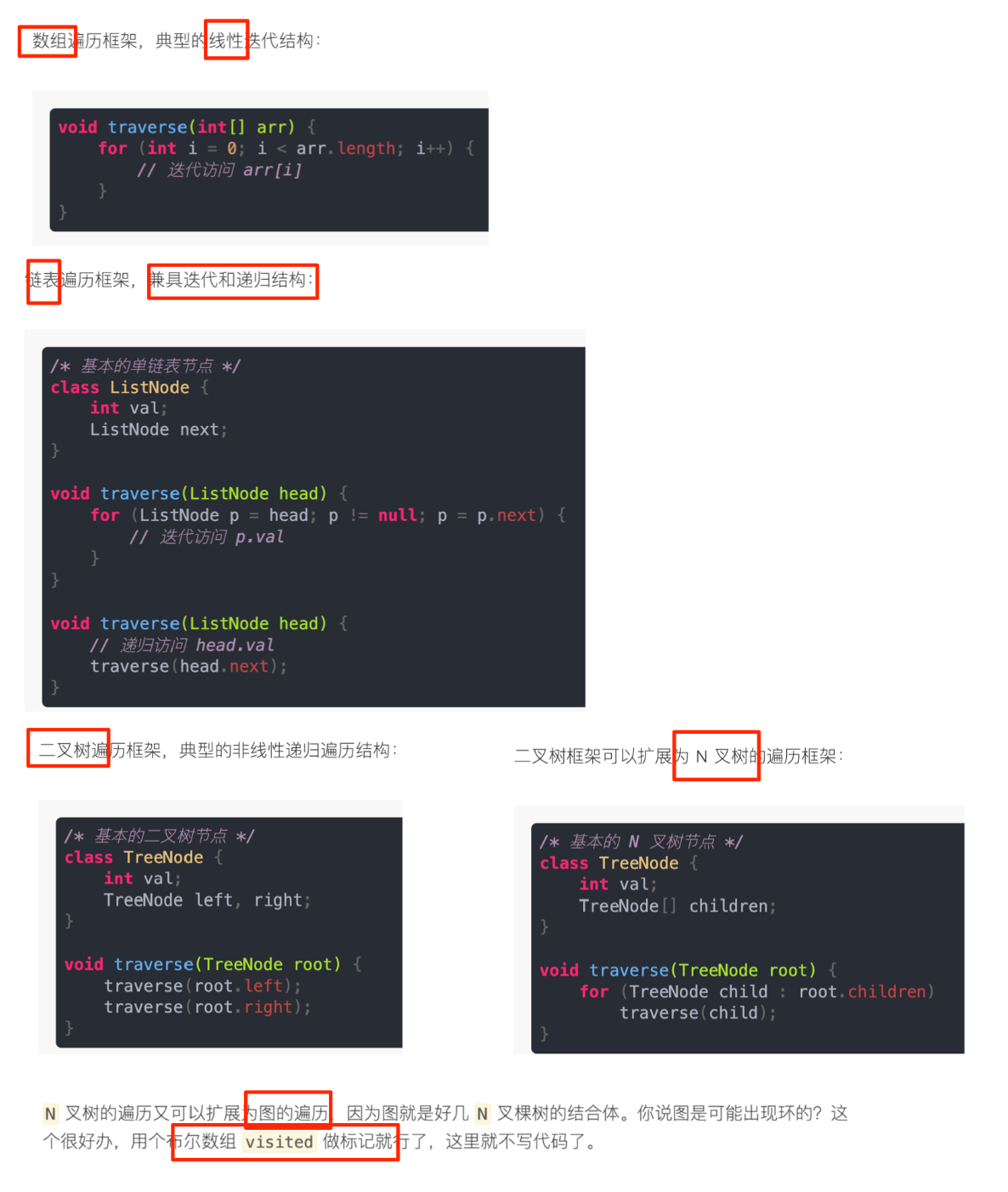
    • 遍历 ，遍历又分两种
      • 线性迭代遍历
      • 非线性递归遍历
    • 访问（增删查改）
      • 数据结构存在的使命，不就是 尽可能高效的增删查改

4.2.1. 所有的遍历框架

|616