二叉树的构造

目录

• 4. 通过后序和中序遍历结果构造二叉树
  • 4.1. 再看后序与中序
• 5. 通过后序和前序遍历结果构造二叉树
• 6. 最后

4. 通过后序和中序遍历结果构造二叉树

这是力扣第 106 题「 从后序和中序遍历序列构造二叉树」

4.1. 再看后序与中序

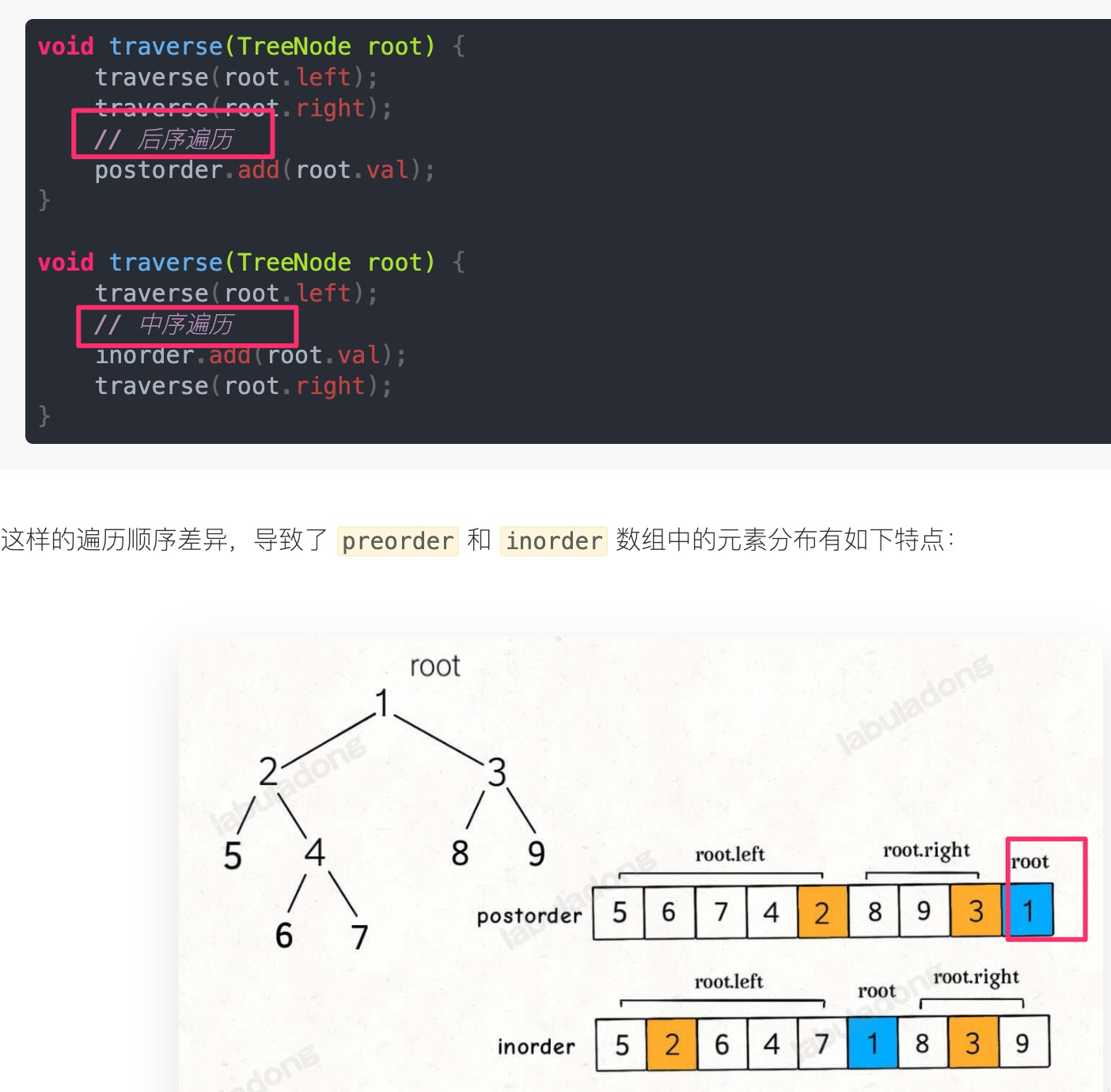
有了前一题的铺垫，这道题很快就解决了，无非就是 rootVal 变成了最后一个元素，再改改递归函数的参数而已，只要明白二叉树的特性，也不难写出来。如下

/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
let valToIndex = new Map();
var buildTree = function(inorder, postorder) {
    for (let i = 0; i < inorder.length; i++) {
        valToIndex.set(inorder[i], i);
    }
    return build(inorder, 0, inorder.length - 1,
                 postorder, 0, postorder.length - 1);
};

function build(inorder,  inStart,  inEnd, 
               postorder, postStart, postEnd) {
        
    if (inStart > inEnd) {
        return null;
    }
    // root 节点对应的值就是后序遍历数组的最后一个元素
    let rootVal = postorder[postEnd];
    // rootVal 在中序遍历数组中的索引
    let index = valToIndex.get(rootVal);
    // 左子树的节点个数
    let leftSize = index - inStart;
    let root = new TreeNode(rootVal,null,null);
    // 递归构造左右子树
    root.left = build(inorder, inStart, index - 1,
                        postorder, postStart, postStart + leftSize - 1);
    
    root.right = build(inorder, index + 1, inEnd,
                        postorder, postStart + leftSize, postEnd - 1);
    return root;
}

5. 通过后序和前序遍历结果构造二叉树

这是力扣第 889 题「 根据前序和后序遍历构造二叉树」，给你输入二叉树的前序和后序遍历结果，让你还原二叉树的结构。

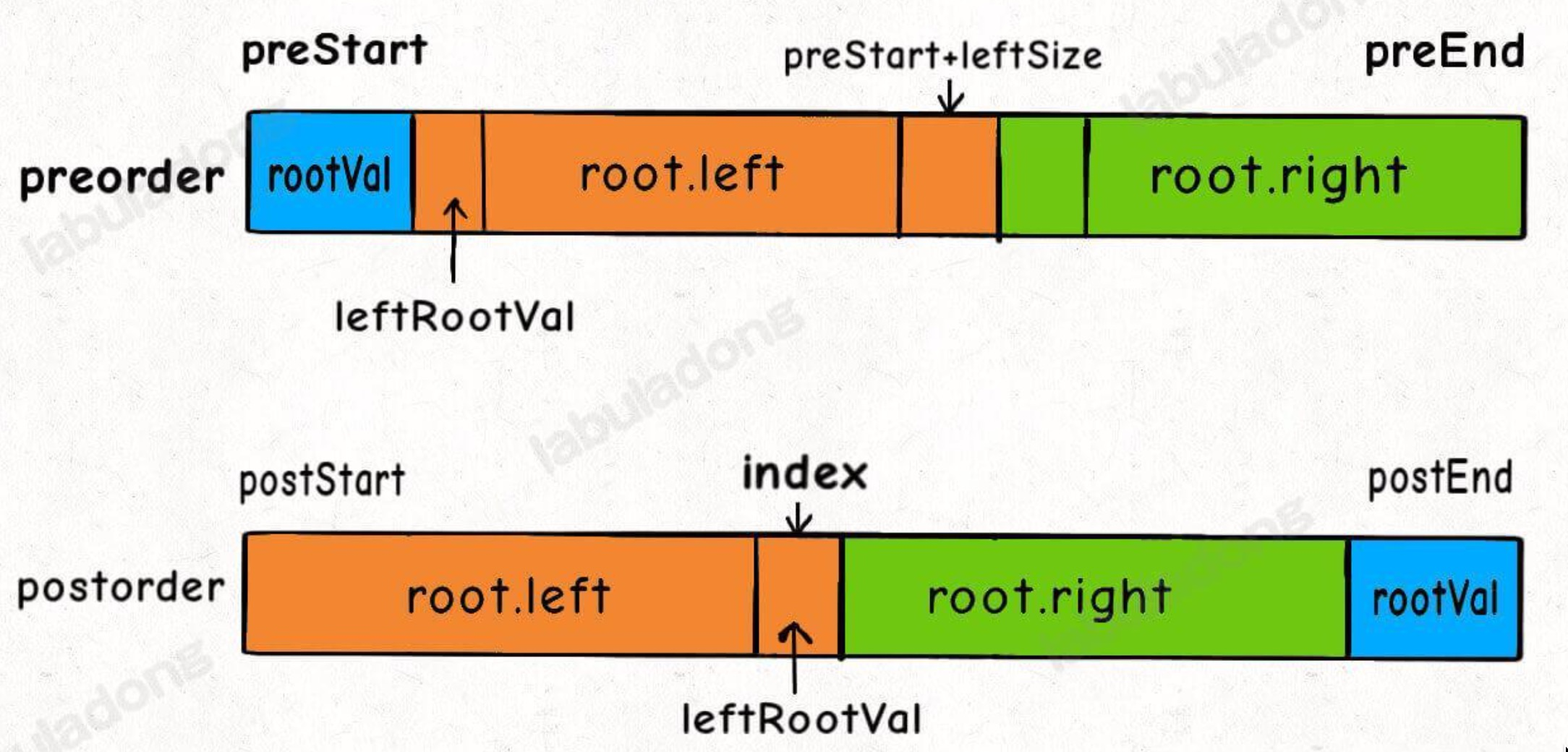
同样的思路：

• 找根节点：
  • 首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素确定为根节点的值
• 构造左、右子树
  • 然后把 前序遍历结果的第二个元素 作为 左子树 的根节点的值
  • 在后序遍历结果中寻找 左子树 根节点的值，从而确定了 左子树 的索引边界，进而确定右子树的索引边界，递归构造左右子树即可。

如下图

代码如下：

/**
 * @param {number[]} preorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */

let valToIndex = new Map();
var constructFromPrePost = function(preorder, postorder) {
    for (let i = 0; i < postorder.length; i++) {
        valToIndex.set(postorder[i], i);
    }
    return build(preorder, 0, preorder.length - 1,
                 postorder, 0, postorder.length - 1);
};
function build( preorder,preStart,preEnd,
                postorder,postStart,postEnd){
        if (preStart > preEnd) {
            return null;
        }
        if (preStart === preEnd) {
            return new TreeNode(preorder[preStart]);
        }
        // root 节点对应的值就是前序遍历数组的第一个元素
        let rootVal = preorder[preStart];
        // root.left 的值是前序遍历第二个元素
        // 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点
        // 确定 preorder 和 postorder 中左右子树的元素区间
        let leftRootVal = preorder[preStart + 1];
        // leftRootVal 在后序遍历数组中的索引
        let index = valToIndex.get(leftRootVal);
        // 左子树的元素个数
        let leftSize = index - postStart + 1;
        // 先构造出当前根节点
        let root = new TreeNode(rootVal,null,null);
        // 递归构造左右子树
        // 根据左子树的根节点索引和元素个数推导左右子树的索引边界
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                postorder, postStart, index);
        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                postorder, index + 1, postEnd - 1);

        return root;
}

为什么不唯一呢？

• 关键这句，int leftRootVal = preorder[preStart + 1]; 我们假设前序遍历的第二个元素是左子树的根节点，但实际上左子树有可能是空指针，那么这个元素就应该是右子树的根节点。由于这里无法确切进行判断，所以导致了最终答案的不唯一

6. 最后

二叉树的构造问题一般都是使用「分解问题」的思路：构造整棵树 = 根节点 + 构造左子树 + 构造右子树