叶子相似的树

#leetcode #算法/二叉树

目录

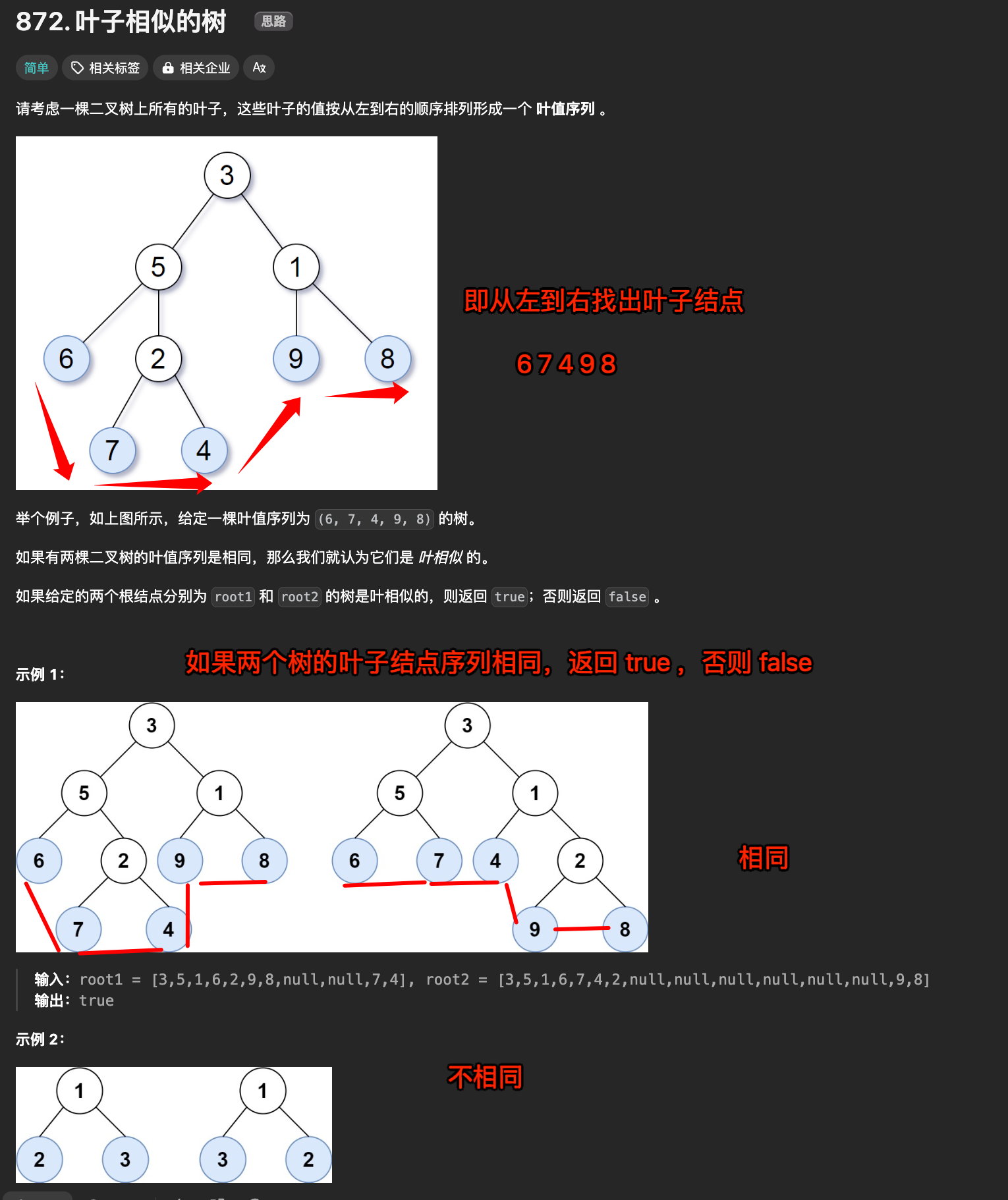
• 1. 题目及理解
• 2. 解题思路
• 3. 代码实现
• 4. 复杂度分析
• 5. 优化建议
• 6. 错误记录

1. 题目及理解

2. 解题思路

1. 分别获取两棵树的叶值序列
   • 遍历一遍树
   • 当遇到叶节点（左右子节点都为空）时，将其值加入序列
2. 比较两个序列是否相同

3. 代码实现

/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {boolean}
 */
var leafSimilar = function (root1, root2) {
    // 获取叶子节点的序列
    const getSeq = (root) => {
        const res = [];
        // 前序遍历
        const traverse = (node) => {
            if (!node) {
                return;
            }
            if (!node.left && !node.right) {
                res.push(node.val);
            }
            traverse(node.left);
            traverse(node.right);
        }
        traverse(root);
        return res;
    }
    const seq1 = getSeq(root1);
    const seq2 = getSeq(root2);
    // 比较两个序列是否相同
    // 如果长度不同，直接返回 false
    if (seq1.length !== seq2.length) {
        return false;
    }
    // 逐个比较, 如果有不同的元素，直接返回 false
    for (let i = 0; i < seq1.length; i++) {
        if (seq1[i] !== seq2[i]) {
            return false;
        }
    }
    // 最后，两个序列完全相同，返回 true
    return true;
};

4. 复杂度分析

• 时间复杂度：O(n1 + n2)
  • n1 和 n2 分别是两棵树的节点数。
  • getSeq 函数对每棵树进行一次完整的遍历，时间复杂度为 O(n)。
    • 对于root1 和 root2，我们分别调用一次getSeq，所以这部分的时间复杂度是 O(n1 + n2)。
  • 最后的比较过程，最坏情况下需要比较所有叶子节点，但这个操作的时间复杂度不会超过 O(min(n1, n2))。
  • 因此，总的时间复杂度是 O(n1 + n2)。
• 空间复杂度：O(h1 + h2 + L)
  • h1 和 h2 分别是两棵树的高度。
  • L 是叶子节点的数量，最坏情况下 L = min(n1, n2)。
  • 递归调用栈的深度最大为树的高度，因此需要 O(h1) 和 O(h2) 的空间。
  • seq1 和 seq2 数组存储叶子节点值，共需要 O(L) 的空间。
  • 因此，总的空间复杂度是 O(h1 + h2 + L)。
• 最坏情况分析：
  • 在最坏情况下，当树完全不平衡（如链状结构）时，h1 可能等于 n1，h2 可能等于 n2。
  • 此时，空间复杂度可能退化为 O(n1 + n2)。
• 平均情况分析：
  • 对于较为平衡的树，h1 和 h2 通常远小于 n1 和 n2。
  • 在这种情况下，空间复杂度会更接近 O(log(n1) + log(n2) + L)。

5. 优化建议

• 可以考虑使用迭代器或生成器来逐个生成和比较叶子节点，而不是先存储完整的序列。
  • 这样可以将空间复杂度降低到 O(h1 + h2)，但可能会稍微增加时间复杂度

6. 错误记录

[!danger] 注意最后返回 ture