迷宫中离入口最近的出口

#leetcode #算法 #图BFS #算法/图 #迷宫问题

目录

• 题目及理解
• 思路
• 代码实现
• 复杂度分析
• 错误记录

题目及理解

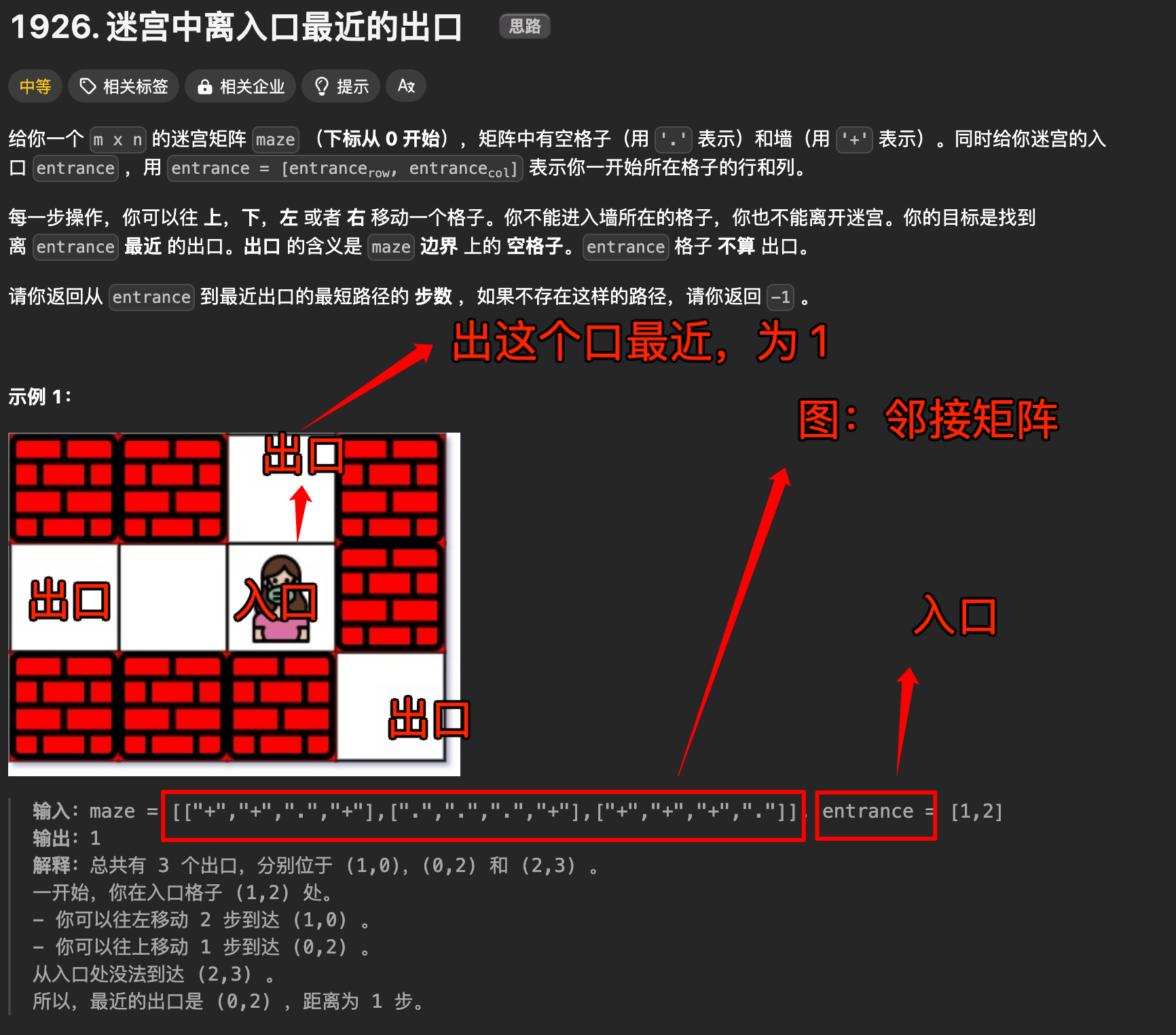
[!danger] 上面的 maza 不是邻接矩阵，m 都不等于 n，邻接矩阵一定是 n*n

思路

这个问题本质上是一个寻找最短路径的问题，通常可以使用广度优先搜索（BFS）来解决。BFS 可以保证首先找到的出口就是最近的出口。

• 关键点
  • 迷宫问题，定义4 个方向，上下左右扩散
  • 初始化 m*n 的 visited 二维数组

代码实现

/**
 * @param {character[][]} maze 邻接矩阵
 * @param {number[]} entrance  出口
 * @return {number}  最少的出口需要走几步
 */
var nearestExit = function (maze, entrance) {
  const m = maze.length;
  const n = maze[0].length;
  // 上下左右四个方向 [x,y]，x 和 y 分别表示横纵坐标的增量
  const dirs = [
    [0, 1], // 向右
    [0, -1], // 向左
    [1, 0], // 向下
    [-1, 0], // 向上
  ];

  // BFS 算法的队列和 visited 数组
  const queue = [];
  // 初始化一个 m * n 的 visited 二维数组
  const visited = Array.from({ length: m }, () => Array(n).fill(false));
  // 将入口放入队列
  queue.push(entrance);
  // 标记入口已访问
  visited[entrance[0]][entrance[1]] = true;
  // 启动 BFS 算法从 entrance 开始像四周扩散
  let step = 0;
  while (queue.length) {
    const sz = queue.length;
    step++;
    // 扩散当前队列中的所有节点
    for (let i = 0; i < sz; i++) {
      // 取出队首节点
      const cur = queue.shift();
      // 每个节点都会尝试向上下左右四个方向扩展一步
      for (const dir of dirs) {
        // cur[0] 和 cur[1] 分别为当前节点的横纵坐标,通过下面的方式计算
        // 上下左右移动后新的坐标
        const x = cur[0] + dir[0];
        const y = cur[1] + dir[1];
        // 如果新坐标 (x, y) 超出边界，或者遇到墙壁，或者已经访问过，都直接跳过
        if (
          x < 0 ||
          x >= m ||
          y < 0 ||
          y >= n ||
          visited[x][y] ||
          maze[x][y] === "+"
        ) {
          continue;
        }
        // 如果走到边界（出口），返回步数
        if (x === 0 || x === m - 1 || y === 0 || y === n - 1) {
          // 走到边界（出口）
          return step;
        }
        // 记录已访问
        visited[x][y] = true;
        // 将新节点加入队列
        queue.push([x, y]);
      }
    }
  }
  return -1;
};

复杂度分析

• 时间复杂度：O(m * n) ，
  • 在最坏的情况下，我们可能需要访问迷宫中的每一个单元格。
  • 平均情况下，由于墙壁的存在，实际访问的单元格数量会少于 m * n
• 空间复杂度：O(m * n)
  1. 主要空间使用：O(m * n)
     • visited 数组：需要 O(m * n) 空间来存储每个单元格的访问状态。
     • 队列：在最坏情况下，可能需要存储所有的 m * n 个单元格。
  2. 其他空间使用：
     • dirs 数组（方向数组）：常数空间 O(1)。
     • 其他变量（如 step, sz 等）：常数空间 O(1)。
  3. 总空间复杂度：O(m * n)
     • 主要由 visited 数组和队列决定。

错误记录

• 别一上来就想着这个 maza 不是邻接矩阵，那么构建一个？
  • 邻接矩阵不好搞，那么直接构建一个邻接表？
• 这题的本质还是迷宫问题，迷宫问题有迷宫问题的套路