不同的二叉搜索树：1-n个数字能构造出多少个 BST

96. 不同的二叉搜索树

目录

• 1. 分析
• 2. 代码
• 3. 加备忘录：否则超时
• 4. 附：n 个节点能组成多少个 BST ？
  • 4.1. 题目
  • 4.2. 解题思路
  • 4.3. 代码
  • 4.4. 优化：使用备忘录
  • 4.5. 动态规划解法

1. 分析

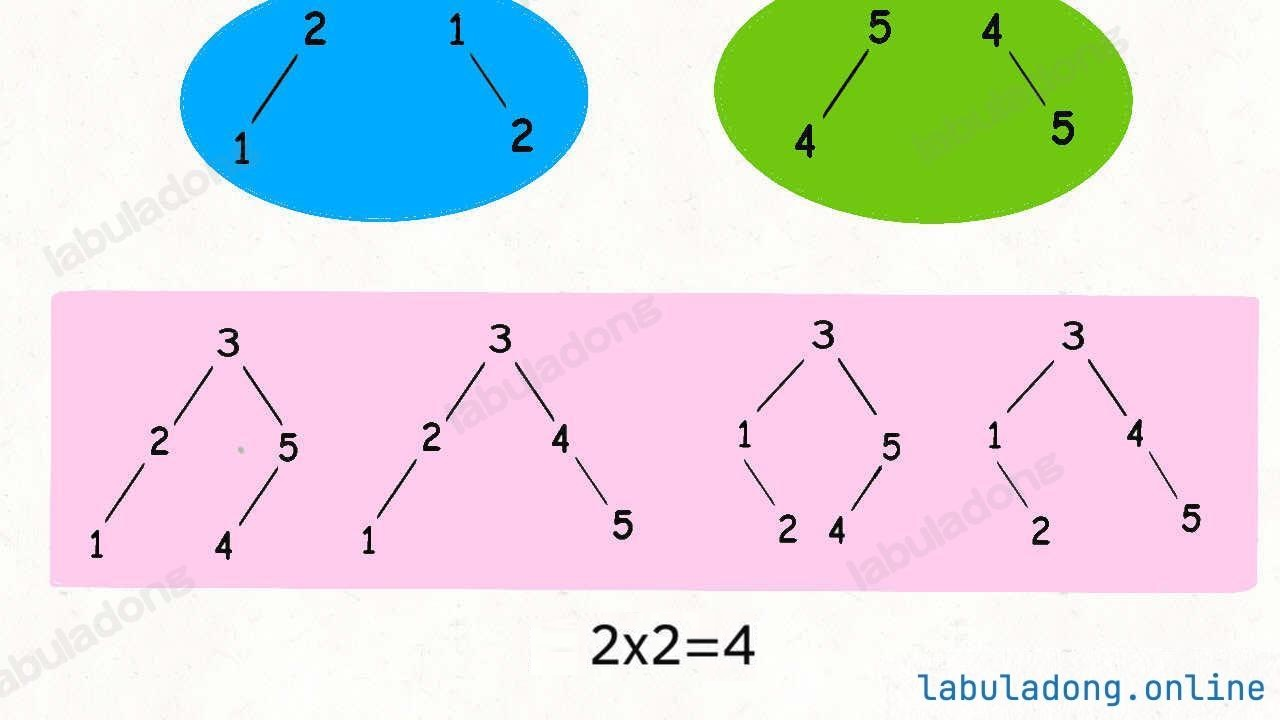
假设给算法输入 n = 5，也就是说用 {1,2,3,4,5} 这些数字去构造 BST。

• 如果固定 3 作为根节点
  • 左子树节点就是 {1,2} 的组合
  • 右子树就是 {4,5} 的组合
• 所以：
  • 左子树的组合数和右子树的组合数乘积就是 3 作为根节点时的 BST 个数

2. 代码

var numTrees = function (n) {
    // 返回 闭区间 [start, end] 组成的 BST 个数
    function count(start, end) {
        if (start > end) return 1; // 即 null
        let res = 0;
        for (let i = start; i <= end; i++) {
            // 根节点：i
            let left = count(start, i - 1);
            let right = count(i + 1, end);
            // 左右子树的组合数乘积是 BST 的总数
            res += left * right;
        }
        return res;
    }
    // 计算闭区间 [1, n] 组成的 BST 个数
    return count(1, n);
};

3. 加备忘录：否则超时

var numTrees = function (n) {
    let memo = {};
    // 返回 闭区间 [start, end] 组成的 BST 个数
    function count(start, end) {
        let key = `${start},${end}`;
        if (memo[key]) return memo[key];
        if (start > end) return 1; // 即 null
        let res = 0;
        for (let i = start; i <= end; i++) {
            // 根节点：i
            let left = count(start, i - 1);
            let right = count(i + 1, end);
            // 左右子树的组合数乘积是 BST 的总数
            res += left * right;
        }
        memo[key] = res;
        return res;
    }

    // 计算闭区间 [1, n] 组成的 BST 个数
    return count(1, n);
};

4. 附：n 个节点能组成多少个 BST ？

4.1. 题目

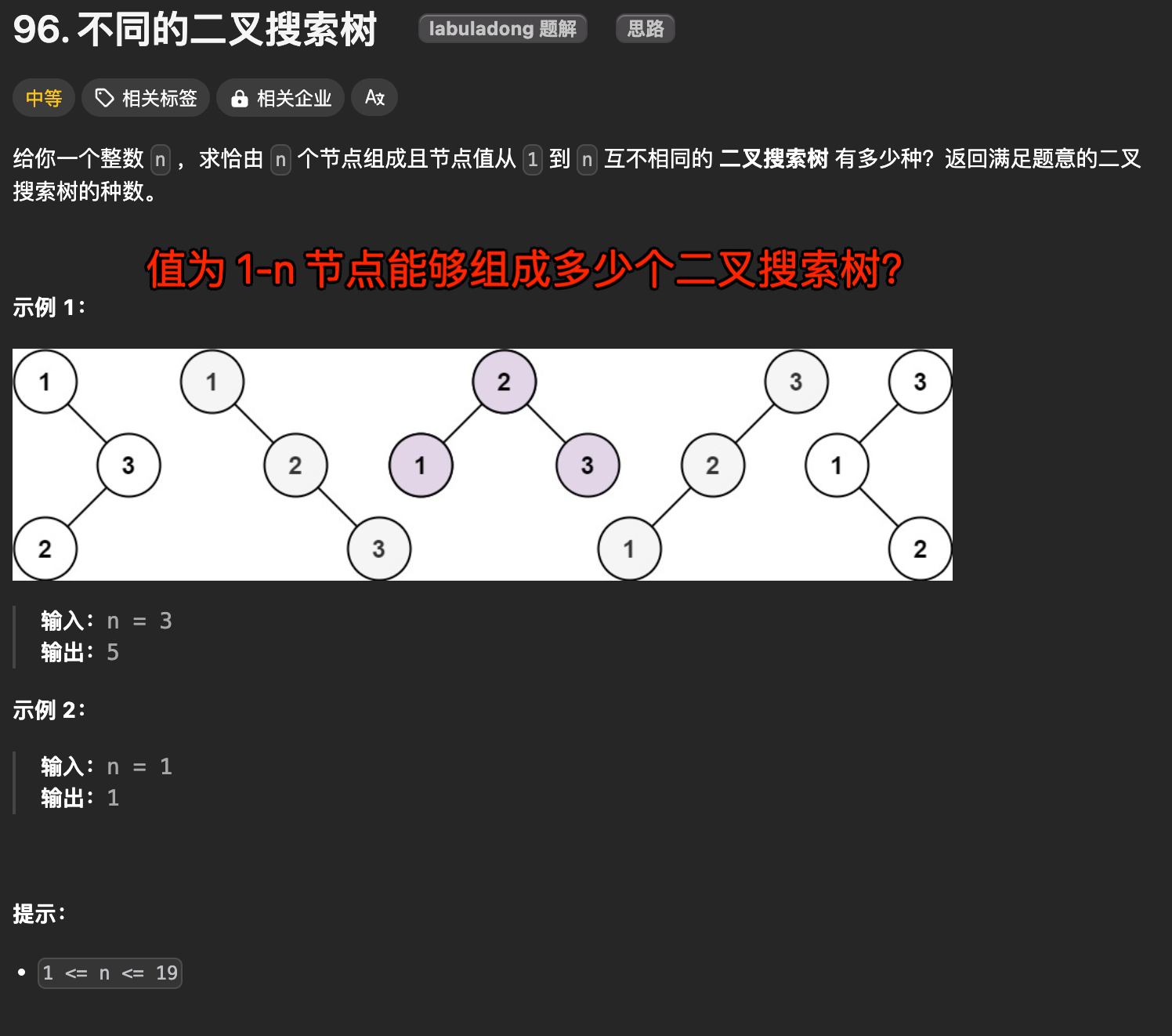
比如，n = 3 时，有 5 种 BST，如下图：

4.2. 解题思路

又比如，n = 5 时，也就是说用 {1,2,3,4,5} 这些数字去构造 BST。

• 根节点总共有有 5 种情况，因为每个数字都可以作为根节点。
  •  3 作为根节点时
    • 左子树节点就是 {1,2} 的组合
    • 右子树就是 {4,5} 的组合
    • 然后 左子树的组合数和右子树的组合数乘积就是 3 作为根节点时的 BST 个数。

基本逻辑写好，然后写个递归，交给递归就行

4.3. 代码

/**
 * @param {number} n
 * @return {number}
 */
var numTrees = function (n) {
  return count(1, n);
};

/**
 * @description [low,high] 范围内构建二叉搜索树的数量
 */
function count(lo, hi) {
  // base case
  // 显然当 lo > hi 闭区间 [lo, hi] 肯定是个空区间，也就对应着空节点 null
  // 虽然是空节点，但是也是一种情况，所以要返回 1 而不能返回 0
  if (lo > hi) {
    return 1;
  }

  let res = 0;

  for (let i = lo; i <= hi; i++) {
    /// 以 root.val = i 时的根节点，左子树的数量
    // 为什么是 i - 1 而不是 i？
    // 因为 i 代表的是根节点的值，所以左子树的范围是 [lo, i - 1]
    let left = count(lo, i - 1);
    /// 以 root.val = i 时的根节点，右子树的数量
    // 为什么 i + 1 而不是 i？
    // 因为 i 代表的是根节点的值，所以右子树的范围是 [i + 1, hi]
    let right = count(i + 1, hi);
    // 以 i 为根节点时，左右子树的组合数量的乘积
    // 就是以 i 为根节点时，BST 的数量
    // 为什么要乘积？
    // 因为对于每个根节点，左右子树的组合数量是独立的
    // 比如说，左子树有 3 种组合，右子树有 5 种组合
    // 那么以当前根节点构建的 BST 就有 3 * 5 = 15 种组合
    res += left * right;
  }

  return res;
}

leetcode上超时了

4.4. 优化：使用备忘录

var numTrees = function (n) {
  // meme[i][j] 代表 i 到 j 的二叉搜索树的个数
  const memo = [];
  for (let i = 0; i < n + 1; i++) {
    memo[i] = [];
    for (let j = 0; j < n + 1; j++) {
      memo[i][j] = 0;
    }
  }
  function count(lo, hi) {
    if (lo > hi) {
      return 1;
    }
    // 先查找备忘录
    if (memo[lo][hi] !== 0) {
      return memo[lo][hi];
    }
    let res = 0;
    for (let i = lo; i <= hi; i++) {
      let left = count(lo, i - 1);
      let right = count(i + 1, hi);
      res += left * right;
    }
    return res;
  }

  return count(1, n);
};

leetcode上还是超时了

4.5. 动态规划解法

var numTrees = function (n) {
  const dp = new Array(n + 1).fill(0);
  // dp[i] 代表 i 个节点的 BST 个数
  // dp[0] = 1, dp[1] = 1 代表空树和一个节点的 BST 个数都是 1
  dp[0] = 1;
  dp[1] = 1;
  // 从 2 开始计算
  for (let i = 2; i <= n; i++) {
    for (let j = 1; j <= i; j++) {
      // j 代表根节点的值
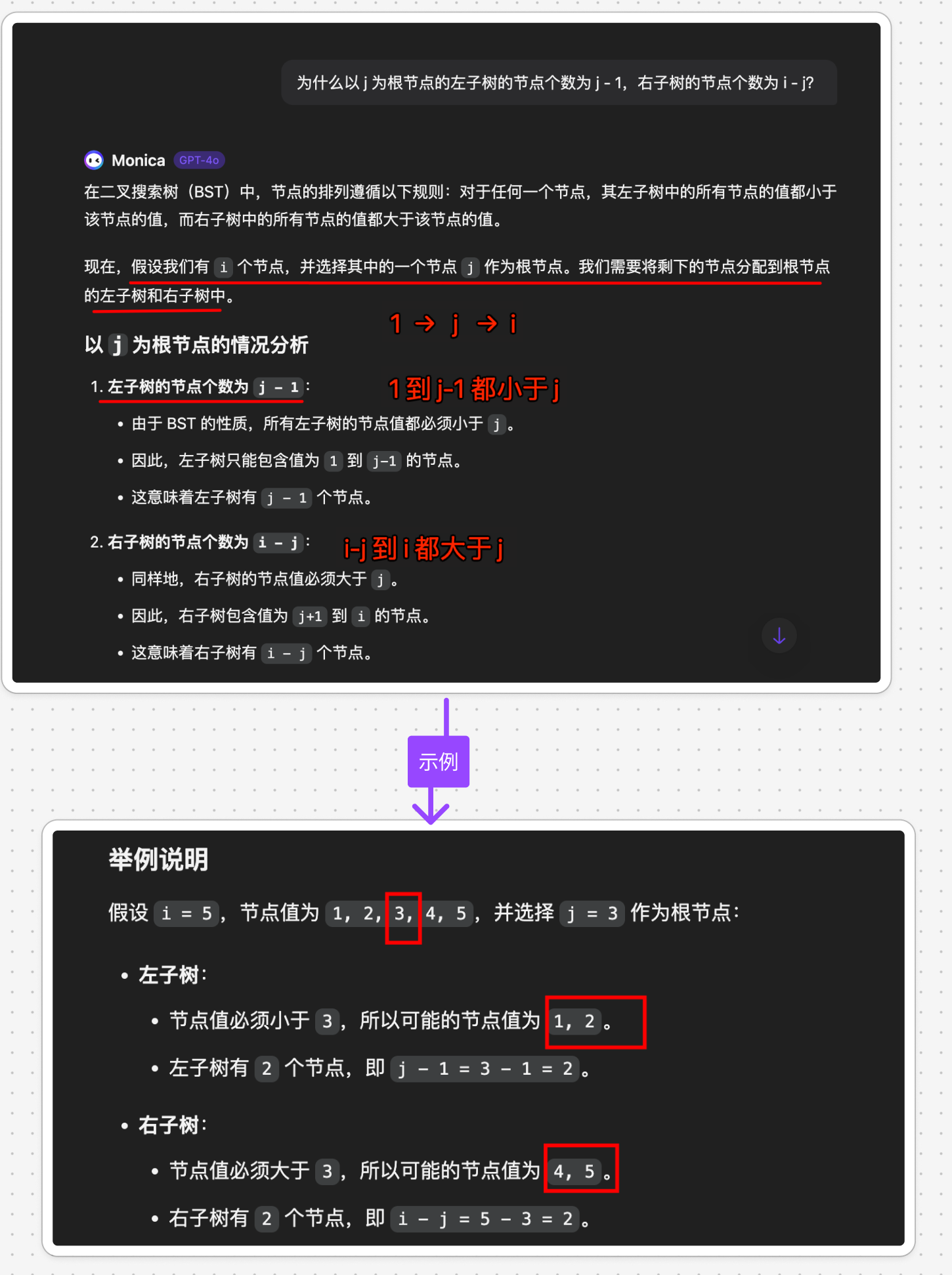
      // 左子树的节点个数为 j - 1, 右子树的节点个数为 i - j ?
      // why? 看后面有截图解释
      // 左子树的 BST 个数为 dp[j - 1], 右子树的 BST 个数为 dp[i - j]
      // 以 j 为根节点的 BST 个数为 dp[j - 1] * dp[i - j]
      dp[i] += dp[j - 1] * dp[i - j];
    }
  }
  return dp[n];
};

能正常通过 leetcode