子序列: 动态规划之子序列问题解题模板(最长回文子序列)
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 1312. Minimum Insertion Steps to Make a String Palindrome | 1312. 让字符串成为回文串的最少插入次数 | 🔴 |
| 516. Longest Palindromic Subsequence | 516. 最长回文子序列 | 🟠 |
目录
1. 子序列不好解决
- 子序列问题本身就相对子串、子数组更困难一些
- 因为序子序列是不连续的
2. 两种解题模板
2.1. 一维 dp 数组
定义:在子数组 arr[0..i] 中,以 arr[i] 结尾的子序列的长度是 dp[i]
这样符合归纳法,可以找到状态转移的关系
int n = array.length;
int[] dp = new int[n];
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
dp[i] = 最值(dp[i], dp[j] + ...)
}
}
注意是上面标注的
j < i
2.2. 二维的 dp 数组
这种思路运用相对更多一些
- 尤其是涉及两个字符串/数组的子序列时
- 在子数组
arr1[0..i]和子数组arr2[0..j]中,我们要求的子序列长度为dp[i][j]- 注意上面的
i 和 j分别代表什么?
- 注意上面的
- 在子数组
- 也可以用于只涉及一个字符串/数组的情景,比如回文子序列问题
- 在子数组
array[i..j]中,我们要求的子序列的长度为dp[i][j]- 注意上面的
i 和 j分别代表什么?
- 注意上面的
- 在子数组
3. 最长回文子序列

比如说输入 s = "aecda",算法返回 3,因为最长回文子序列是 "aca",长度为 3。
3.1. dp 数组定义
dp 数组的定义是:
- 在子串 s[i..j] 中,最长回文子序列的长度为 dp[i][j]
if (s[i] == s[j])
// 它俩一定在最长回文子序列中
dp[i][j] = dp[i + 1][j - 1] + 2;
else
// s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长?
dp[i][j] = max(
dp[i + 1][j],
dp[i][j - 1]
);
3.2. 为什么是 dp[i][j] = dp[i + 1][j - 1]
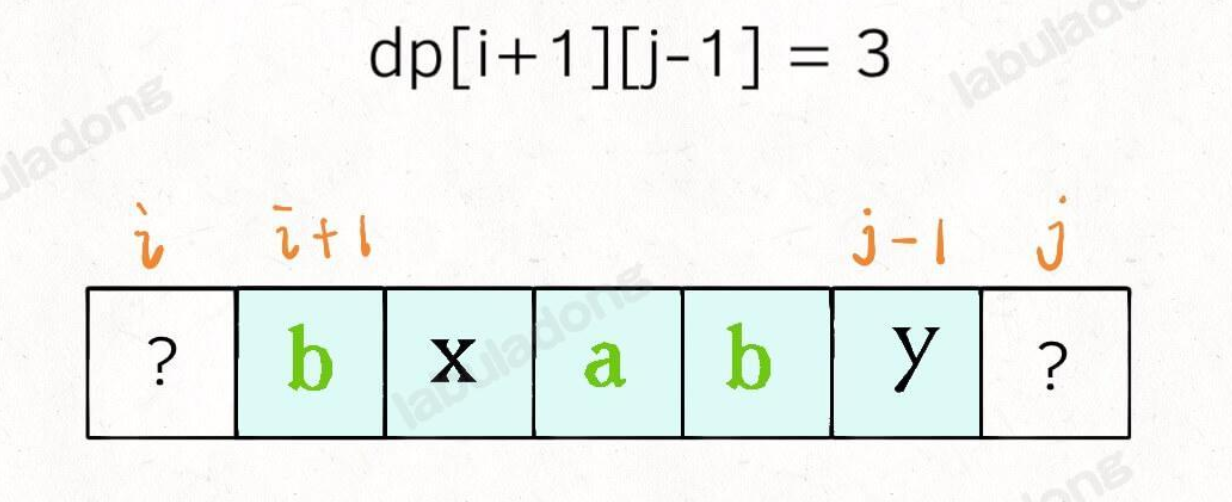
如上图,如果 i=j ,那么就可以
- i 指针向右移动,i + 1
- j 指针向左移动,j - 1
3.3. 遍历顺序
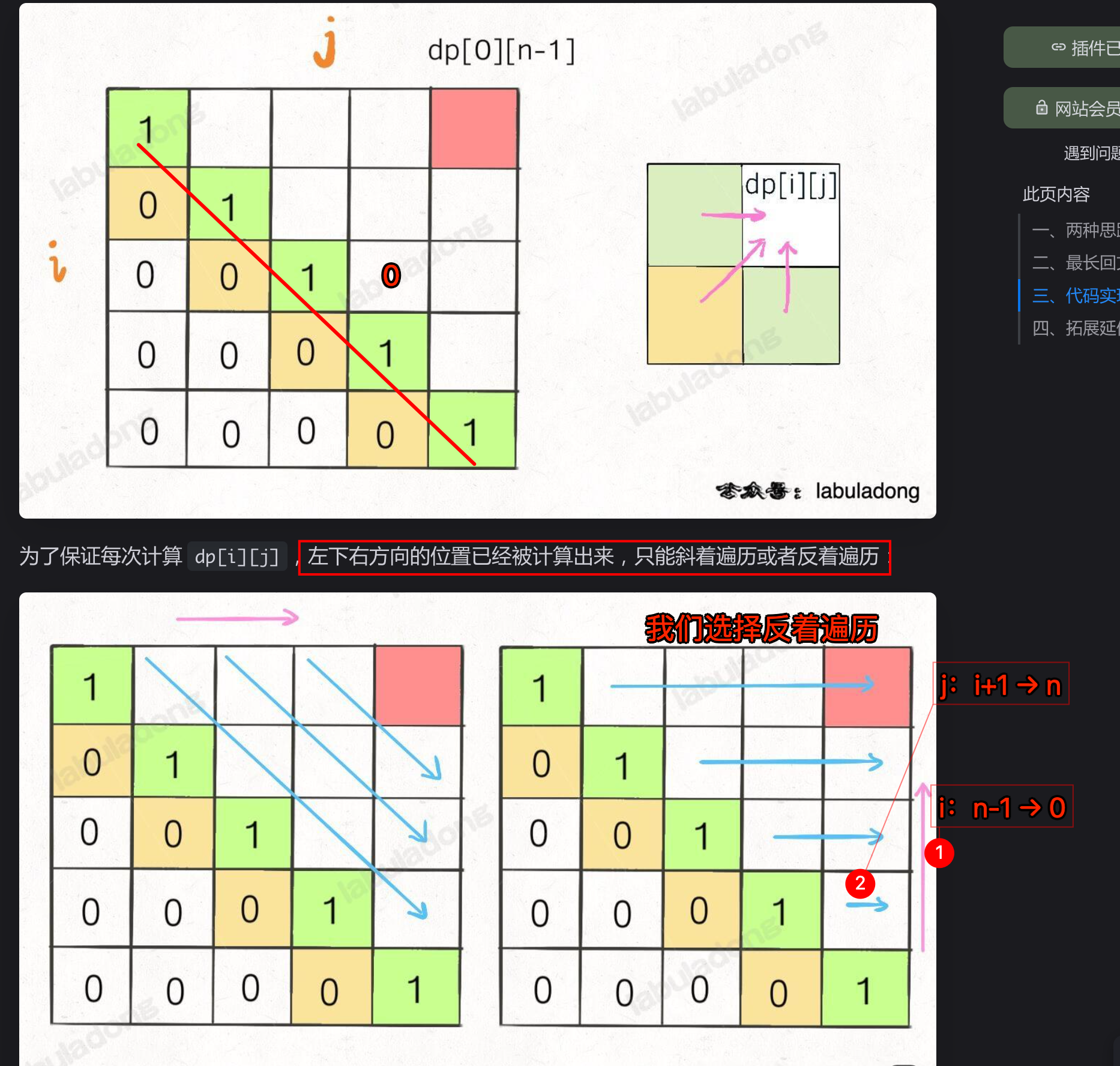
3.4. 最终代码
var longestPalindromeSubseq = function (s) {
var n = s.length;
// dp 数组全部初始化为 0
var dp = Array.from({ length: n }, () => Array(n).fill(0));
// base case:i 和 j 相等的话 dp[i][j] 必然等于 1
// 为什么:因为此时 s[i..j] 只有一个字符,那就是它自己
for (var i = 0; i < n; i++) {
dp[i][i] = 1;
}
// 反着遍历保证正确的状态转移
// 因为 dp[i][j] 依赖 dp[i + 1][j - 1],需要知道 dp[i + 1][j - 1] 才能算出 dp[i][j]
for (var i = n - 1; i >= 0; i--) {
// j 从 i + 1 开始,因为 dp[i][j] 是从 dp[i + 1][j - 1] 转移过来的
for (var j = i + 1; j < n; j++) {
// 状态转移方程
if (s.charAt(i) == s.charAt(j)) {
// s[i] 和 s[j] 必然在最长回文子序列中,直接 +2
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(
dp[i + 1][j], // s[i] 不在最长回文子序列中
dp[i][j - 1], // s[j] 不在最长回文子序列中
);
}
}
}
// 整个 s 的最长回文子串长度
return dp[0][n - 1];
};
4. 让字符串成为回文串的最少插入次数
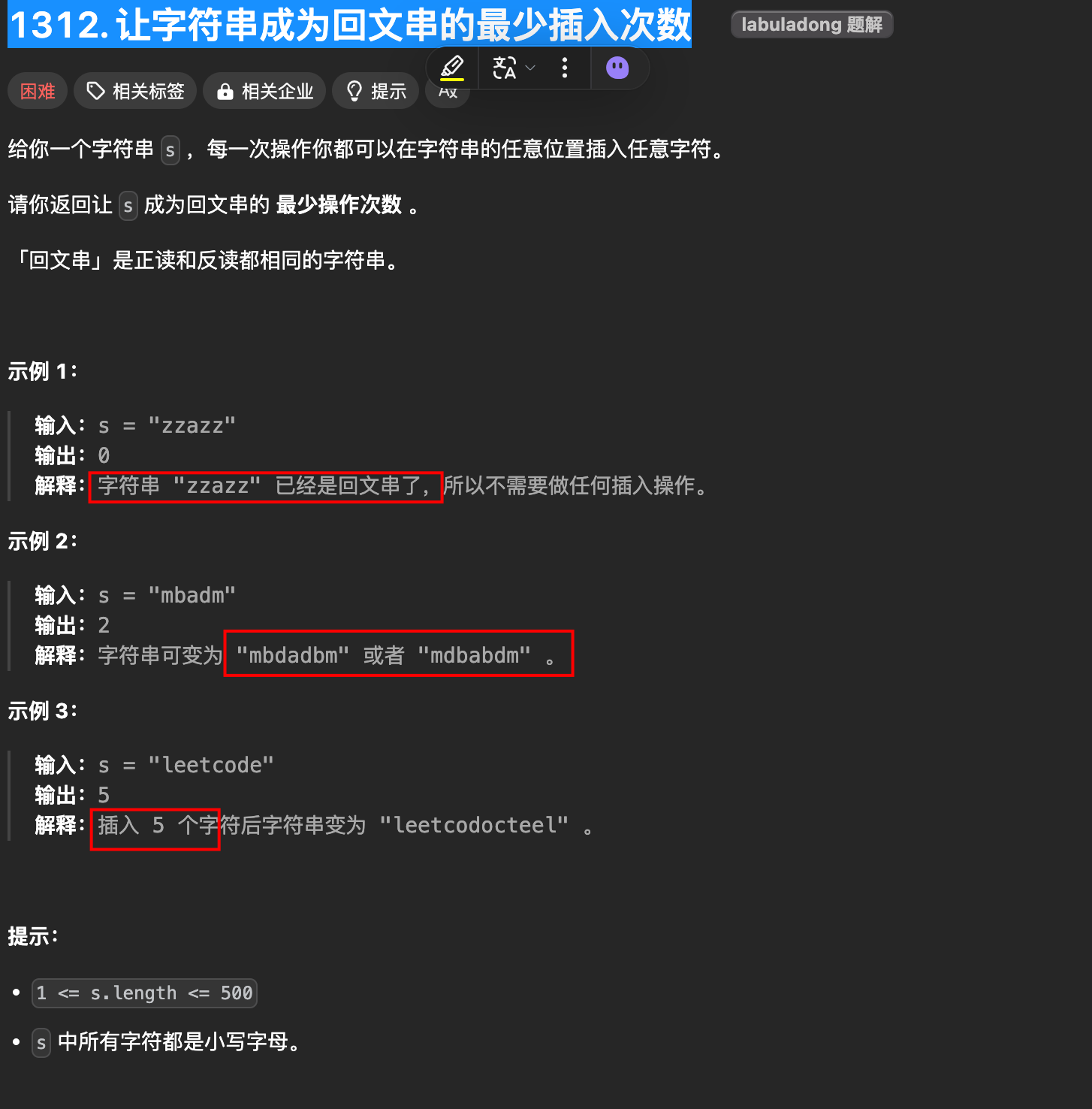
- 比如说输入
s = "abcea",算法返回 2,因为可以给s插入 2 个字符ba变成回文串"abeceba"或者"aebcbea"。 - 如果输入
s = "aba",则算法返回 0,因为s已经是回文串,不用插入任何字符
4.1. dp 定义
对字符串 s[i..j],最少需要进行 dp[i][j] 次插入才能变成回文串
if (s[i] == s[j]) {
// 不需要插入任何字符
dp[i][j] = dp[i + 1][j - 1];
} else {
// 把 s[i+1..j] 和 s[i..j-1] 变成回文串,选插入次数较少的
// 然后还要再插入一个 s[i] 或 s[j],使 s[i..j] 配成回文串
dp[i][j] = min(
dp[i + 1][j], // 再插入一个 s[i]
dp[i][j - 1] // 再插入一个 s[j]
) + 1;
}
4.2. 最终代码
var minInsertions = function (s) {
var n = s.length;
// dp[i][j] 表示把字符串 s[i..j] 变成回文串的最少插入次数
// dp 数组全部初始化为 0
var dp = Array.from(Array(n), () => Array(n).fill(0));
// 反着遍历保证正确的状态转移
for (var i = n - 1; i >= 0; i--) {
for (var j = i + 1; j < n; j++) {
// 状态转移方程
// 如果 s[i] == s[j],说明不用插入,dp[i][j] = dp[i + 1][j - 1]
if (s.charAt(i) === s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1];
} else {
dp[i][j] =
Math.min(
dp[i + 1][j], // 插入 s[i],使得 s[i,j] 变成回文串
dp[i][j - 1], // 插入 s[j],使得 s[i,j] 变成回文串
) + 1;
}
}
}
// 整个 s 的最少插入次数
return dp[0][n - 1];
};
4.3. 复用最长回文子序列的代码
var minInsertions = function(s) {
return s.length - longestPalindromeSubseq(s);
};
// 计算 s 中的最长回文子序列长度
var longestPalindromeSubseq = function(s) {
// 见上文
};