斐波那契数列

#算法/动态规划

虽然它不是动态规划问题，但是对于理解动态规划很有帮助

目录

• 1. 第 509 题
• 2. 自顶向下的暴力递归解法
• 3. 自顶向下的递归解法：带备忘录优化
• 4. 自低向上的迭代解法： dp数组
• 5. 状态转移方程
• 6. 空间复杂度降为 O(1)
• 7. 最后

1. 第 509 题

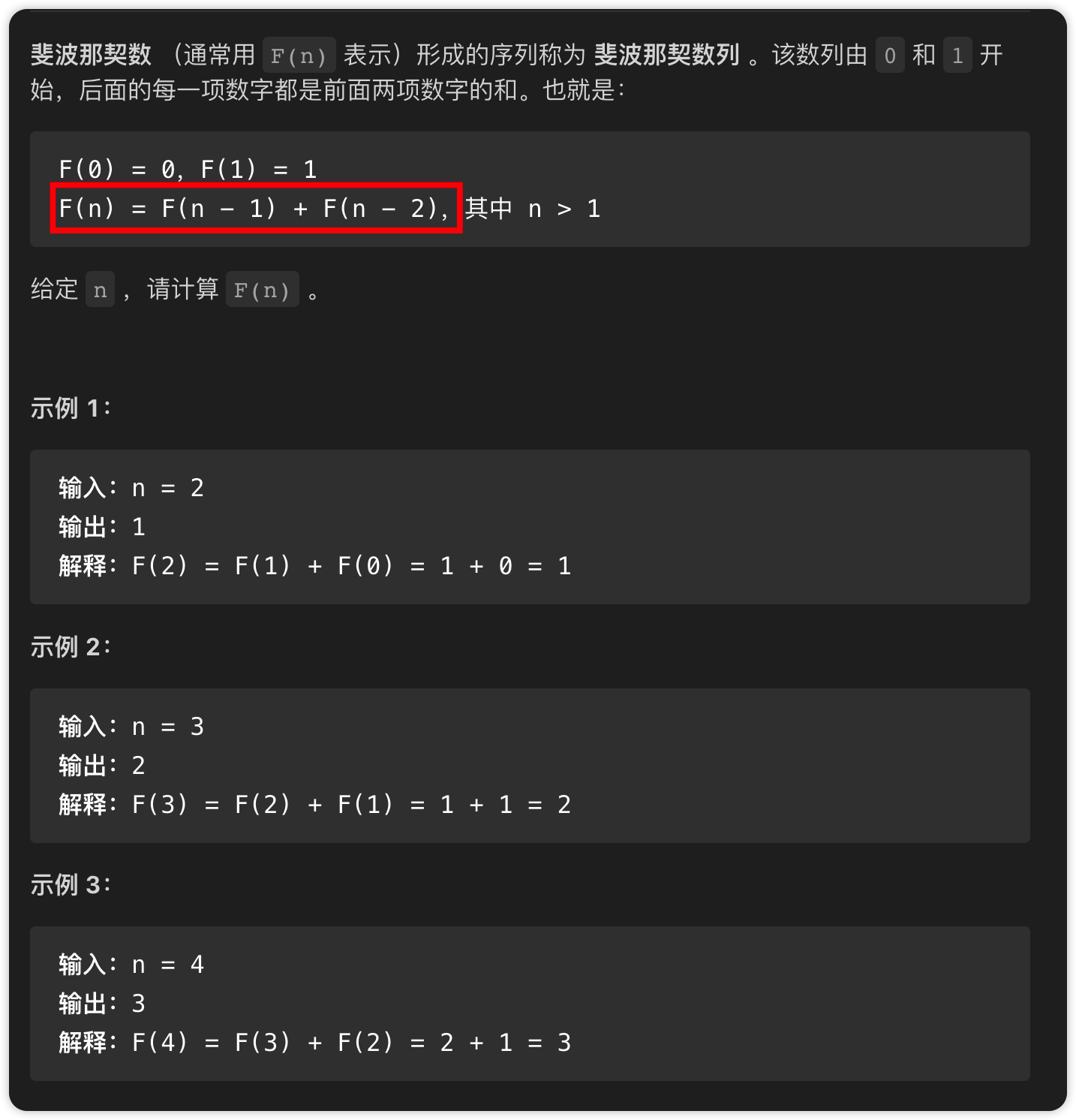
2. 自顶向下的暴力递归解法

var fib = function (n) {
  if (n === 0) return 0;
  if (n === 1) return 1;
  return fib(n - 1) + fib(n - 2);
};

统一尽量使用 dp 函数

/**
 * @param {number} n
 * @return {number}
 */
var fib = function (n) {
  function dp(n) {
    if (n === 0) return 0;
    if (n === 1) return 1;
    return dp(n - 1) + dp(n - 2);
  }
  return dp(n);
};

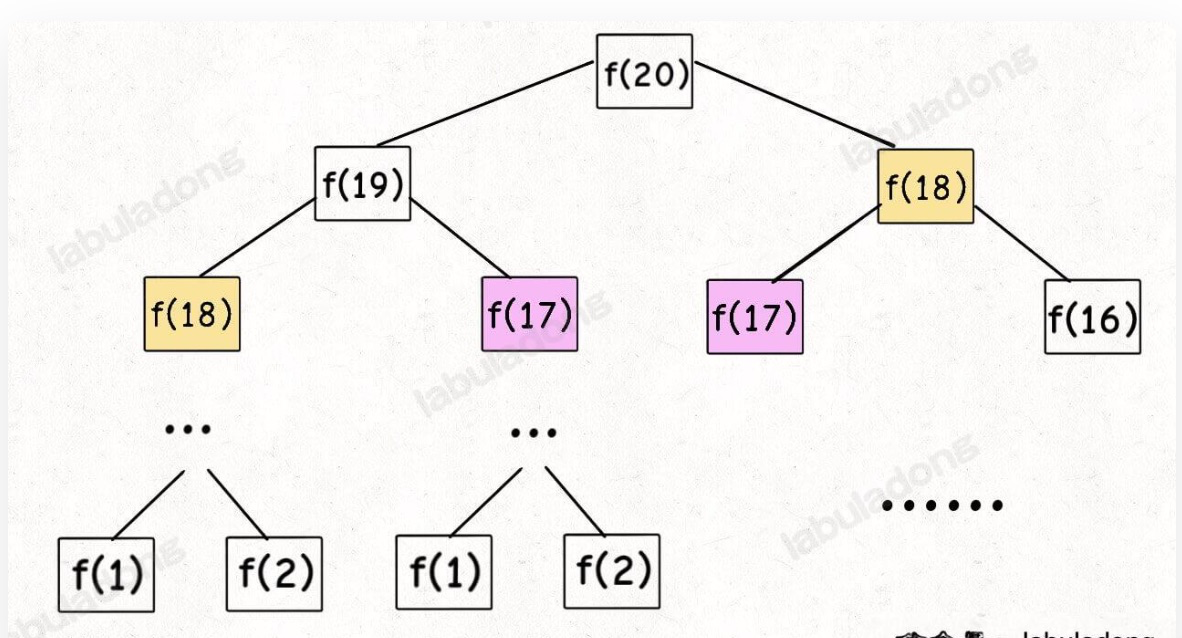
算法复杂度，如下图，即子问题的个数 = O(2^n)  指数级别，爆炸，因为有重叠子问题

3. 自顶向下的递归解法：带备忘录优化

所谓自顶向下，即 原问题 拆解为子问题 ，递归子问题，最终得出原问题的答案

// 解决重叠子问题 - 带备忘录的递归解法
var fib = function (n) {
  // 备忘录全初始化为 0
  let memo = new Array(n + 1).fill(0);
  // 注意，这里利用了闭包，把memo传入，能够保证不销毁
  // 进行带备忘录的递归
  return dp(memo, n);
};
// 带着备忘录进行递归
// 两个参数，传入 memo 数组，添加一个参数
var dp = function (memo, n) {
  // base case
  if (n === 0 || n === 1) return n;
  // 已经计算过，不用再计算了
  if (memo[n] !== 0) return memo[n];
  // 否则，重新计算，并且存到memo中
  // 这里利用了闭包，把memo传入
  memo[n] = dp(memo, n - 1) + dp(memo, n - 2);
  return memo[n];
};

算法的时间复杂度，即 子问题的个数 = O(n) ， 空间复杂度 O(n)

更简单的写法是：dp 函数写到函数体里面，传入参数少一点

/**
 * @param {number} n
 * @return {number}
 */
var fib = function (n) {
  let memo = new Array(n + 1).fill(-1);
  function dp(n) {
    if (n === 0) return 0;
    if (n === 1) return 1;
    if (memo[n] !== -1) return memo[n];
    let res = dp(n - 1) + dp(n - 2);
    memo[n] = res;
    return res;
  }
  return dp(n);
};

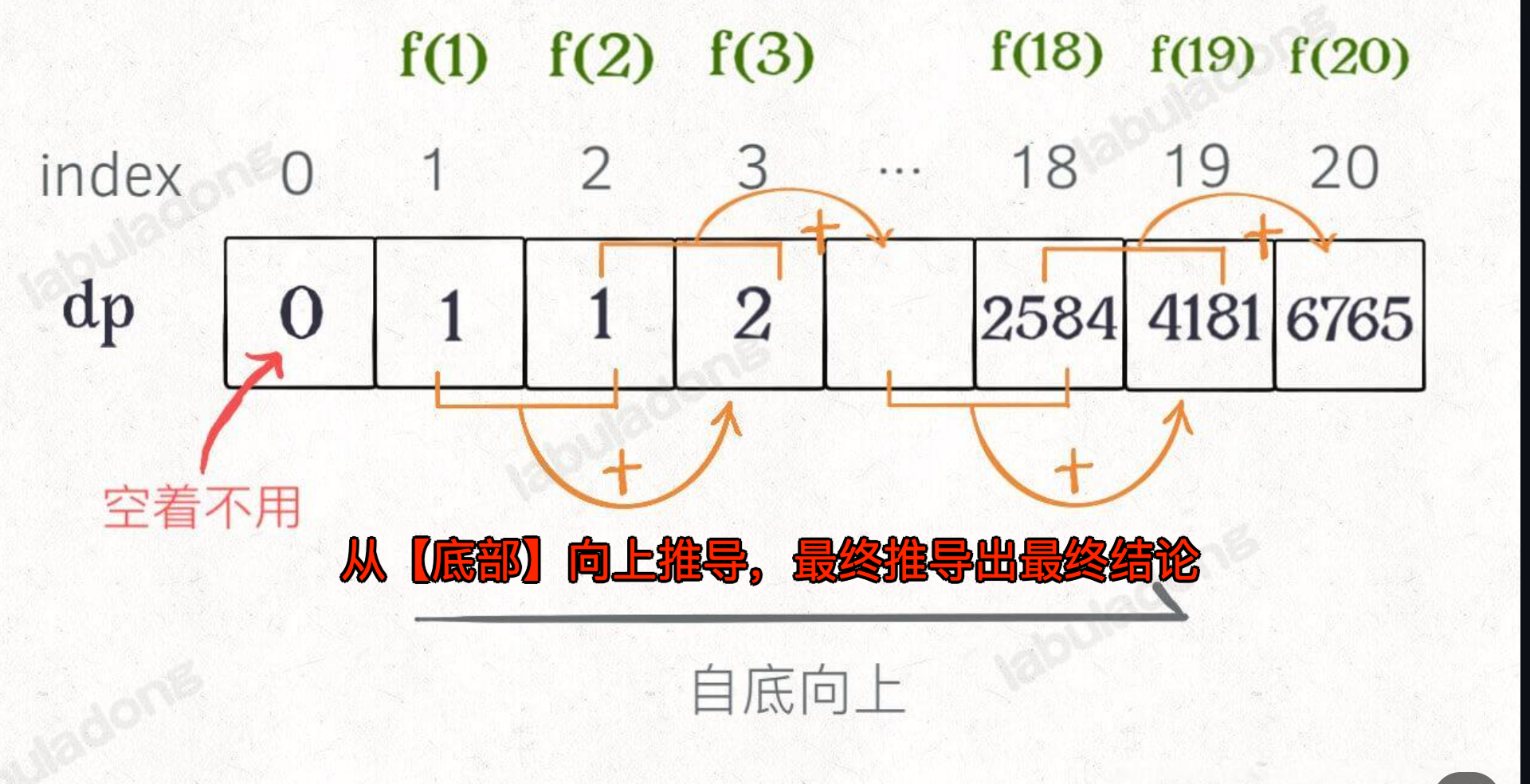
如下图：

4. 自低向上的迭代解法： dp数组

/**
 * @param {number} n
 * @return {number}
 */
var fib = function (n) {
  let dp = new Array(n).fill(-1);
   // base cade
  dp[0] = 0;
  dp[1] = 1;
  // 状态转移方程
  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
};

算法的时间复杂度是O(n) ，空间复杂度O(n)

5. 状态转移方程

其实，就是转态转移方程的实现，如下：

6. 空间复杂度降为 O(1)

// 进一步优化，把二维的dp table 压成一维的,即只要维护两个变量 prev  curr
function fib (n) {
  if (n === 0 || n === 1) return n;
  let prev = 1, curr = 1;
  
  for (let i = 2; i < n; i++) {
    let sum = prev + curr;
    prev = curr;
    curr = sum;
  }

  return curr;
};

7. 最后

1. dp数组解法可能进一步压缩空间复杂度，而通过递归函数解法不一定能够压缩
2. 说说 dp数组 与 dp函数 区别 ？