买卖股票的最佳时机 IV
#leetcode #2024/08/10 #算法/动态规划
目录
题目及理解
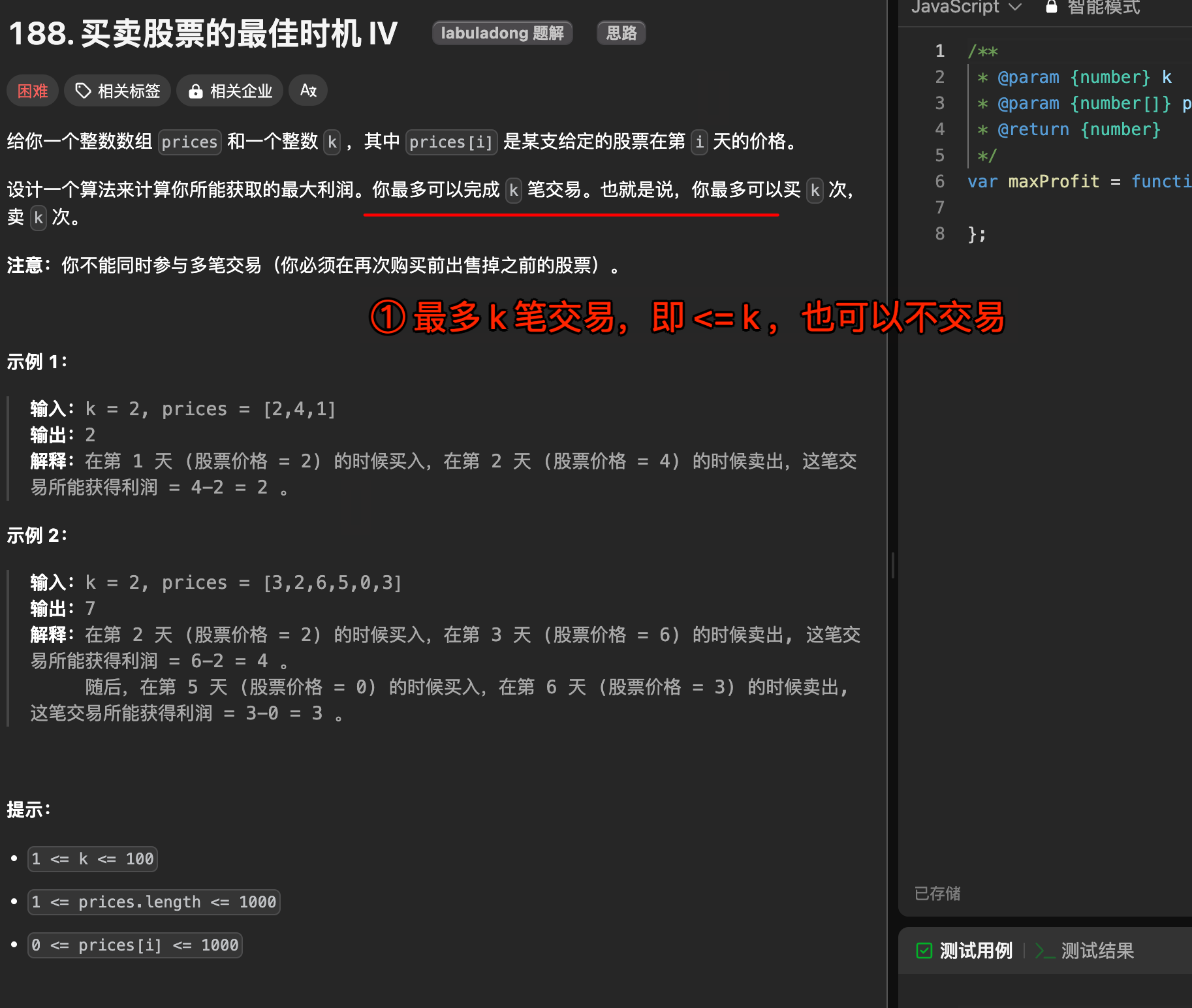
这题是股票买卖最通用的一题,可以以他基准解决其他股票相关的问题,如下图
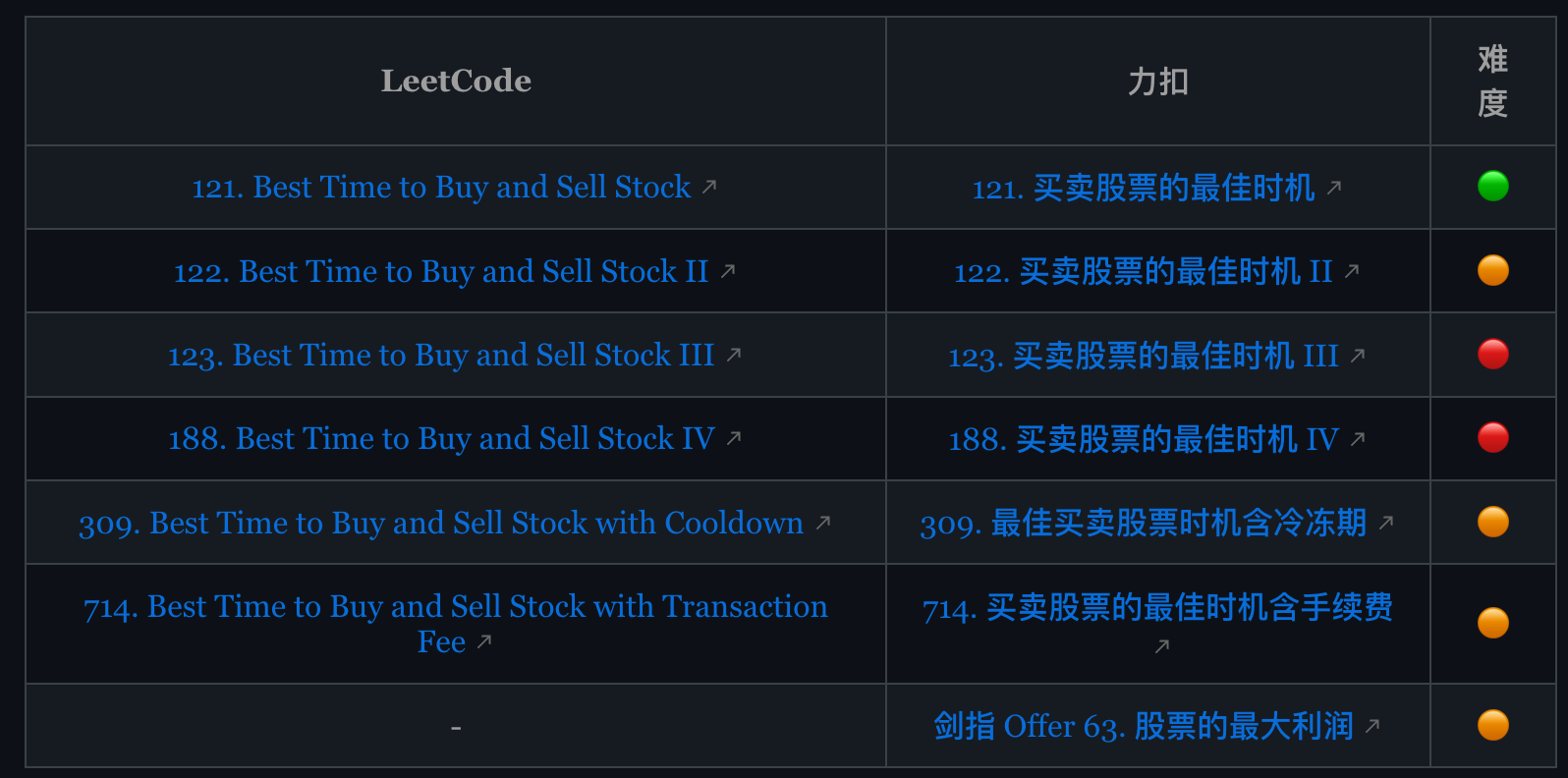
- 第一题是只进行一次交易,相当于
k = 1; - 第二题是不限交易次数,相当于
k = +infinity(正无穷); - 第三题是只进行 2 次交易,相当于
k = 2; - 剩下两道也是不限次数,但是加了交易「冷冻期」和「手续费」的额外条件,其实就是第二题的变种,都很容易处理
解题思路
思路一:动态规划
框架:明确状态和选择
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)
- 选择:每天都有三种选择:买入、卖出、无操作
- 用
buy,sell,rest表示这三种选择。
- 用
- 状态:这个问题的「状态」有三个,所以可以使用
三维数组来组装下所有组合- ① 第一个是
天数 - ② 第二个是
允许交易的最大次数 - ③ 第三个是
当前的持有状态- 即之前说的
rest的状态- 用
1表示持有 0表示没有持有
- 用
- 即之前说的
- ① 第一个是
再看最新的框架
dp[i][k][0 or 1]
① i: 0 <= i <= n - 1 , n 表示 `天数`
② k: 1 <= k <= K ,K 表示`允许交易的最大次数`
③ 0 or 1 : 代表`当前的持有状态` , 0 和 1 代表是否持有股票。
所以 此问题共 n × K × 2 种状态,全部穷举就能搞定。
for 0 <= i < n:
for 1 <= k <= K:
for s in {0, 1}:
dp[i][k][s] = max(buy, sell, rest)
举例:
- dp[3][2][1] 的含义就是:今天是第三天,我现在手上持有着股票,至今最多还可以进行 2 次交易。
- dp[2][3][0] 的含义:今天是第二天,我现在手上没有持有股票,至今最多还可以进行 3 次交易
我们想求的最终答案是 dp[n - 1][K][0],即最后一天,最多允许 K 次交易,最多获得多少利润。
读者可能问为什么不是 dp[n - 1][K][1]?
- 因为
dp[n - 1][K][1]代表到最后一天手上还持有股票 dp[n - 1][K][0]表示最后一天手上的股票已经卖出去了- 很显然后者得到的利润一定大于前者
状态转移框架
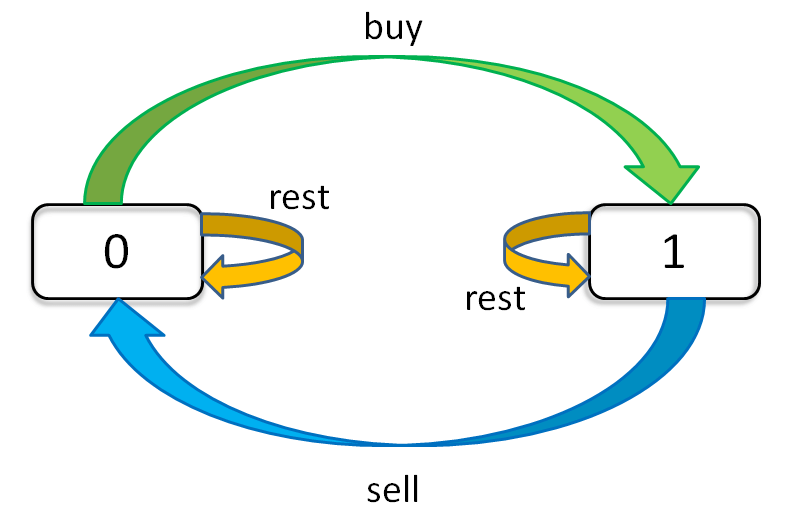
今天没有持有股票: dp[i][k][0]
- 昨天没有持有,今天选择不买,
k不会变 - 昨天持有,今天选择卖掉,
k不会变
// 今天我没有持有股票,有两种可能,我从这两种可能中求最大利润,如下代码:
dp[i][k][0] = max( ① dp[i-1][k][0], ② dp[i-1][k][1] + prices[i] )
= max( ① 昨天没有持有,今天选择不买 ② 昨天持有,今天选择卖掉 sell )
① dp[i-1][k][0] ,即我昨天就没有持有,且截至昨天最大交易次数限制为 k;然后我今天选择 rest,所以我今天还是没有持有,最大交易次数限制依然为 k
② dp[i-1][k][1] + prices[i] ,我昨天持有股票,且截至昨天最大交易次数限制为 k;但是今天我 sell 了,所以我今天没有持有股票了,最大交易次数限制依然为 k
今天持有股票: dp[i][k][1]
- 昨天持有,今天还是继续持有,
k不变 - 昨天没有持有,今天选择买,
k从k-1而来
dp[i][k][1] = max( ① dp[i-1][k][1], ② dp[i-1][k-1][0] - prices[i] )
max( ① 昨天持有,今天还是继续持有, ② 昨天没有持有,今天选择买 )
① dp[i-1][k][1] ,我昨天就持有着股票,且截至昨天最大交易次数限制为 k;然后今天选择 rest,所以我今天还持有着股票,最大交易次数限制依然为 k。
② dp[i-1][k-1][0] - prices[i] 我昨天本没有持有,且截至昨天最大交易次数限制为 k - 1;但今天我选择 buy,所以今天我就持有股票了,最大交易次数限制为 k。
注意点
- 如果
buy,就要从利润中减去prices[i] - 如果
sell,就要给利润增加prices[i]。 - 今天的最大利润就是这两种可能选择中较大的那个。
- 注意
k的限制,在选择buy的时候相当于开启了一次交易,那么对于昨天来说,交易次数的上限k应该减小 1。
base case
dp[-1][0 ~ k][0] = 0
解释:因为 i 是从 0 开始的,所以 i = -1 意味着还没有开始,这时候的利润当然是 0。
dp[-1][0 ~ k][1] = -infinity
解释:还没开始的时候,是不可能持有股票的。
因为我们的算法要求一个最大值,所以初始值设为一个最小值,方便取最大值。
dp[...][0][0] = 0
解释:因为 k 是从 1 开始的,所以 k = 0 意味着根本不允许交易,这时候利润当然是 0。
dp[...][0][1] = -infinity
解释:不允许交易的情况下,是不可能持有股票的。
因为我们的算法要求一个最大值,所以初始值设为一个最小值,方便取最大值。
最后总结
base case:
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity
状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
代码实现
/**
* @param {number} k
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function (k, prices) {
let n = prices.length;
// 利润
let res = 0;
// 如果 n 为 0,返回 0, 无需交易,利润为 0
// 如果 k 为 0,返回 0, 无法交易,利润为 0
if (n === 0 || k === 0) {
return 0;
}
// 初始化 dp 数组,三维数组
// dp[i][k][0/1] 表示第 i 天,最多进行 k 次交易,持有/不持有股票时的利润
let dp = [];
for (let i = 0; i < n; i++) {
dp[i] = [];
for (let j = 0; j <= k; j++) {
dp[i][j] = [];
for (let l = 0; l < 2; l++) {
dp[i][j][l] = 0;
}
}
}
// base case 1
// 如果 k 为 0 , 且没有股票,利润为 0
// 如果 k 为 0, 且有股票,利润为 -Infinity,用于表示不可能的情况,方便后续取最大值
for (let i = 0; i < n; i++) {
dp[i][0][0] = 0;
dp[i][0][1] = -Infinity;
}
// 遍历 prices
for (let i = 0; i < n; i++) {
for (let j = 1; j <= k; j++) {
// base case, i 为 -1 时,越界
if (i === 0) {
dp[i][j][0] = 0;
dp[i][j][1] = -prices[i];
continue;
}
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
res = Math.max(dp[n - 1][k][0], dp[n - 1][k][1]);
// 返回最大利润
return res;
};
复杂度分析
- 时间复杂度:
O(n * k)- 我们有两个主要的嵌套循环:
- 外层循环遍历
prices数组,共n次; - 内层循环遍历
k次交易。
- 外层循环遍历
- 在每次循环中,我们进行常数次操作(比较和赋值)。
- 因此,总的时间复杂度是
O(n * k)。
- 我们有两个主要的嵌套循环:
- 空间复杂度:
O(n * k)- 我们使用了一个三维数组 dp,其大小为
n * (k+1) * 2。 - 虽然最后一个维度是
常数(2),但在大 O 表示法中我们通常忽略常数因子。 - 因此,空间复杂度为
O(n * k)
- 我们使用了一个三维数组 dp,其大小为
思路二
代码实现
复杂度分析
错误记录一
需要移除了 dp[-1] 的初始化,因为这在 JavaScript 中是无效的,在遍历时特殊处理吧,如下图
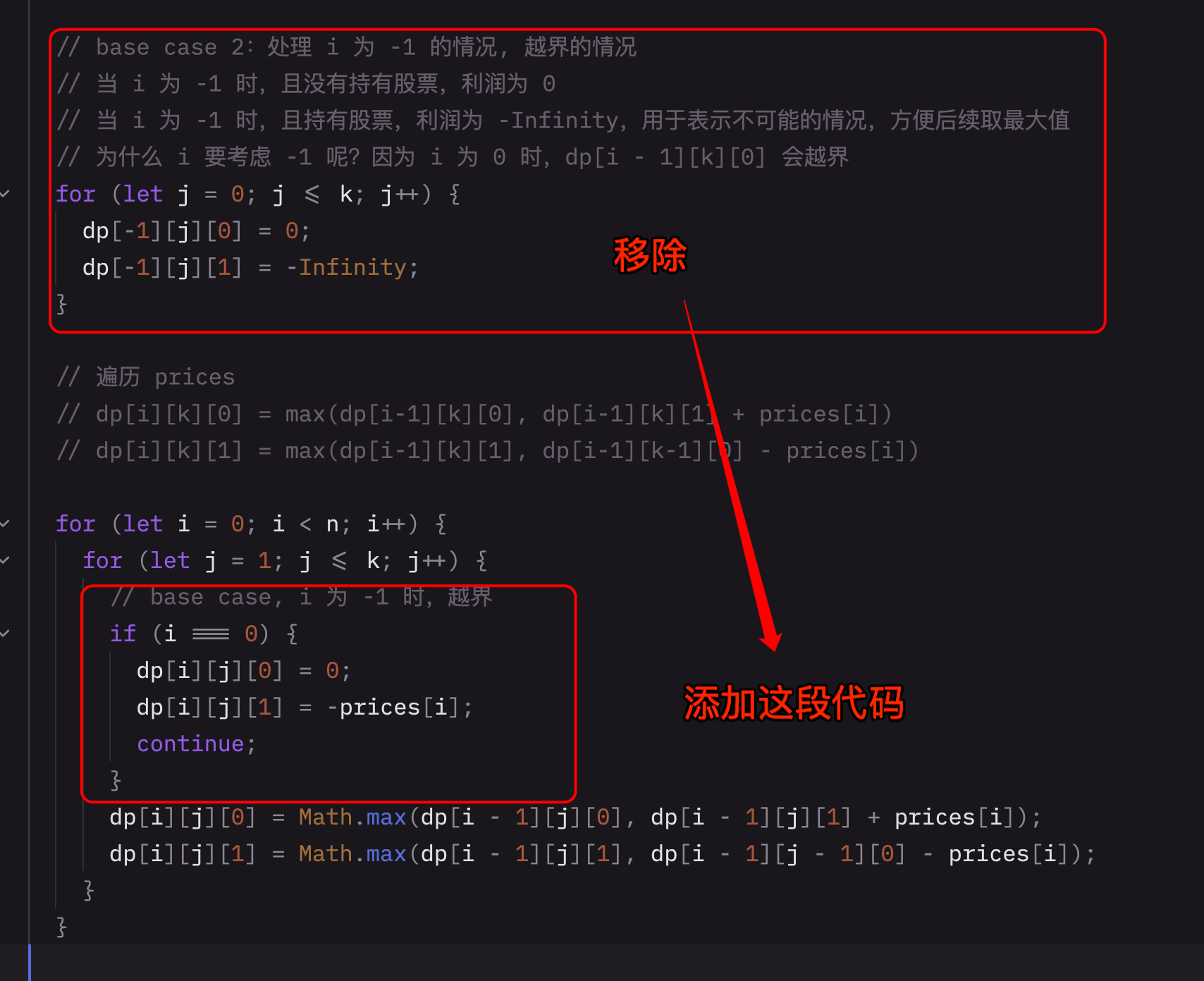
错误记录二
初始化一个二维数组或者三维数组,别使用 Array.form({lenght:n}) 之类的了,使用下面代码肯定不会出问题
// 初始化 dp 数组,三维数组
// dp[i][k][0/1] 表示第 i 天,最多进行 k 次交易,持有/不持有股票时的利润
let dp = [];
for (let i = 0; i < n; i++) {
dp[i] = [];
for (let j = 0; j <= k; j++) {
dp[i][j] = [];
for (let l = 0; l < 2; l++) {
dp[i][j][l] = 0;
}
}
}