通过自注意力机制关注输入的不同部分

#2026/01/02 #ai

作为程序员，你可以把 “自注意力（Self-Attention）” 理解为一种 “加权平均” 算法

它的核心目标是：让输入序列中的每个元素，都有机会“看一眼”序列中的其他所有元素，然后根据相关性（相似度）来更新自己的表示。

这一节我们实现的是一个简化版（没有可训练权重矩阵 $W_q, W_k, W_v$）的自注意力，这是理解后续完整版的必经之路。

目录

• 1. 核心目标：计算上下文向量 (Context Vector)
  • 总结
• 2. 代码实战：逐步实现
  • 准备数据
  • 2.1 第一步：计算注意力分数 (Attention Scores)
  • 2.2 第二步：计算注意力权重 (Attention Weights)
  • 2.3 第三步：计算上下文向量 (Context Vector)
• 3. 进阶：向量化实现
  • 3.1 计算所有对所有 (All-to-All) 的分数
  • 3.2 归一化权重
  • 3.3 计算所有上下文向量
• 4. 总结：这节课学了什么？

1. 核心目标：计算上下文向量 (Context Vector)

假设输入一句话：“Your journey starts with one step.”。

在这句话里，“journey” 和 “starts” 可能关系紧密，和 “one” 关系较远。

自注意力机制就是要计算出一个上下文向量 $z$，这个向量是所有输入单词向量的加权和。

• 输入： $x^{(1)}, x^{(2)}, \dots, x^{(T)}$ （$T$ 个单词的嵌入向量）
• 输出： $z^{(1)}, z^{(2)}, \dots, z^{(T)}$ （包含了上下文信息的向量）

[!question]
针对每个单词，都会重新计算一遍？

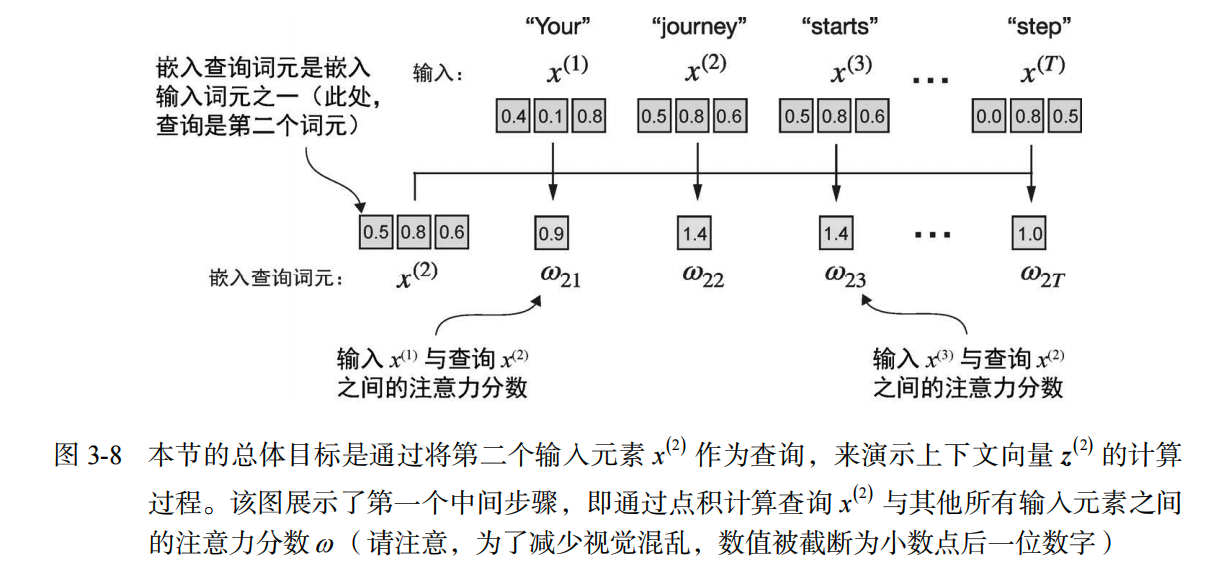
下图以 journey 为例，计算上下文向量 z2

自注意力机制的目标是为每个输入元素计算一个上下文向量，该向量结合了其他所有输入元素的信息。在该图的示例中，我们计算了上下文向量 。计算 时，各个输入元素的重要性或贡献度由注意力权重 到 决定。这些注意力权重是针对输入元素及其他所有输入元素计算的

总结

上下文向量 （context vector）可以被理解为一种包含了序列中所有元素信息的嵌入向量。

2. 代码实战：逐步实现

为了方便演示，我们假设输入句子有 6 个单词，每个单词已经被嵌入成了一个 3 维向量（d_in=3）。

肯定不是 3 维，这里只是为了示例说明

准备数据

import torch

# 模拟输入：6个单词，每个单词是3维向量
# 对应句子: "Your journey starts with one step"
inputs = torch.tensor(
  [[0.43, 0.15, 0.89], # Your     (x^1)
   [0.55, 0.87, 0.66], # journey  (x^2)
   [0.57, 0.85, 0.64], # starts   (x^3)
   [0.22, 0.58, 0.33], # with     (x^4)
   [0.77, 0.25, 0.10], # one      (x^5)
   [0.05, 0.80, 0.55]] # step     (x^6)
)

print(f"输入形状: {inputs.shape}")
# 输出: 输入形状: torch.Size()

2.1 第一步：计算注意力分数 (Attention Scores)

我们想知道第 2 个单词 “journey” ($x^{(2)}$) 和其他单词有多相关。 在数学上，点积 (Dot Product) 是衡量两个向量相似度的 好工具。

• Query (查询): $x^{(2)}$ (journey)
• Key (键): 所有的输入向量 $x^{(1)} \dots x^{(6)}$

代码实现（针对第 2 个输入）：

# 选定第2个输入作为“查询”（Query）
query = inputs

# 创建一个空的容器来存分数
attn_scores_2 = torch.empty(inputs.shape)

# 遍历所有输入，计算它们与 query 的点积
for i, x_i in enumerate(inputs):
    # 点积操作：衡量向量相似度
    attn_scores_2[i] = torch.dot(x_i, query)

print("注意力分数 (针对 input):", attn_scores_2)

执行结果：

注意力分数 (针对 input): 
tensor([0.9544, 1.4950, 1.4754, 0.8434, 0.7070, 1.0865])

1.4950 是自己和自己的点积，通常大。1.4754 对应 “starts”，分数也很高，说明它们很相关。

2.2 第二步：计算注意力权重 (Attention Weights)

上面的分数是原始数值（logits），我们需要把它们变成概率分布（总和为 1，且都为正数）。这通常使用 Softmax 函数来实现。

代码实现：

# 使用 softmax 进行归一化
# dim=0 表示沿着向量长度方向进行计算
attn_weights_2 = torch.softmax(attn_scores_2, dim=0)

print("注意力权重:", attn_weights_2)
print("权重总和:", attn_weights_2.sum())

执行结果：

注意力权重: 
tensor([0.1385, 0.2379, 0.2333, 0.1240, 0.1082, 0.1581])
权重总和: tensor(1.)

现在我们知道了，在计算 “journey” 的上下文时，应该分配 23.79% 的注意力给它自己，23.33% 给 “starts”，以此类推。

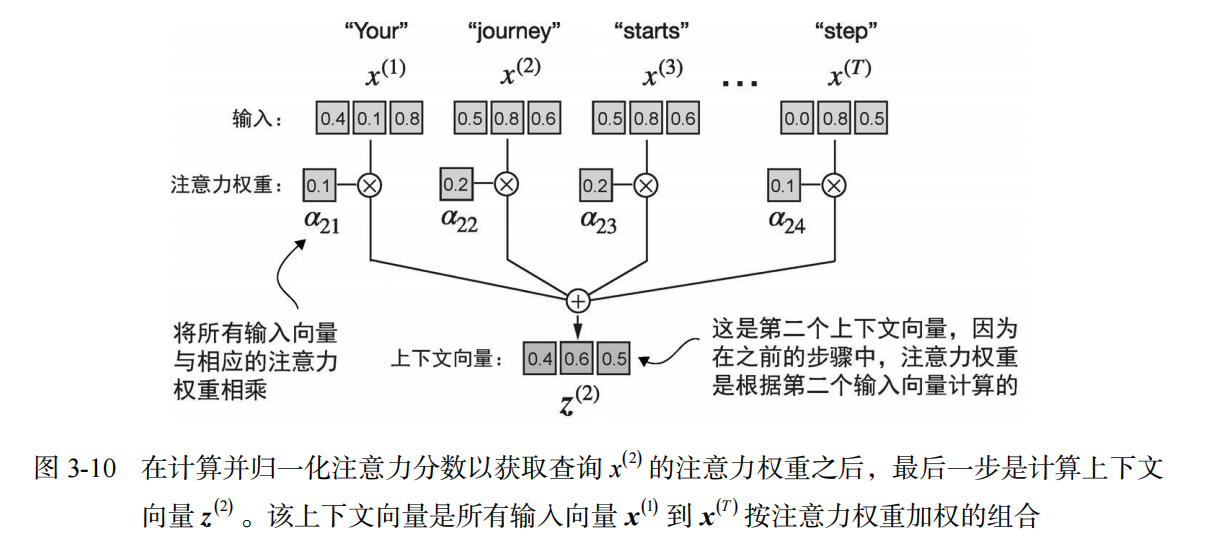
2.3 第三步：计算上下文向量 (Context Vector)

现在有了权重，后一步就是加权求和。把所有的输入向量 $x^{(i)}$ 乘以对应的权重 $\alpha_i$，然后加起来。

代码实现：

# 初始化上下文向量为全0
context_vec_2 = torch.zeros(query.shape)

# 遍历所有输入向量，进行加权累加
for i, x_i in enumerate(inputs):
    context_vec_2 += attn_weights_2[i] * x_i

print("上下文向量 z(2):", context_vec_2)

执行结果：

上下文向量 z(2): tensor([0.4419, 0.6515, 0.5683])

结论： 这个新的向量 [0.4419, 0.6515, 0.5683] 就是 “journey” 这个词在这个句子中的增强表示，它融合了整个句子的信息。

3. 进阶：向量化实现

写 for 循环太慢了。在深度学习中，我们总是利用矩阵乘法（Matrix Multiplication）来一次性处理所有数据。

3.1 计算所有对所有 (All-to-All) 的分数

我们可以通过 inputs 矩阵乘以它的转置 inputs.T，一步算出 6x6 的分数矩阵。

# 矩阵乘法：(6, 3) @ (3, 6) -> (6, 6)
# 这相当于计算了每对单词之间的点积
attn_scores = inputs @ inputs.T

print("所有注意力分数矩阵:\n", attn_scores)

执行结果：

所有注意力分数矩阵:
 tensor([[0.9995, 0.9544, 0.9422, 0.4753, 0.4576, 0.6310],
         [0.9544, 1.4950, 1.4754, 0.8434, 0.7070, 1.0865],
         [0.9422, 1.4754, 1.4570, 0.8296, 0.7154, 1.0605],
         [0.4753, 0.8434, 0.8296, 0.4937, 0.3474, 0.6565],
         [0.4576, 0.7070, 0.7154, 0.3474, 0.6654, 0.2935],
         [0.6310, 1.0865, 1.0605, 0.6565, 0.2935, 0.9450]])

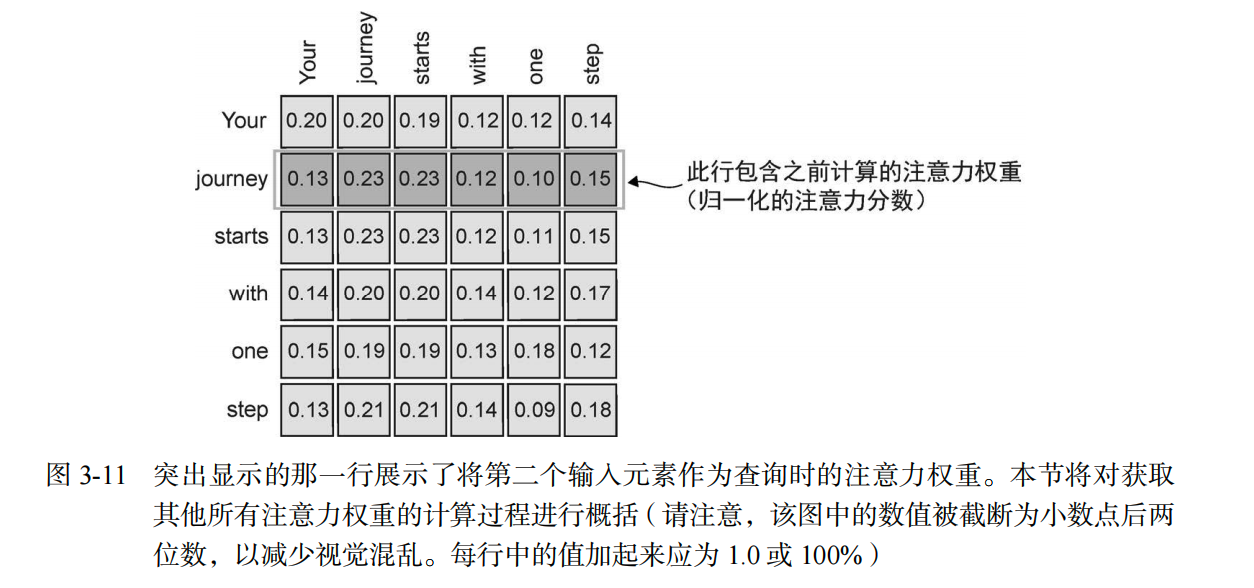
第 2 行的数据 [0.9544, 1.4950 ...] 和我们在 2.1 节里算的一模一样。

3.2 归一化权重

对矩阵的每一行进行 Softmax。

# dim=-1 表示对每一行（后一个维度）进行归一化
attn_weights = torch.softmax(attn_scores, dim=-1)

print("所有注意力权重矩阵:\n", attn_weights)

执行结果：

所有注意力权重矩阵:
 tensor([[0.2098, 0.2006, 0.1981, 0.1242, 0.1220, 0.1452],
         [0.1385, 0.2379, 0.2333, 0.1240, 0.1082, 0.1581],
         ... (省略中间行) ...
         [0.1385, 0.2184, 0.2128, 0.1420, 0.0988, 0.1896]])

3.3 计算所有上下文向量

后一步，矩阵乘法再次登场。用权重矩阵乘以输入矩阵。

# (6, 6) @ (6, 3) -> (6, 3)
all_context_vecs = attn_weights @ inputs

print("所有上下文向量:\n", all_context_vecs)

执行结果：

所有上下文向量:
 tensor([[0.4421, 0.5931, 0.5790],
         [0.4419, 0.6515, 0.5683],  <-- 这一行和我们在 2.3 节算的一样
         [0.4431, 0.6496, 0.5671],
         [0.4304, 0.6298, 0.5510],
         [0.4671, 0.5910, 0.5266],
         [0.4177, 0.6503, 0.5645]])

4. 总结：这节课学了什么？

这节展示了 “简化版” 的自注意力机制。它没有需要学习的参数（那是下一节 3.4 的内容，会引入 $W_q, W_k, W_v$ 权重矩阵）。

核心逻辑图 (ASCII Art):

[ 输入矩阵 X ]  (6行3列)
      |
      |  1. 点积 (X 乘以 X的转置)
      v
[ 分数矩阵 ]    (6行6列，表示相关性)
      |
      |  2. Softmax (归一化)
      v
[ 权重矩阵 ]    (6行6列，概率分布)
      |
      |  3. 加权和 (权重矩阵 乘以 输入矩阵 X)
      v
[ 上下文矩阵 Z ] (6行3列，增强后的表示)

关键点：

1. 全局视野： 每个单词的更新都利用了整个句子的信息。
2. 无需循环： 使用矩阵乘法可以并行计算所有位置，这对 GPU 来说非常高效。
3. 相似度驱动： 注意力机制本质上是在问：“对于当前单词，其他单词有多重要？”

这就是自注意力机制的“心脏”。下一节，我们将给这个心脏加上“阀门”（可训练的权重矩阵），让它能够学习应该关注什么，而不是简单地计算几何相似度。