二叉堆与优先级队列的关系

目录

• 1. 二叉堆的概念
  • 1.1. 二叉堆的存储示意图
  • 1.2. 以小顶堆为例
• 2. 二叉堆与优先级队列的关系
• 3. 总结

1. 二叉堆的概念

二叉堆在逻辑上其实是一种特殊的二叉树（完全二叉树），只不过存储在数组里。

• 一般的链表二叉树，我们操作节点的指针
• 而在数组里，我们把数组索引作为指针

即：链式存储-链表 和 顺序存储-数组 ，如下

1.1. 二叉堆的存储示意图

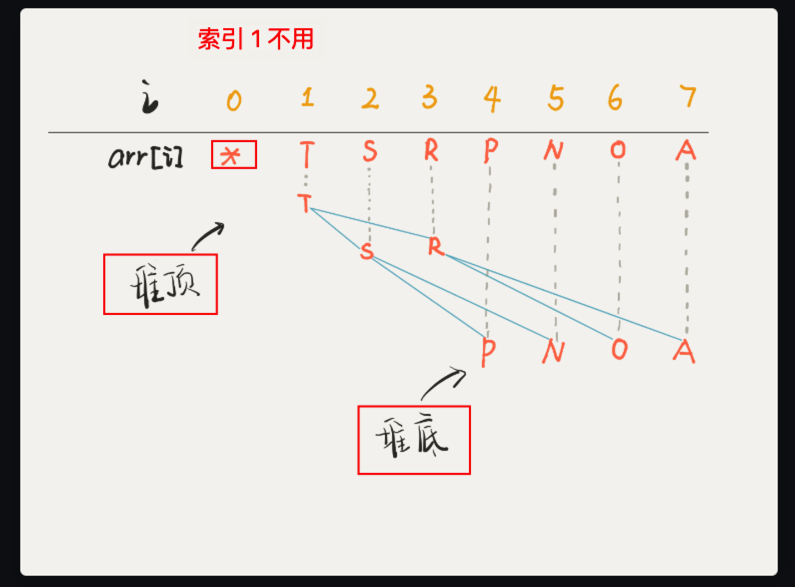
1.2. 以小顶堆为例

1、这种二叉树数据结构通过 数组 的方式存储 2、需要维护每个节点的关系，即大于或者小于它的两个子节点，所以有上浮和下沉 两个操作 3、关于循环，使用 while 或者 递归，比如一直下沉到具体什么条件，即递归。

2. 二叉堆与优先级队列的关系

优先级队列这种数据结构，在插入或者删除元素的时候，元素会自动排序，这底层的原理就是二叉堆的操作，==就是这关系而已。==

但真正在一些算法题里，不可能单独还在实现一个二叉堆的数据结构，所以往往只是实现部分逻辑，甚至都不采用这种堆数据结构，完全独立实现。如 合并 K 个有序链表 中的 优先级入队函数，其实和二叉堆没有什么区别。

// 优先级队列，值最小的先入队，即优先级最高
let q = [];
// 优先队列的【入队函数】，值最小的先入队列
let enqueue = (node) => {
	if (q.length === 0) {
		q.push(node);
	} else {
		// 是否插入了
		let added = false;
		for (let i = 0; i < q.length; i++) {
			if (node.val < q[i].val) {
				q.splice(i, 0, node)
				added = true;
				break;
			}
		}
		// 没找到合适的插入位置，则添加到末尾
		if (!added) {
			q.push(node);
		}
	}
}

当然，还是因为 JavaScript 没有对应的公共数据结构库，Leetcode 专门提供了专门的库，记得使用，别自己实现。对应 Java 就有 PriorityQueue

3. 总结

• 二叉堆就是一种 完全二叉树，所以适合存储在数组中，而且二叉堆拥有一些特殊性质。
• 二叉堆的操作很简单，主要就是 上浮和下沉，来维护堆的性质（堆有序）
• 优先级队列是基于二叉堆实现的，主要操作是插入和删除。
  • 插入是先插到最后，然后上浮到正确位置
  • 删除是 调换位置后再删除，然后下沉到正确位置