重新规划路线

#leetcode #算法 #DFS #算法/图

目录

题目及理解

https://leetcode.cn/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero/description/?envType=study-plan-v2&envId=leetcode-75

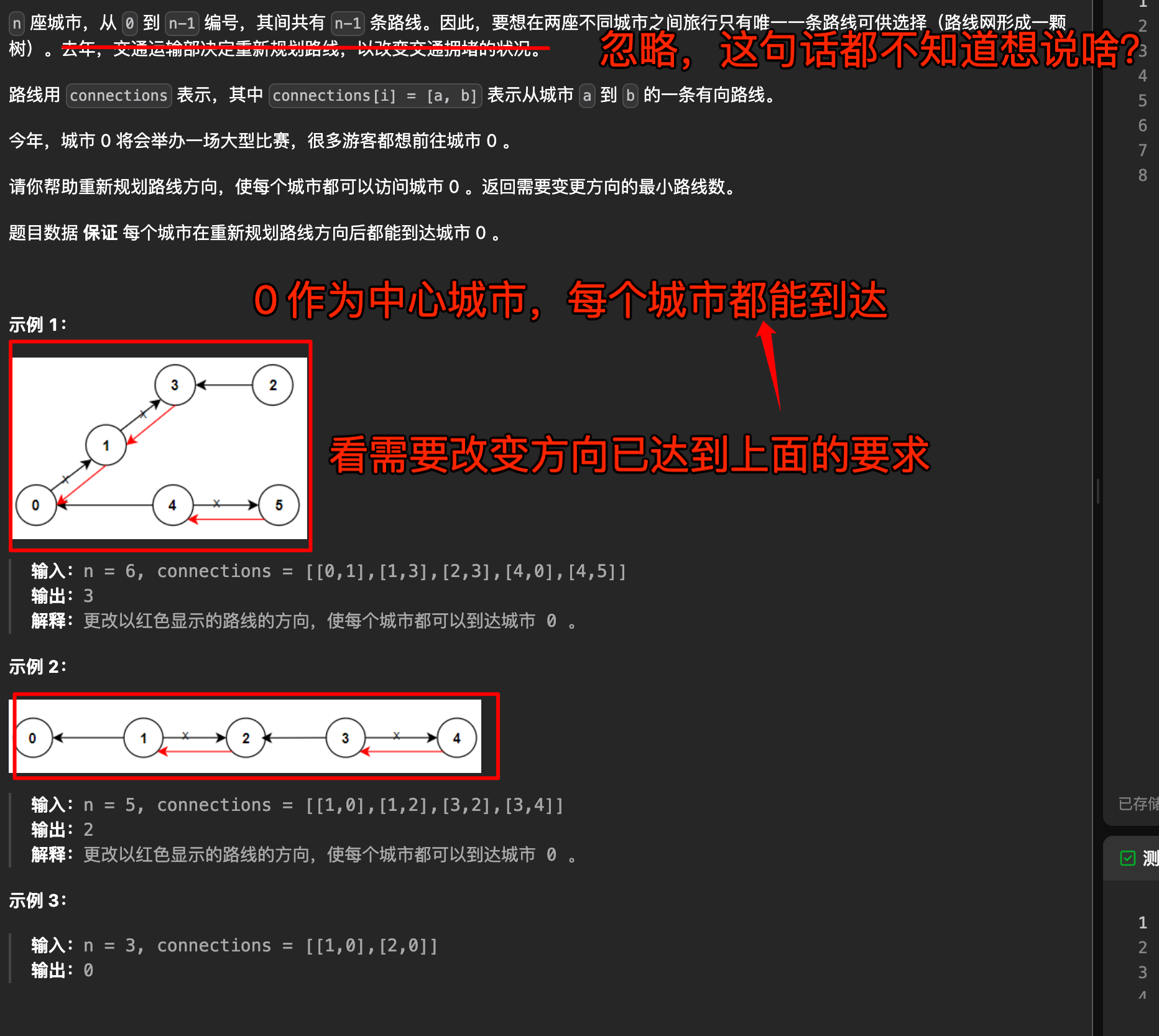
cos-blog-832-34-20241012|600

思路

  1. 建图：
    • 首先，将给定的有向边数组转换为一个无向图（邻接表）
    • 同时，使用一个集合来记录原有的有向边，以便在之后判断是否需要反转边的方向
  2. 深度优先搜索（DFS）
    • 从节点 0 开始进行 DFS 遍历，对于每个未访问过的相邻节点
      • 如果通过当前节点到达相邻节点的边是原有的有向边，则需要增加一次反转计数。
      • 继续递归遍历相邻节点
  3. 统计反转次数：在 DFS 的过程中，统计需要反转的边的数量。

题设中是要求，每个城市都能到到达 城市 0 ，所以从 0 开始深度遍历，遍历过程中，如果不包含原始有向边，则将计数器 + 1

代码实现

/**
 * @param {number} n
 * @param {number[][]} connections
 * @return {number}
 */
var minReorder = function (n, connections) {
  // 构建邻接表
  const graph = new Array(n).fill(0).map(() => []);
  // 记录原始边，使用 Set 避免重复，key 为 "u,v"，表示 u 到 v 的有向边
  const originalEdges = new Set();

  // 使用有向边构建邻接表（无向）
  for (const [u, v] of connections) {
    graph[u].push(v);
    graph[v].push(u);
    originalEdges.add(`${u},${v}`);
  }

  // 记录反向边的数量(需要重新规划的边的数量)
  let reorderCount = 0;
  // 记录节点是否被访问
  const visited = new Array(n).fill(false);

  function dfs(node) {
    visited[node] = true;
    for (const neighbor of graph[node]) {
      if (!visited[neighbor]) {
        // 检查是否需要反转
        // 如果原始边集合中有 neighbor 到 node 的边,则不需要反转，即能够达到中心城市 0
        // 否则，需要反转
        // 即如下代码，node 到 neighbor 的边需要反转，node 代表中心城市 0
        if (originalEdges.has(`${node},${neighbor}`)) {
          reorderCount++;
        }
        dfs(neighbor);
      }
    }
  }

  // 从节点 0 开始 DFS
  dfs(0);
  return reorderCount;
};

复杂度分析

时间复杂度：O(N + E)

  • N 是城市的数量，E 是连接的数量。
  • 构建邻接表和原始边集合需要 O(E) 的时间。
  • DFS 遍历每个节点和边一次，总共需要 O(N + E) 的时间。
  • 对于每个边，检查是否需要反转的操作（使用 Set 的 has 方法）是 O(1) 的。

空间复杂度：O(N + E)

  • 邻接表 graph 需要 O(N + E) 的空间。
  • 原始边集合 originalEdges 需要 O(E) 的空间。
  • visited 数组需要 O(N) 的空间。
  • 递归调用栈在最坏情况下可能达到 O(N) 的深度。

总结：

  • 时间复杂度：O(N + E)
  • 空间复杂度：O(N + E)

这个算法的效率相当高，因为它只需要遍历每个节点和边一次。使用 Set 来存储原始边可以在 O(1) 时间内检查边的方向，这是一个很好的优化。整体来说，这是一个高效的解决方案，适用于大规模的输入数据。