从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

• 后序遍历的

• base case

  • inStart > inEnd 和 postStart > postEnd 是等价的

• 需要计算当前左子树的节点数量

  • leftSize = inRootIndex - inStart

• 构建左右子树：

  • 
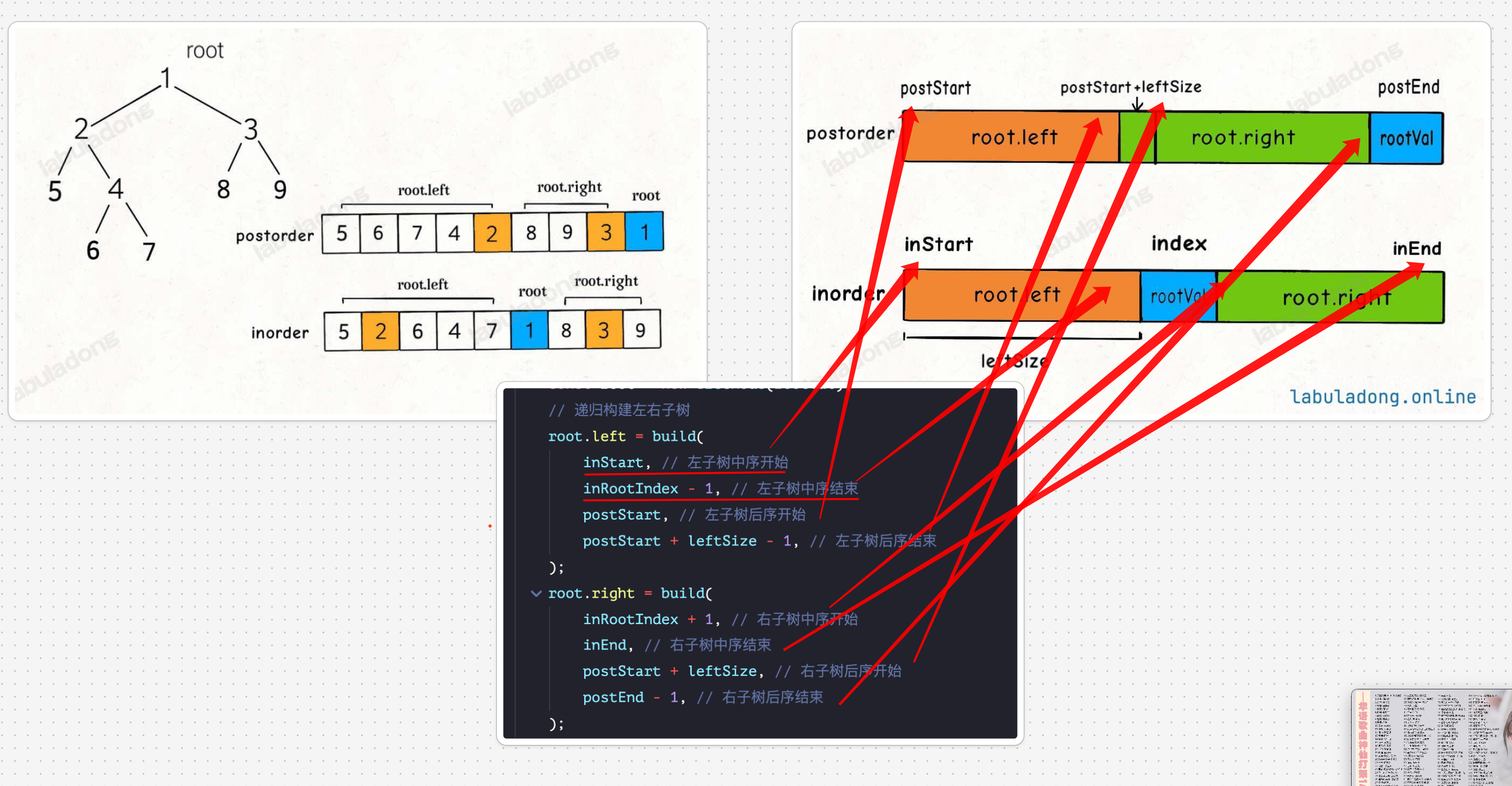
  • 找到左子树的
    • 中序开始
    • 中序结束
    • 后序开始
    • 后序结束
  • 找到后子树的
    • 中序开始
    • 中序结束
    • 后序开始
    • 后序结束

var buildTree = function (inorder, postorder) {
    // 创建中序遍历的值到索引的映射，方便快速查找
    const map = new Map();
    inorder.forEach((val, index) => {
        map.set(val, index);
    });

    function build(inStart, inEnd, postStart, postEnd) {
        if (inStart > inEnd) return null;
        // if (postStart > postEnd) return null;
        // 后序遍历的最后一个节点是根节点
        const rootVal = postorder[postEnd];

        // 在中序遍历中找到根节点位置
        const inRootIndex = map.get(rootVal);
        // 计算左子树的节点数量
        const leftSize = inRootIndex - inStart;

        const root = new TreeNode(rootVal);
        // 递归构建左右子树
        root.left = build(
            inStart, // 左子树中序开始
            inRootIndex - 1, // 左子树中序结束
            postStart, // 左子树后序开始
            postStart + leftSize - 1, // 左子树后序结束
        );
        root.right = build(
            inRootIndex + 1, // 右子树中序开始
            inEnd, // 右子树中序结束
            postStart + leftSize, // 右子树后序开始
            postEnd - 1, // 右子树后序结束
        );

        return root;
    }

    return build(0, inorder.length - 1, 0, postorder.length - 1);
};