树的一些基本概念

#算法/二叉树 #算法/树 #算法/数据结构 #2023/04/18

1. 二叉树、满二叉树、完全二叉树
2. 堆、大顶堆、小顶堆
3. 疑问：数据结构中的堆栈 与内存中的堆栈 的区别？
4. 查找二叉树（二叉搜索树）
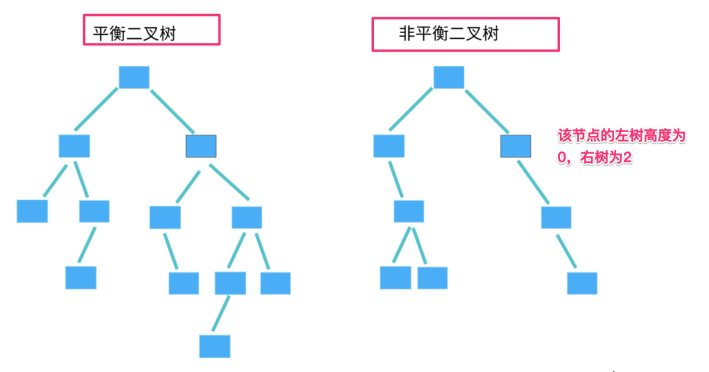
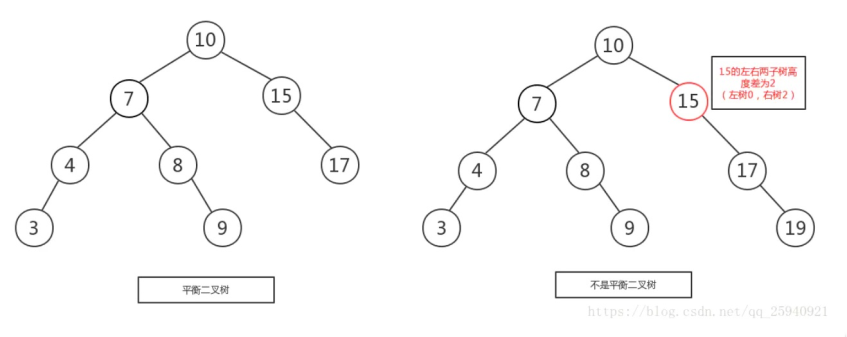
5. 平衡二叉查找树
6. 二叉树的存储方式
- 6.1. 链式存储 - 对象
- 6.2. 顺序存储 - 数组
7. 数据结构设计 - 实现一个二叉搜索树

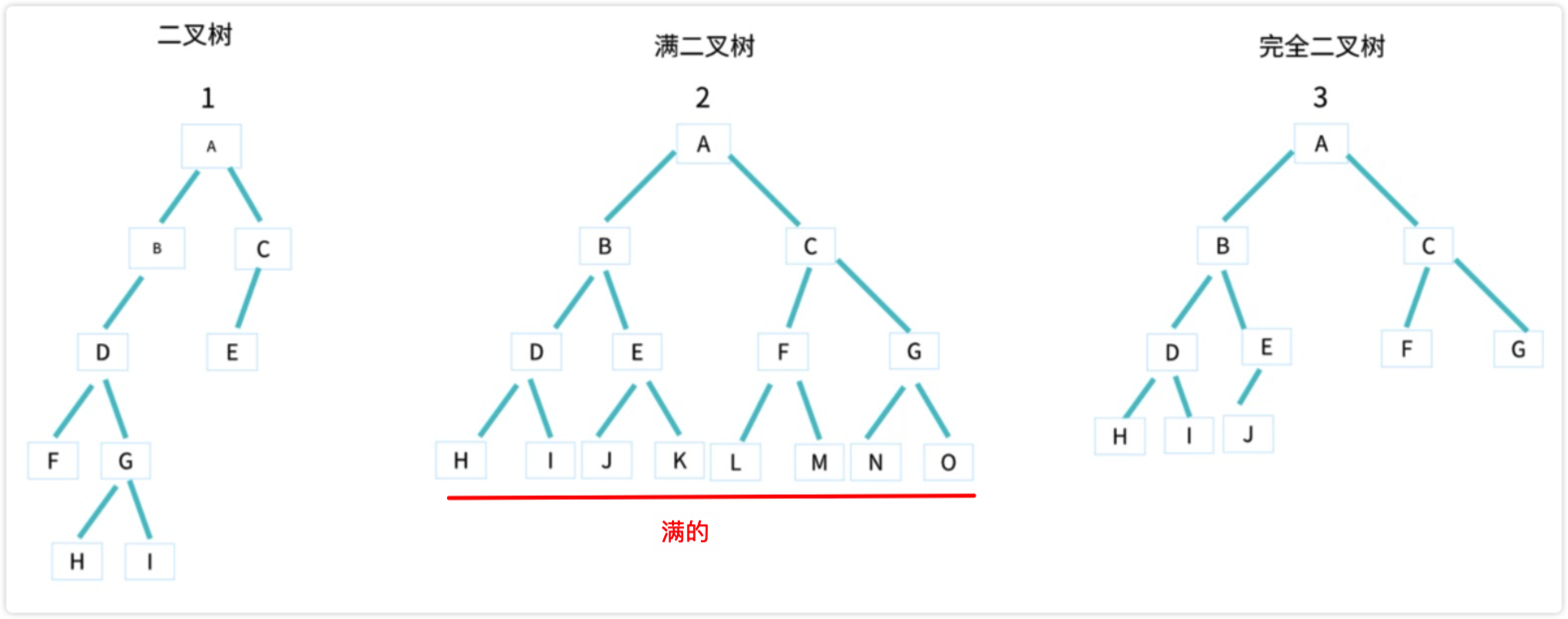
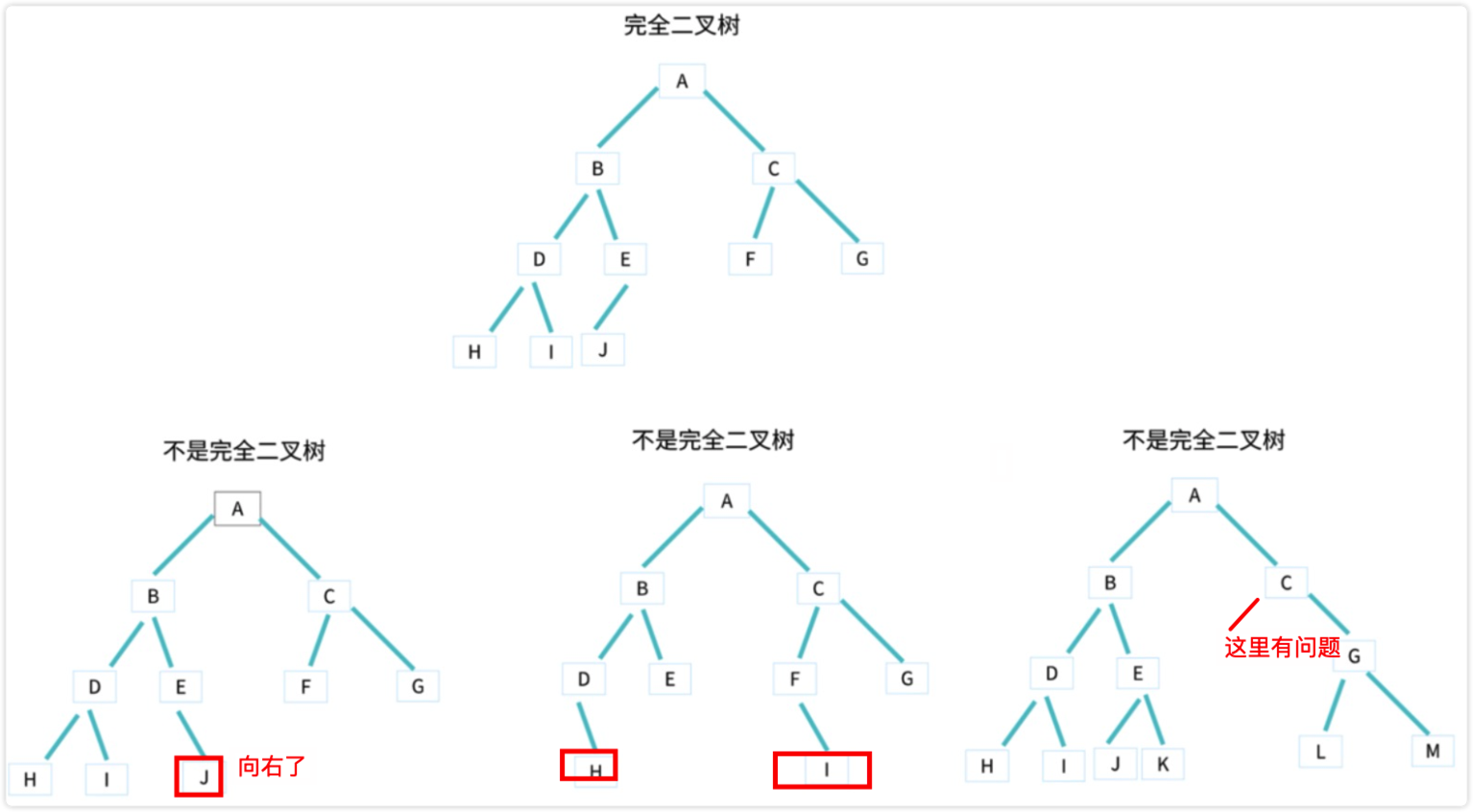
1. 二叉树、满二叉树、完全二叉树

这里着重说下完全二叉树：

叶子节点都在 最底下两层
最后一层叶子节都靠左排列
并且除了最后一层，其他层的节点个数都要达到最大

|592 |568

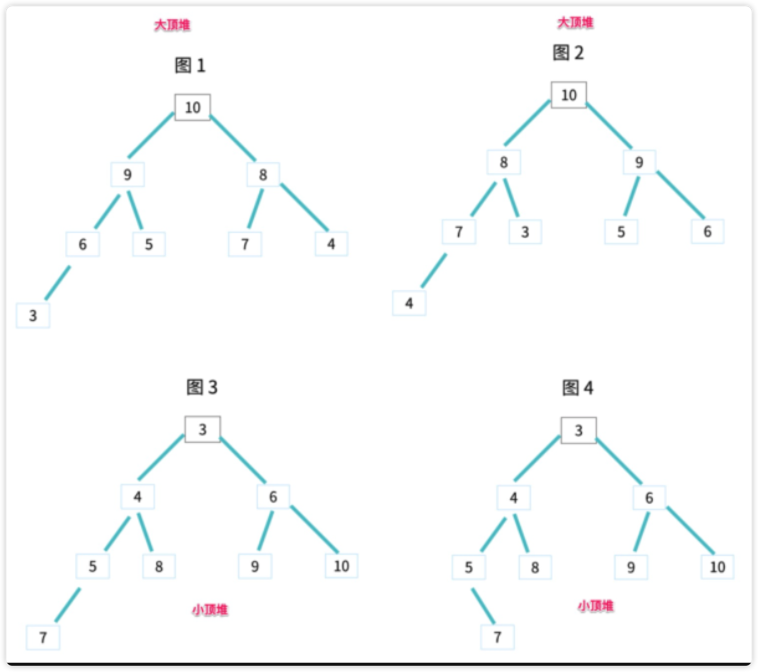
2. 堆、大顶堆、小顶堆

2.1. 堆的基本概念

堆是一个完全二叉树。
堆中 每个节点的值都 大于等于（或者小于等于）其左右子节点的值
- 大的再上面，大顶堆
- 小的再上面，小顶堆

2.2. 堆的价值

2.2.1. 大顶堆的价值

优先队列
高效排序
高效的动态中位数

2.2.2. 小顶堆的价值

主要价值和应用：

优先队列：小顶堆也常用于实现优先队列，支持快速获取和删除最小元素。
图算法：在图算法中，小顶堆用于实现 Dijkstra 最短路径算法和 Prim 最小生成树算法，以快速找到权重最小的边或路径。
合并有序列表：小顶堆可以高效地合并多个有序列表，例如用于外部排序或归并排序

2.2.2.1. 堆的总体价值

高效的插入和删除操作：堆支持 O(log n) 的插入和删除操作，使其在需要频繁调整元素顺序的场景中非常高效。
内存利用率高：堆是一种基于数组实现的数据结构，内存利用率高，不需要额外的指针或链接。
广泛应用：堆在各种算法和系统中有广泛应用，包括调度系统、内存管理、图算法、实时数据处理等。

总之，堆结构因其高效的插入、删除和查找操作，在许多需要维护动态有序集合的场景中具有重要价值。

2.3. 实现一个`小顶堆`

使用数组来存储，代码如下：

关键是 this.head = [] 来存储

function swap(array, a, b) {
    [array[a], array[b]] = [array[b], array[a]];
}

class MinHeap {
    constructor() {
        // 使用数组来存储
        this.heap = [];
    }

    // 左孩子的索引
    getLeftIndex(index) {
        return (2 * index) + 1;
    }

    // 右孩子的索引
    getRightIndex(index) {
        return (2 * index) + 2;
    }

    // 父节点的索引
    getParentIndex(index) {
        if (index === 0) {
            return 0;
        }
        return Math.floor((index - 1) / 2);
    }

    // 返回个数
    size() {
        return this.heap.length;
    }

    isEmpty() {
        return this.size() <= 0;
    }

    clear() {
        this.heap = [];
    }
    // ::::小顶堆，最小的肯定在最上面
    findMinimum() {
        return this.isEmpty() ? null : this.heap[0];
    }

    // 插入一个值，插入的元素添加到堆底的最后，然后让其上浮到正确位置（如果大顶的话）
    insert(value) {
        if (value != null) {
            const index = this.heap.length;
            // 先放在最后一位
            this.heap.push(value);
            // 父节点向上移动，直到父节点小于插入的值
            this.siftUp(index);
            return true;
        }
        return false;
    }

    // 下沉，堆化，递归
    siftDown(index) {
        // 插入的元素的位置
        let element = index;
        const left = this.getLeftIndex(index);
        const right = this.getRightIndex(index);
        const size = this.size();

        if (left < size  // base 判断
            && this.heap[element] > this.heap[left] 
            // 如果该元素大于它的左子节点，则下沉
        ) {
            element = left;
        }

        if (right < size // base判断
            && this.heap[element] > this.heap[left]  
            // 如果该元素大于它的右子节点，则下沉
        ) {
            element = right;
        }

        // 如果element 最后 和传入的index不一样了，说明需要交换数据，然后继续下沉递归
        if (index !== element) {
            swap(this.heap, index, element);
            this.siftDown(element);
        }

    }

    // 向上移动，直到父节点的值小于插入的值
    siftUp(index) {
        let parent = this.getParentIndex(index);
        while (
            index > 0 // base 判断
            && this.heap[parent] > this.heap[index]) // 父节点的元素大于子元素的时候，才需要移动
        {
            swap(this.heap, parent, index);
            index = parent;
            parent = this.getParentIndex(index);
        }
    }

    // delete min 堆顶元素（最小值）和 堆底元素 对调
    // 1、删除删除堆顶元素
    // 2、让堆底元素沉到正确位置
    deleteMin() {
        if (this.isEmpty()) {
            return null;
        }
        if (this.size() === 1) {
            return this.heap.shift();
        }
        const removedValue = this.heap[0]; // 堆顶元素
        const lastElement = this.heap.pop();  // 移除堆底元素
        this.heap[0] = lastElement; // 将 堆顶元素 赋值为 堆底元素
        // 从堆顶开始下沉
        this.siftDown(0);
        return removedValue;
    }

    getAsArray() {
        return this.heap;
    }
}

let arr = [5, 3, 7, 9, 0, 0, -1, -2, 7, -8];

let heapObj = new MinHeap();
arr.forEach((item) => {
    heapObj.insert(item)
})
console.log(heapObj);
console.log('************************')

console.log(heapObj.findMinimum());

// MinHeap { heap: [
//     -8, -2, 0, 3, -1,
//      7,  0, 9, 7,  5
//   ] }
// ************************
// -8

3. 疑问：数据结构中的`堆栈` 与内存中的`堆栈` 的区别？

|568 |568

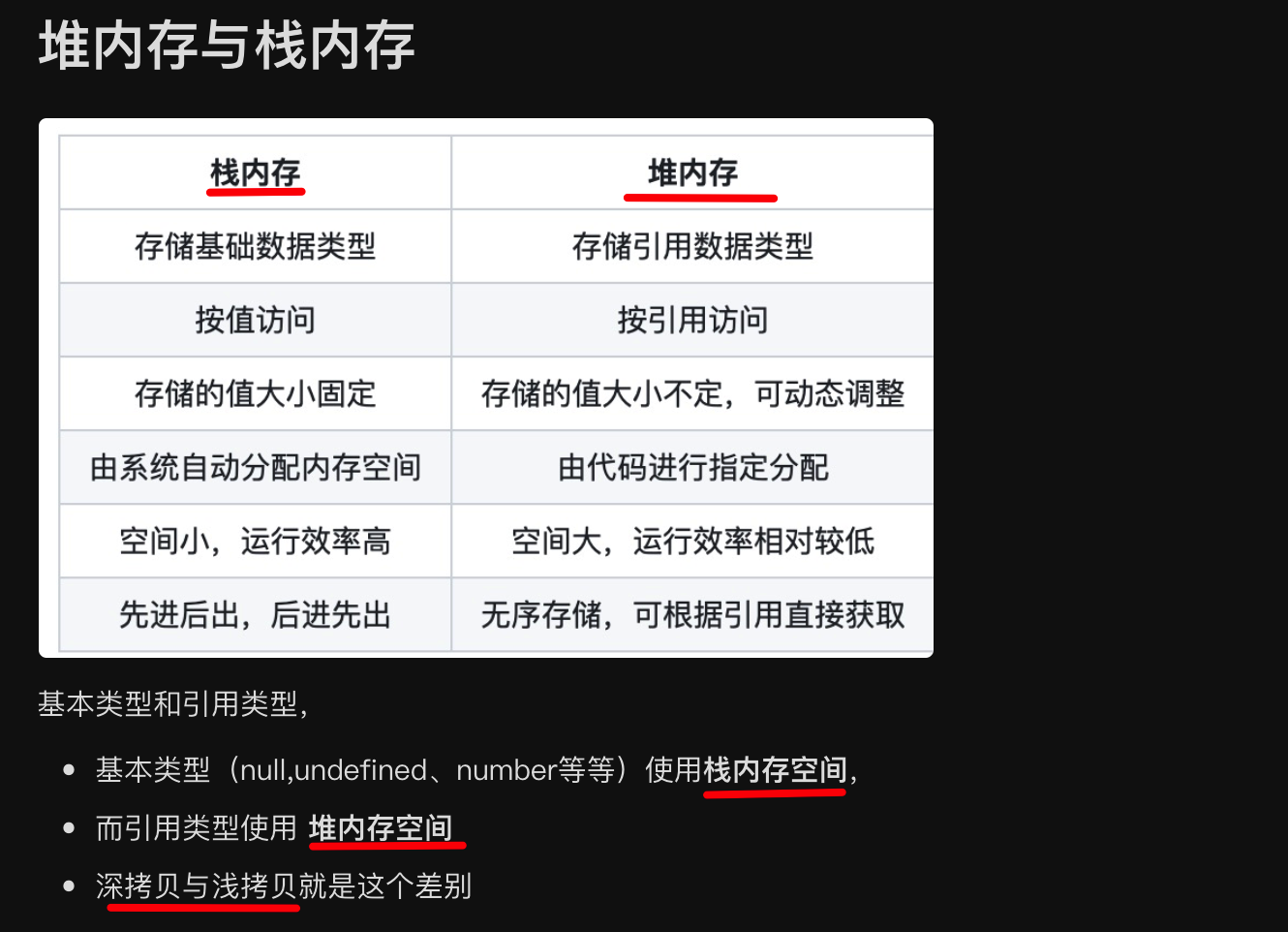
堆内存（Heap Memory）和栈内存（Stack Memory）是计算机内存管理中两种不同的内存分配区域。它们在用途、管理方式、生命周期和性能上有显著区别。以下是它们的主要区别：

3.1. 用途

堆内存
- 用于动态分配内存，通常由程序运行时分配和释放。
- 适用于需要在运行时决定大小和生命周期的对象和数据结构，例如动态数组、链表等。
栈内存
- 用于静态分配内存，主要用于函数调用、局部变量和函数参数。
- 适用于生命周期明确且较短的变量，例如局部变量和函数参数。

3.2. 管理方式

堆内存：
- 内存管理较复杂，容易导致内存泄漏和碎片化问题。
- 由程序员显式分配（如 malloc 在 C/C++ 中，new 在 C++/Java 中）和释放（如 free 在 C/C++ 中，垃圾回收在 Java 中）。
栈内存：
- 内存管理简单，不会出现内存泄漏问题，但栈空间有限，不能用于大对象或长生命周期对象。
- 由编译器自动管理，内存分配和释放在函数调用和返回时自动进行。

3.3. 生命周期

堆内存：
- 对象的生命周期由程序员控制，可以在程序运行过程中动态分配和释放。
- 对象在不再使用后需要显式释放，否则会导致内存泄漏。
栈内存
- 对象的生命周期由函数调用栈决定，当函数返回时，栈上的所有局部变量自动销毁。
- 生命周期短暂且明确，不需要显式释放。

3.4. 性能

堆内存：
- 动态分配和释放内存的开销较大，因为需要查找合适的内存块，并处理碎片化问题。
- 常见于需要灵活管理内存的大型复杂应用中。
栈内存：
- 更适合小型、短生命周期的数据，具有更高的访问速度。
- 内存分配和释放速度快，仅通过移动栈指针即可完成。

3.5. 总结

堆内存：适用于动态分配的对象，生命周期由程序员控制，管理复杂但灵活。
栈内存：适用于局部变量和函数调用，生命周期短暂且由编译器自动管理，性能高但空间有限。

理解堆和栈的区别对于高效编写和调试代码至关重要，尤其是涉及到内存管理和性能优化时。

4. 查找二叉树（二叉搜索树）

一种特殊的二叉树，较小的值保存在左节点中，较大的值保存在右节点中
- 根节点的左子树都比根节点的值小，右子树的值都比根节点的值大。
- 二叉查找树是一种有序的树，所以支持快速查找、快速插入、删除一个数据

|576

5. 平衡二叉查找树

二叉树中任意一个节点的左右子树的高度相差不能大于 1 |560 |552

6. 二叉树的存储方式

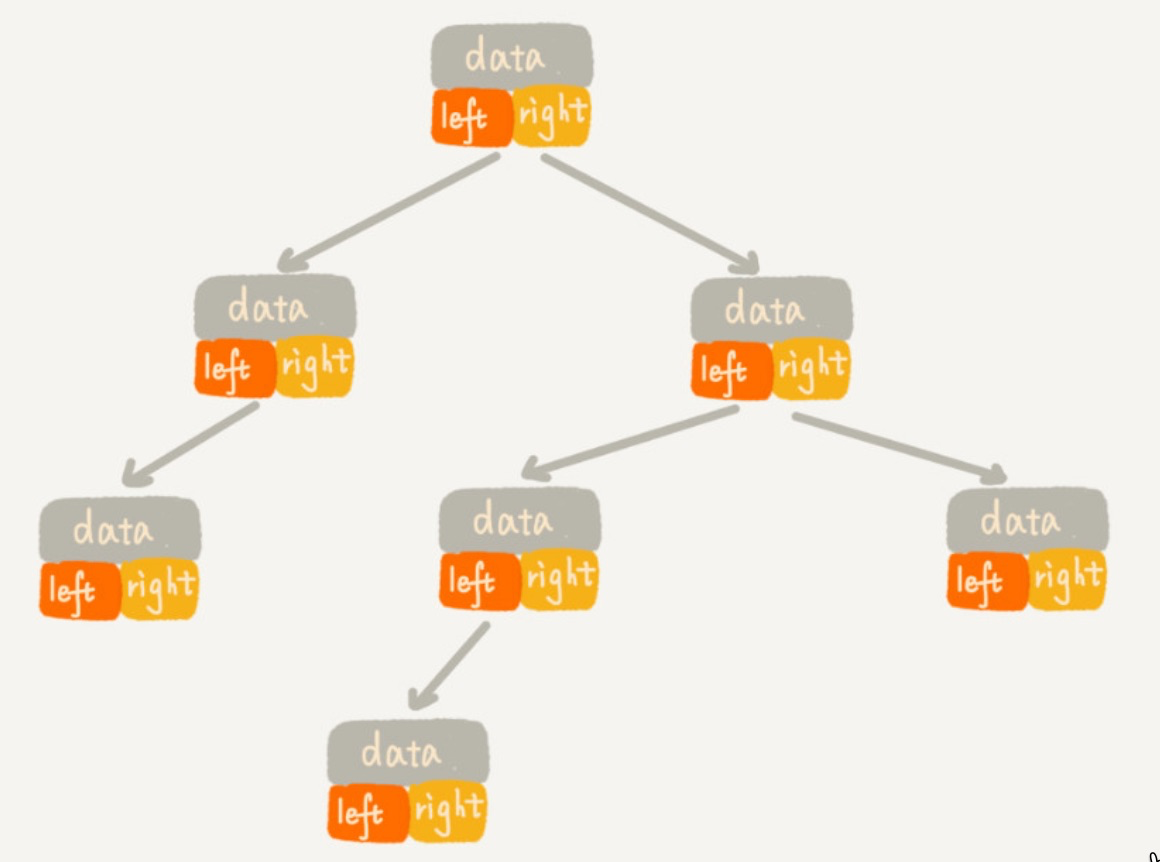
6.1. 链式存储 - 对象

|560

6.2. 顺序存储 - 数组

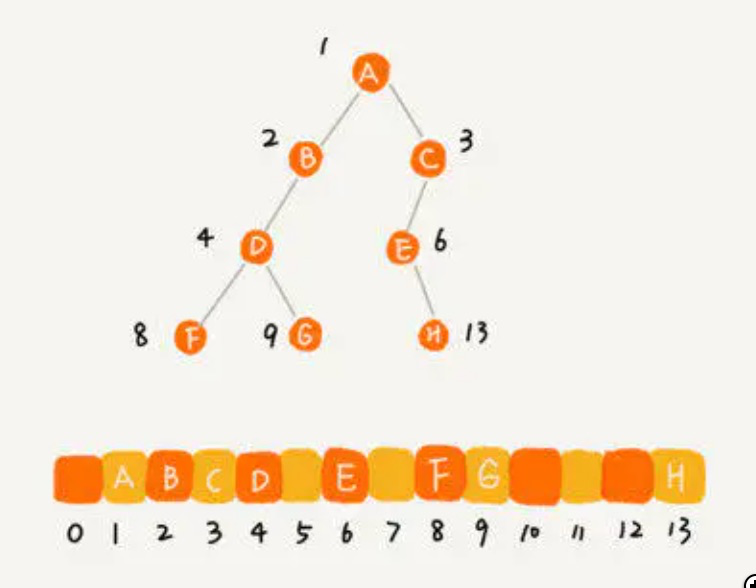
完全二叉树用数组来存储是最省内存的方式 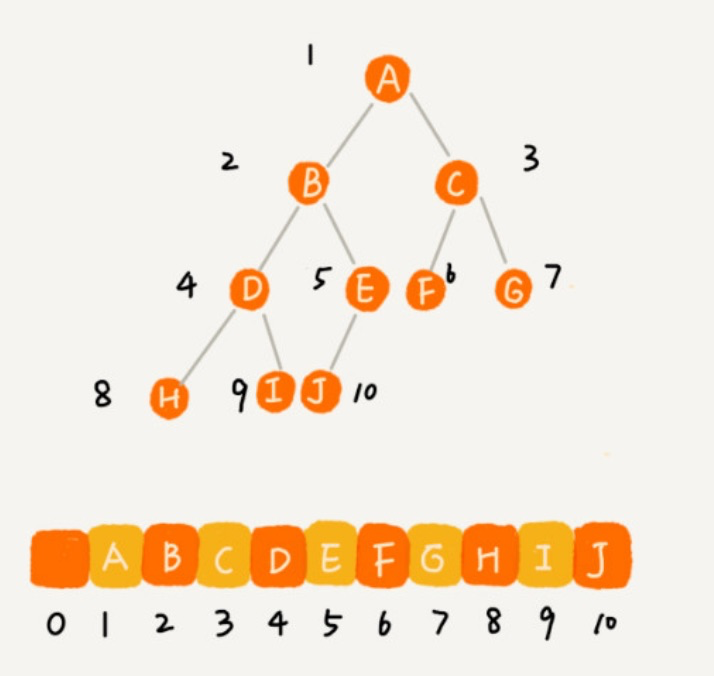|568 非完全二叉树则会浪费空间，如下图： |560

7. 数据结构设计 - 实现一个`二叉搜索树`

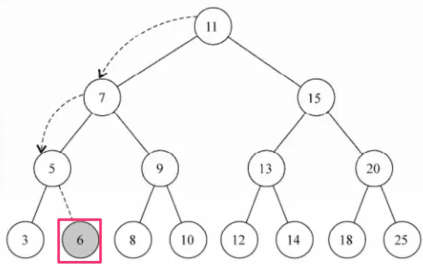
7.1. 插入节点

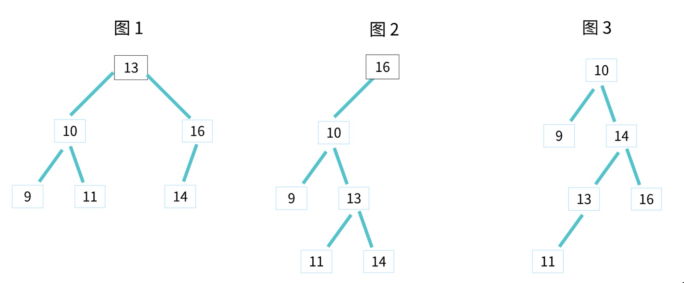
看下面一张图，在下图的树中插入健值为 6 的节点，过程如下： |391

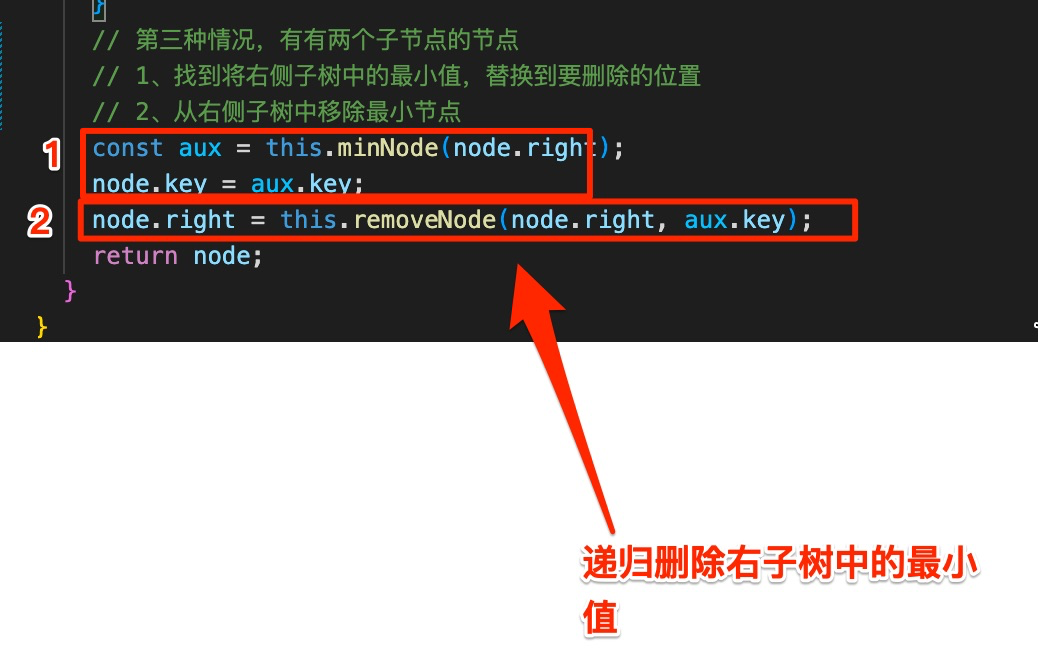
7.2. 移除节点

关键看下删除有两个子节点的节点： 1、【该节点与右子树中最小值位置置换】找到将右侧子树中的最小值，替换到要删除的位置 2、然后递归从从右侧子树中移除最小节点如下图： |495 |568

7.3. 代码部分

// node节点类
class Node {
    constructor(key) {
        this.key = key;
        this.left = null;
        this.right = null;
    }
    toString() {
        return `${this.key}`;
    }
}

export default class BinarySearchTree {

    constructor() {
        this.root = null;
    }

    // 向树中插入一个新的键。
    insert(key) {
        // special case: first key
        if (this.root == null) {
            this.root = new Node(key);
        } else {
            // 从root开始遍历查找合适的位置插入
            this.insertNode(this.root, key);
        }
    }

    // 遍历树，将插入节点的键值与遍历到的节点键值比较，如果前者大于后者，继续递归遍历右子节点，
    // 反之，继续遍历左子节点，直到找到一个空的节点，在该位置插入。
    insertNode(node, key) {
        // 如果插入节点的键值小于当前节点的键值，则需要插入左边
        if (key < node.key) {
            // 左节点没有值，则直接插入
            if (node.left == null) {
                node.left = new Node(key);
            } else {
                this.insertNode(node.left, key);
            }
            // 否则需要插入右边
        } else {
            if (node.right == null) {
                node.right = new Node(key);
            } else {
                this.insertNode(node.right, key);
            }
        }
    }
    getRoot() {
        return this.root;
    }
    inOrderTraverse(callback) {
        this.inOrderTraverseNode(this.root, callback);
    }
    inOrderTraverseNode(node, callback) {
        if (node != null) {
            this.inOrderTraverseNode(node.left, callback);
            callback(node.key);
            this.inOrderTraverseNode(node.right, callback);
        }
    }

    preOrderTraverse(callback) {
        this.preOrderTraverseNode(this.root, callback);
    }

    preOrderTraverseNode(node, callback) {
        if (node != null) {
            callback(node.key);
            this.preOrderTraverseNode(node.left, callback);
            this.preOrderTraverseNode(node.right, callback);
        }
    }

    postOrderTraverse(callback) {
        this.postOrderTraverseNode(this.root, callback);
    }

    postOrderTraverseNode(node, callback) {
        if (node != null) {
            this.postOrderTraverseNode(node.left, callback);
            this.postOrderTraverseNode(node.right, callback);
            callback(node.key);
        }
    }

    search(key) {
        return this.searchNode(this.root, key);
    }

    // 搜索特定值的处理与插入值的处理类似。遍历树，
    // 将要搜索的值与遍历到的节点比较，如果前者大于后者，
    // 则递归遍历右侧子节点，反之，则递归遍历左侧子节点。
    searchNode(node, key) {
        if (node == null) {
            return false;
        }
        // 如果要查找的值小于该节点，继续递归遍历其左侧节点
        if (key < node.key) {
            return this.searchNode(node.left, key);
        }
        // 如果要查找的值大于该节点，继续递归遍历其右侧节点
        if (key > node.key) {
            return this.searchNode(node.right, key);
        }
        return true;
    }

    min() {
        return this.minNode(this.root);
    }

    // 在二叉搜索树里，不管是整个树还是其子树，最小值一定在树最左侧的最底层。
    // 因此给定一颗树或其子树，只需要一直向左节点遍历到底就行了。
    minNode(node) {
        let current = node;
        while (current != null && current.left != null) {
            current = current.left;
        }
        return current;
    }

    max() {
        return this.maxNode(this.root);
    }

    // 搜索最大值与搜索最小值类似，只是沿着树的右侧遍历。
    maxNode(node) {
        let current = node;
        while (current != null && current.right != null) {
            current = current.right;
        }
        return current;
    }

    // 移除节点，首先要在树中查找到要移除的节点，再判断该节点是否有子节点、有一个子节点或者有两个子节点，最后分别处理。
    remove(key) {
        // 同样从root开始遍历查找
        this.root = this.removeNode(this.root, key);
    }

    removeNode(node, key) {
        // 如果 node 不存在，直接返回
        if (node == null) {
            return null;
        }
        // 找到要删除的node
        node = this.searchNode(node, key)

        // 第一种情况，该节点没有子节点
        if (node.left == null && node.right == null) {
            node = null;
            return node;
        }
        // 第二种情况，该节点只有一个子节点的节点
        if (node.left == null) {
            // 将右子节点替换自己
            node = node.right;
            return node;
        }
        if (node.right == null) {
            // 将左子节点替换自己
            node = node.left;
            return node;
        }
        // 第三种情况，有有两个子节点的节点
        // 1、找到将右侧子树中的最小值，替换到要删除的位置
        // 2、从右侧子树中移除最小节点
        const aux = this.minNode(node.right);
        node.key = aux.key;
        node.right = this.removeNode(node.right, aux.key);
        return node;
    }
}

liguwe's site