以图判树：判断图是否可以生成树

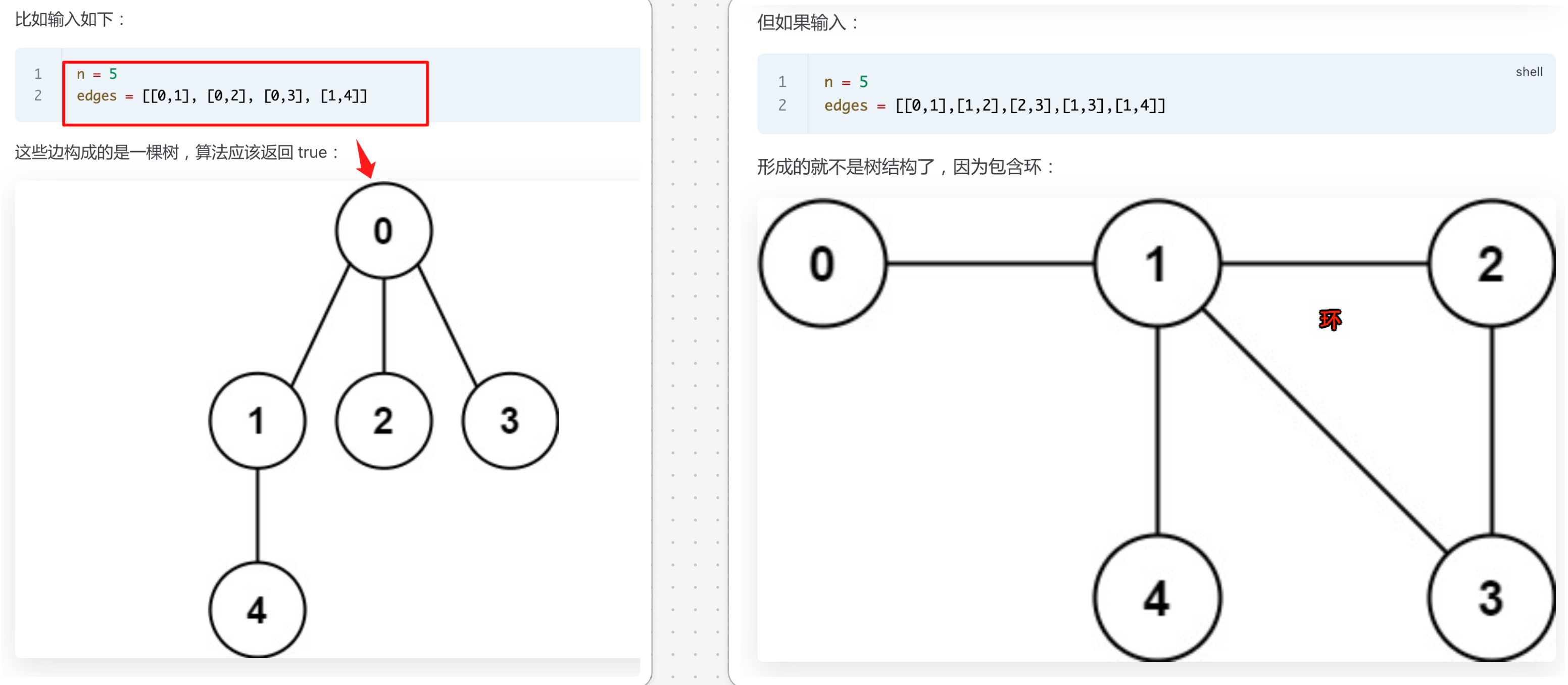
261. 以图判树

目录

• 1. 题目
• 2. 分析：每添加一条边
• 3. 并查集算法
• 4. 最终代码

1. 题目

2. 分析：每添加一条边

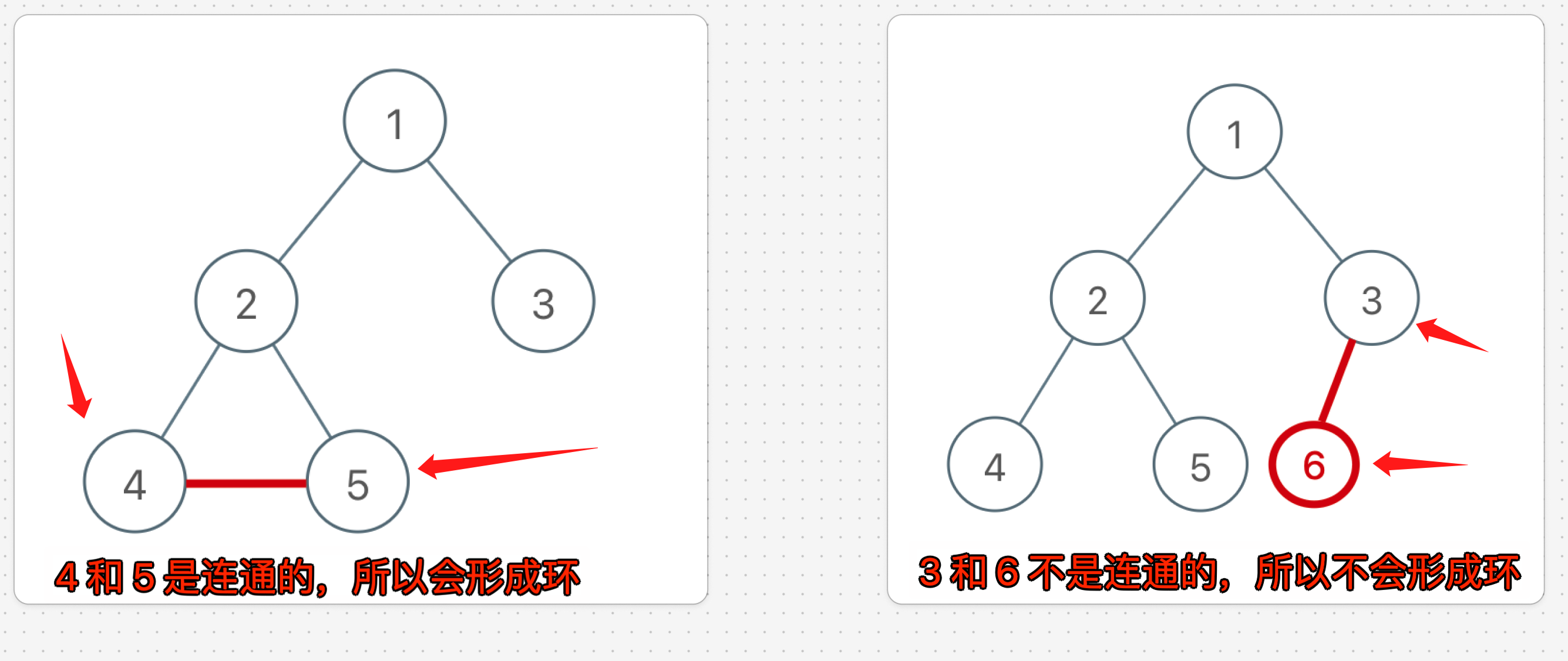
• 对于添加的这条边，如果该边的两个节点本来就在同一连通分量里，那么添加这条边会产生环；
• 反之，如果该边的两个节点不在同一连通分量里，则添加这条边不会产生环
• 而判断两个节点是否连通（是否在同一个连通分量中）就是 Union-Find 算法的拿手绝活
  • 更多参考 9. 并查集（Union Find）

3. 并查集算法

class UF {
    constructor(n) {
        // 连通分量个数
        this.count = n;
        // 存储每个节点的父节点
        this.parent = new Array(n).fill(0).map((_, index) => index);
    }
    // 将节点 p 和节点 q 连通
    union(p, q) {
        let rootP = this.find(p);
        let rootQ = this.find(q);
        if (rootP === rootQ) {
            return;
        }
        this.parent[rootQ] = rootP;
        // 两个连通分量合并成一个连通分量
        this.count--;
    }

    // 判断节点 p 和节点 q 是否连通
    connected(p, q) {
        let rootP = this.find(p);
        let rootQ = this.find(q);
        return rootP === rootQ;
    }

    find(x) {
        if (this.parent[x] !== x) {
            this.parent[x] = this.find(this.parent[x]);
        }
        return this.parent[x];
    }

    // 返回图中的连通分量个数
    getCount() {
        return this.count;
    }
}

4. 最终代码

var validTree = function (n, edges) {
    const uf = new UF(n);
    for (let edge of edges) {
        let [u, v] = edge;
        if (uf.connected(u, v)) {
            return false;
        }
        uf.union(u, v);
    }
    // 要保证最后只形成了一棵树，即只有一个连通分量
    return uf.getCount() === 1;
};