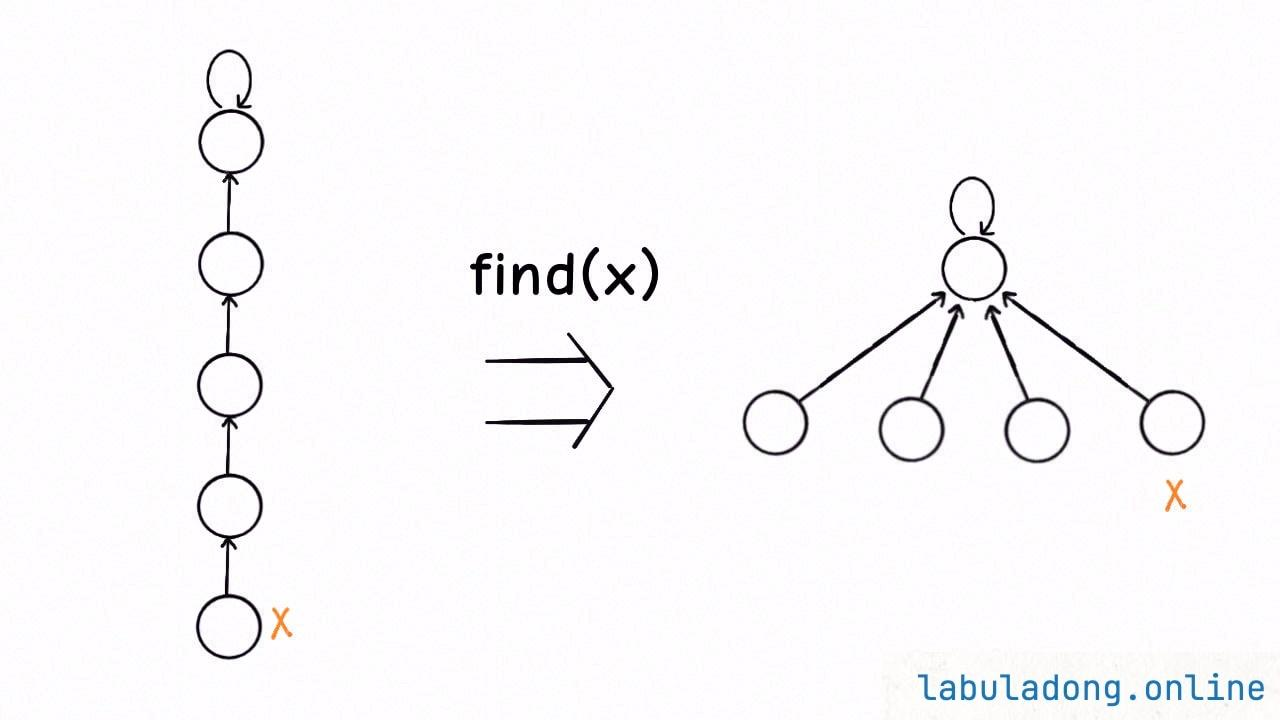
并查集（Union Find）

  • 继续整理

目录

1. 名词解释

1.1. 个连通分量

下图中每个节点自成一派，没有和其他节点相连

图片&文件

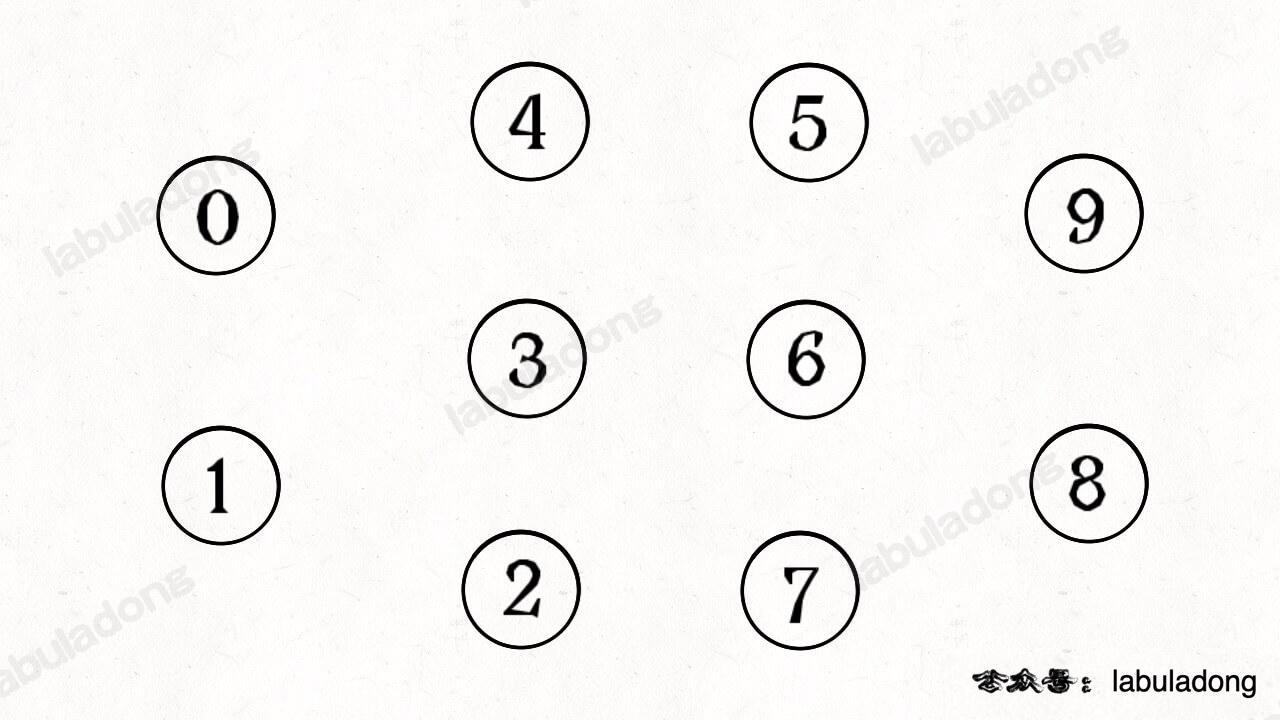
1.2. 个连通分量

  • 图结构中

图片&文件

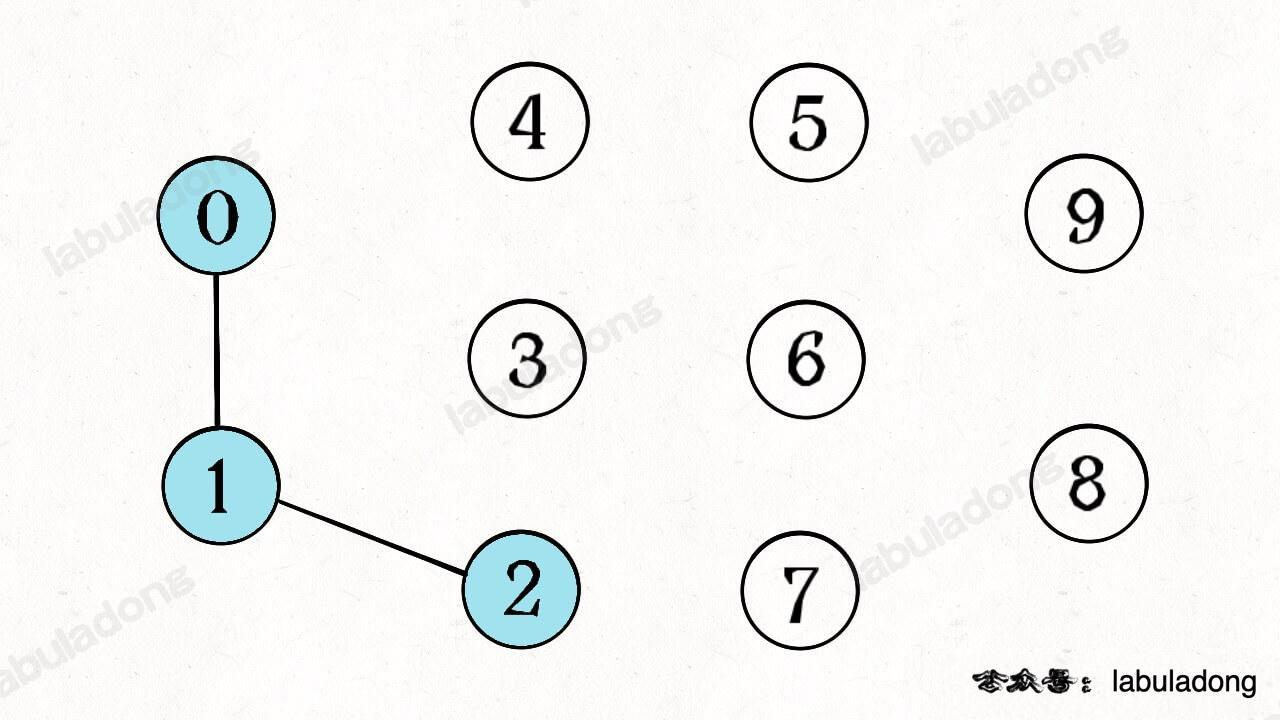
1.3. 两个节点是否连通 → 多个节点是否连通

上图中的节点 0,1,2 之间就有了连接关系，它们三个节点共同构成了一个连通分量，我们可以说这三个节点是连通的

2. 并查集（Union Find）结构

  • 并查集本质上还是树结构的延伸
  • 并查集底层其实是一片==森林==，这片==森林==由很多==多叉树==组成，==每棵树代表一个连通分量==
    • connected(p, q)：是否联通
      • 只需要判断 p 和 q 所在的多叉树的根节点
      • 若相同，则 p 和 q ==在同一棵树==中，即连通，否则不连通
    • count()：连通分量的个数
      • 只需要统计一下==总共有多少棵树==，即可得到连通分量的数量。
    • union(p, q)：连接两个点
      •  p 所在树的==根节点== →  q 所在树的根节点
interface UF {
    /**
     * 连接节点 p 和节点 q
     * @param p 节点 p
     * @param q 节点 q
     * @time O(1)
     */
    union(p: number, q: number): void;

    /**
     * 判断节点 p 和节点 q 是否连通
     * @param p 节点 p
     * @param q 节点 q
     * @returns 如果节点 p 和节点 q 在同一个连通分量中返回 true，否则返回 false
     * @time O(1)
     */
    connected(p: number, q: number): boolean;

    /**
     * 返回图中的连通分量数量
     * @returns 连通分量的数量
     * @time O(1)
     */
    count(): number;
}

3. 并查集的原理

节点结构

并查集中每个节点其实不在乎自己的子节点是谁，只在乎自己的根节点是谁，所以==节点类型==为

interface UFNode {
    // 节点 id 编号
    id: number;
    // 指向父节点的指针
    parent: UFNode;
}

平衡优化

图片&文件

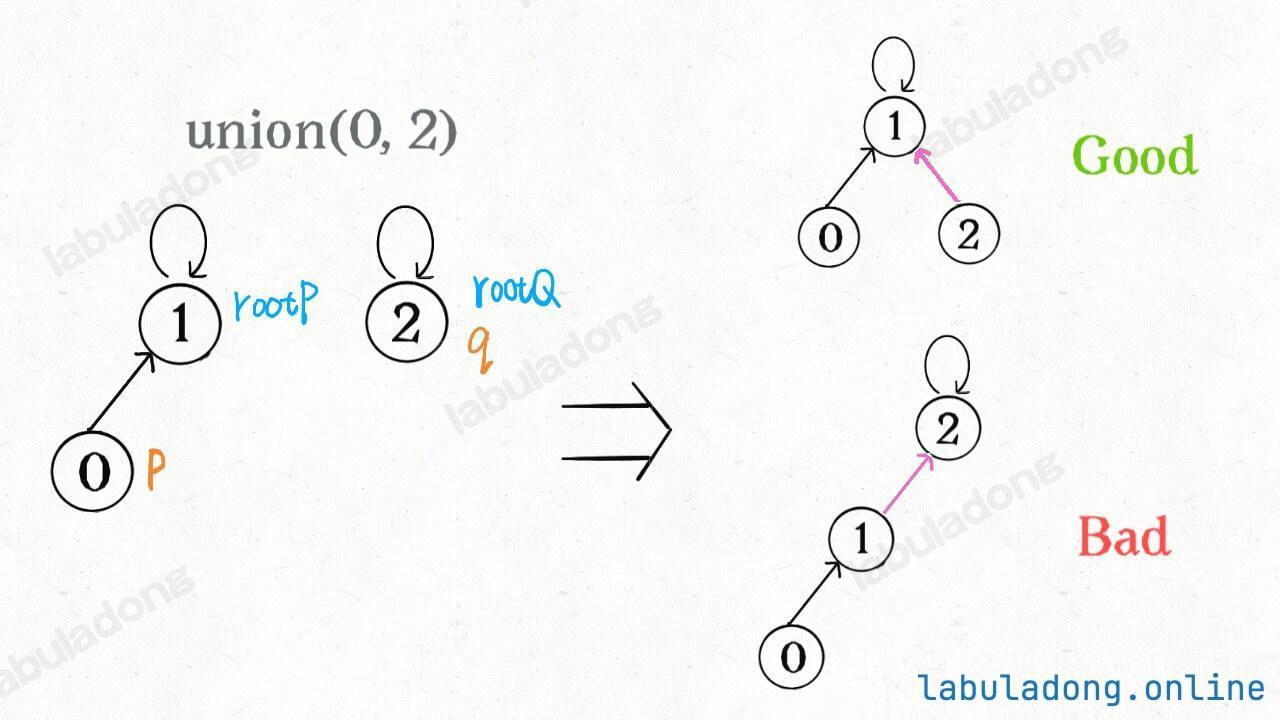
==如果能保持树高为常数==，那么上述方法的复杂度就都是 O(1) 了

  • 查找（find）：平均 O(1)
  • 合并（union）：平均 O(1)
  • 连通性判断（connected）：平均 O(1)

路径压缩

图片&文件