二叉搜索树（篇四：BST 的后序位置）

#BST #leetcode #二叉树/二叉搜索树 #2024/09/10

本文会讲解以下题目：

目录

• 1. 首先，后序有什么特殊之处？
• 2. 题目分析
• 3. 思路
• 4. 基本框架
  • 4.1. 问题
• 5. 优化
  • 5.1. 复杂度分析
• 6. 最后
• 7. 参考

1. 首先，后序有什么特殊之处？

• 前序位置的代码只能从函数参数中获取父节点传递来的数据
• 而后序位置的代码不仅可以获取参数数据，还可以拿到子树通过函数返回的值
  • 后序位置的代码，有时候可以大幅提升算法效率，比如本文需要讲解的题目

换句话说，一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

2. 题目分析

题目会给你输入一棵二叉树，请你找到节点之和最大的那棵二叉搜索树，并返回它的节点值之和。

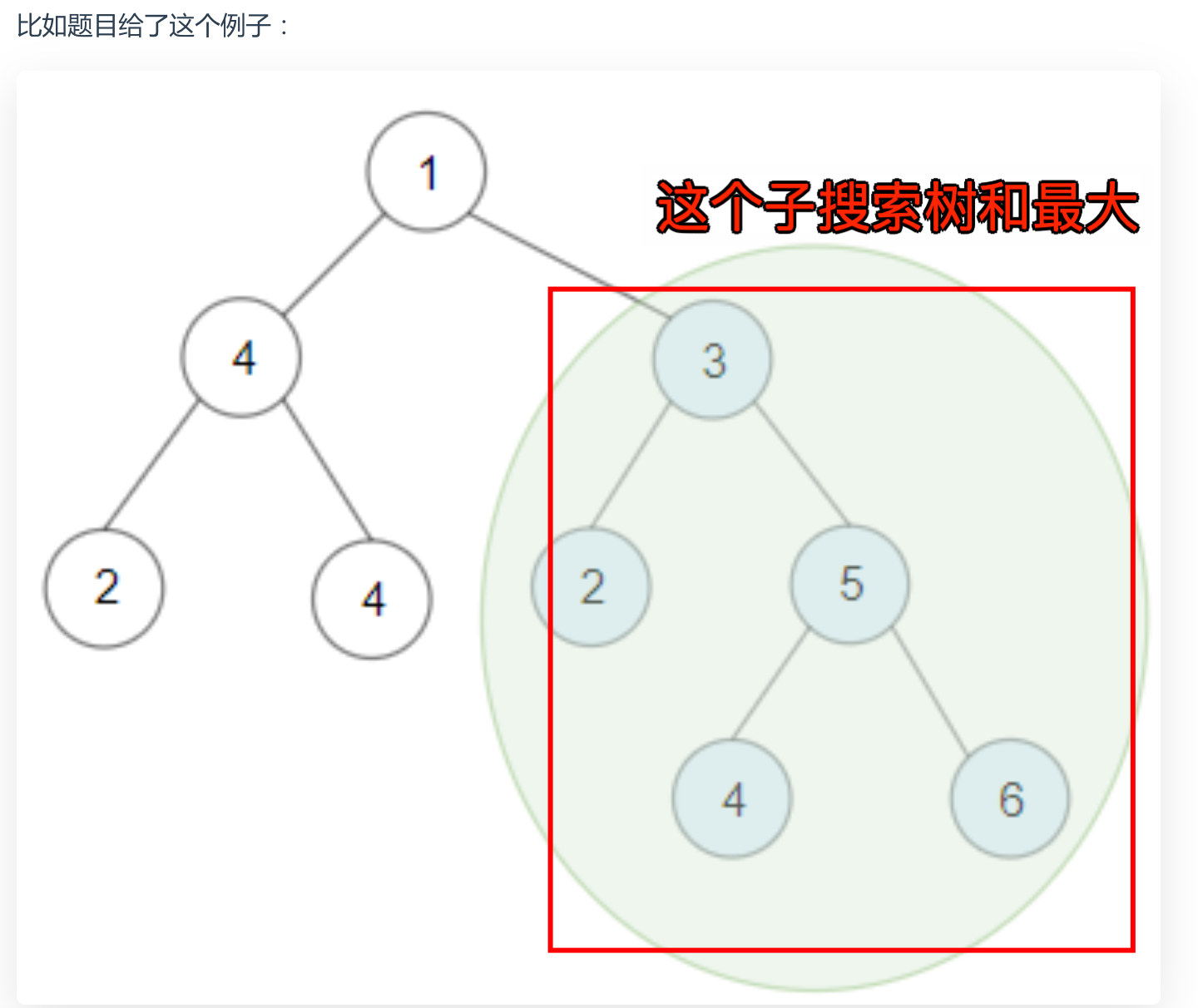
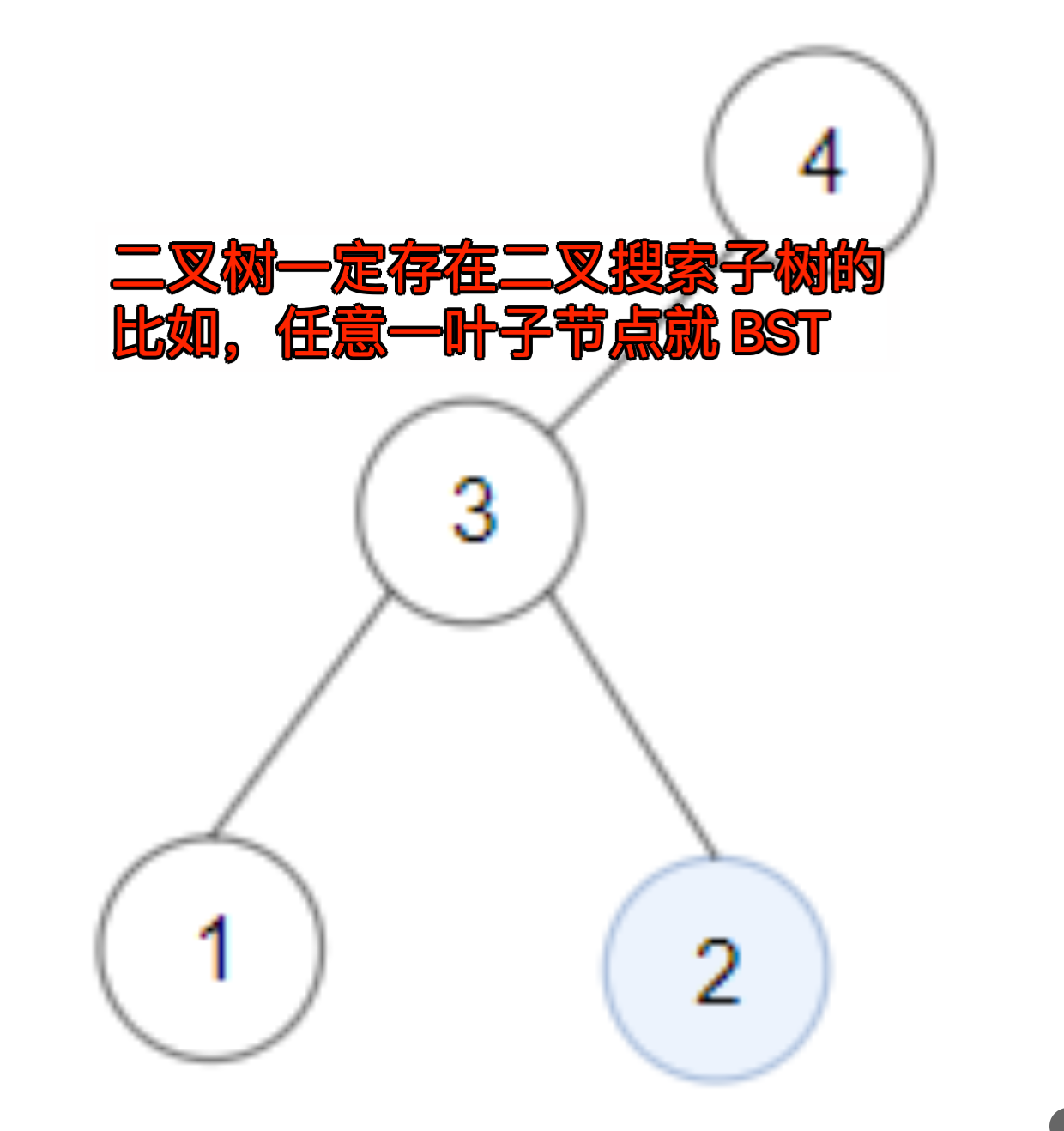
3. 思路

二叉树相关题目最核心的思路是明确当前节点需要做的事情是什么

• ① 左右子树是否是 BST
• ② 左子树的最大值 leftMax 和右子树的最小值 rightMin，为了 ③ 的判断
• ③ 左右子树的节点值之和 rootSum， 为了判断 左右子树+该节点 是否是 BST

4. 基本框架

var maxSumBST = function () {
  // 全局变量，记录 BST 最大节点之和
  var maxSum = 0;

  // 遍历二叉树
  var traverse = function (root) {
    if (root === null) {
      return;
    }
    // ******* 前序遍历位置 *******
    // ① 判断左右子树是不是 BST 二叉搜索树
    if (isBST(root.left) && isBST(root.right)) {
      // ② 计算左子树的最大值和右子树的最小值
      var leftMax = findMax(root.left);
      var rightMin = findMin(root.right);
      // ③ 判断以 root 节点为根的树是不是 BST
      if (root.val > leftMax && root.val < rightMin) {
        // 如果条件都符合，计算当前 BST 的节点之和
        var leftSum = findSum(root.left);
        var rightSum = findSum(root.right);
        var rootSum = leftSum + rightSum + root.val;
        // 计算 BST 节点的最大和
        maxSum = Math.max(maxSum, rootSum);
      }
    }
    // 二叉树遍历框架，遍历子树节点
    traverse(root.left);
    traverse(root.right);
  };

  traverse(root);
  return maxSum;
};

// 计算以 root 为根的二叉树的最大值
var findMax = function (root) {};

// 计算以 root 为根的二叉树的最小值
var findMin = function (root) {};

// 计算以 root 为根的二叉树的节点和
var findSum = function (root) {};

// 判断以 root 为根的二叉树是否是 BST
var isBST = function (root) {};

4.1. 问题

这几个辅助函数都是递归函数，递归里套递归，复杂度极高，O(N^2)

5. 优化

前序改成后序，后序遍历的时候，让 traverse 函数把辅助函数做的事情顺便做掉

var maxSumBST = function (root) {
  // 记录 BST 最大节点之和
  var maxSum = 0;

  // 计算以 root 为根的二叉树的最大值、最小值、节点和
  /**
   * @description 计算以 root 为根的二叉树的 [最大值、最小值、节点和]
   * @param {TreeNode} root
   * @return {Array} 
   * [是否 BST（0 不是，1 是）, 所有节点中的最小值, 所有节点中的最大值, 所有节点值之和]
   */
  var findMaxMinSum = function (root) {
    // base case
    if (root === null) {
      return [1, Number.MAX_SAFE_INTEGER, Number.MIN_SAFE_INTEGER, 0];
    }

    // 递归计算左右子树
    var left = findMaxMinSum(root.left);
    var right = findMaxMinSum(root.right);

    // ******* 后序遍历位置 *******
    // 通过 left 和 right 推导返回值
    // 并且正确更新 maxSum 变量
    var res = [0, 0, 0, 0];
    // 若左右子树都是 BST，且 root 大于左子树的最大值，小于右子树的最小值
    // 则以 root 为根的二叉树是 BST, 更新 res
    if (
      left[0] === 1 &&
      right[0] === 1 &&
      root.val > left[2] &&
      root.val < right[1]
    ) {
      // 以 root 为根的二叉树是 BST
      res[0] = 1;
      // 计算以 root 为根的这棵 BST 的最小值
      res[1] = Math.min(left[1], root.val);
      // 计算以 root 为根的这棵 BST 的最大值
      res[2] = Math.max(right[2], root.val);
      // 计算以 root 为根的这棵 BST 所有节点之和
      res[3] = left[3] + right[3] + root.val;
      // 更新全局变量
      maxSum = Math.max(maxSum, res[3]);
      // 否则，以 root 为根的二叉树不是 BST
    } else {
      // 以 root 为根的二叉树不是 BST
      res[0] = 0;
      // 其他的值都没必要计算了，因为用不到
    }
    return res;
  };
  findMaxMinSum(root);
  return maxSum;
};

5.1. 复杂度分析

时间复杂度只有 O(N)

6. 最后

为什么这道题用后序遍历有奇效呢，因为我们需要的这些变量全都可以通过子问题的结果推到出来，适合用分解问题的思路求解。比如

• 计算以 root 为根的二叉树的节点之和，是不是可以通过左右子树的和加上 root.val 计算出来？
• 计算以 root 为根的二叉树的最大值/最小值，是不是可以通过左右子树的最大值/最小值和 root.val 比较出来？
• 判断以 root 为根的二叉树是不是 BST，是不是得先判断左右子树是不是 BST？是不是还得看看左右子树的最大值和最小值？

7. 参考

https://labuladong.online/algo/data-structure/bst-part4/