验证二叉搜索树

98. 验证二叉搜索树

目录

• 总结
• 遍历的思路：中序遍历是升序的
• 分解问题的思路
  • 2.1. 注意点

总结

• 使用中序遍历，更容易搞定和理解

遍历的思路：中序遍历是升序的

• 如果 isValid 已经为 false 了，那么就不用再遍历了
• 注意：if (prev && prev >= root.val) 中
  • 因为 prev 为 0，条件判断会失败，所以需要改成
    • if (prev !=null && prev >= root.val) {

var isValidBST = function (root) {
  let isValid = true;
  let prev = null;
  function traverse(root) {
    if (!root || !isValid) return;
    traverse(root.left);
    if (prev !=null && prev >= root.val) {
      isValid = false;
      return;
    }
    prev = root.val;
    traverse(root.right);
  }
  traverse(root);
  return isValid;
};

分解问题的思路

• 判断 BST 的合法性
  • 对于每一个节点 root，代码值检查了它的左右孩子节点是否符合左小右大的原则
  • 最重要的是，还需要检查 root 的整个左子树都要小于 root.val，整个右子树都要大于 root.val

否则规避下面的情况：

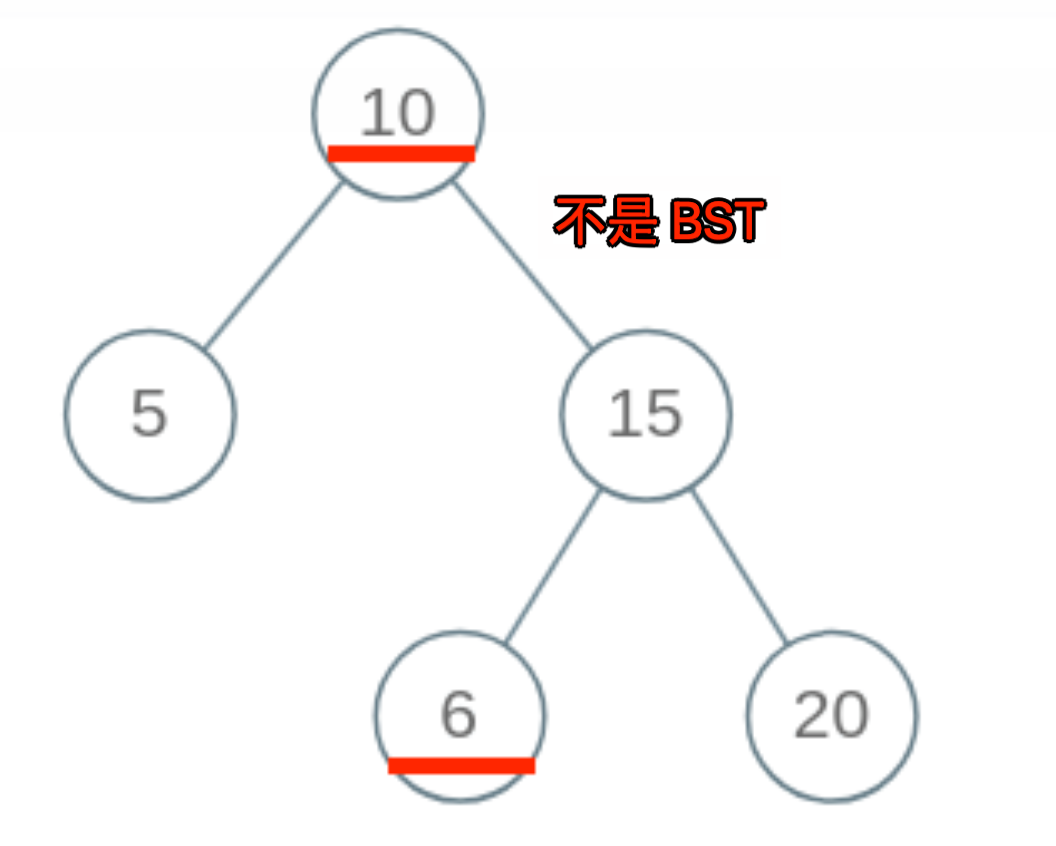
需要需要在递归函数中传值 ，具体代码如下：

var isValidBST = function (root) {
  return _isValidBST(root, Number.MIN_SAFE_INTEGER, Number.MAX_SAFE_INTEGER);
};

/**
 * @description 判断一棵树是否是二叉搜索树
 * @param {TreeNode} root 二叉树根节点
 * @param {number} min 代表 root.val 的下界
 * @param {number} max 代表 root.val 的上界
 * @return {boolean} 是否是二叉搜索树
 */
var _isValidBST = function (root, min, max) {
  // base case: root 为 null 时，是二叉搜索树
  if (root === null) {
    return true;
  }
  // 若 root.val 不符合 min < root.val < max，说明不是二叉搜索树
  if (root.val <= min || root.val >= max) {
    return false;
  }

  // 递归判断左右子树是否是二叉搜索树
  // 左子树的最大值为 root.val, 最小值为 min
  let left = _isValidBST(root.left, min, root.val);
  // 右子树的最小值为 root.val, 最大值为 max
  let right = _isValidBST(root.right, root.val, max);

  return left && right;
};

2.1. 注意点

上面代码的 18 行中，需要注意使用 >=，还有一些注意点如下图：