缺失的第一个正数：找第一个缺失的正整数

#leetcode #算法

目录

• 思路
• 1. 题目及理解
• 2. 思路一
  • 2.1. 举个例子
• 3. 代码实现
• 4. 复杂度分析

思路

• 将所有小于等于0或大于n的数替换为n+1
• 遍历一遍：
  • 每个元素都放他的负数，表示这个数出现过
  • 如果大于 0 说明没出现过
• 找到==第一个正数==，其索引 +1 就是缺失的最小正数

1. 题目及理解

41. 缺失的第一个正数

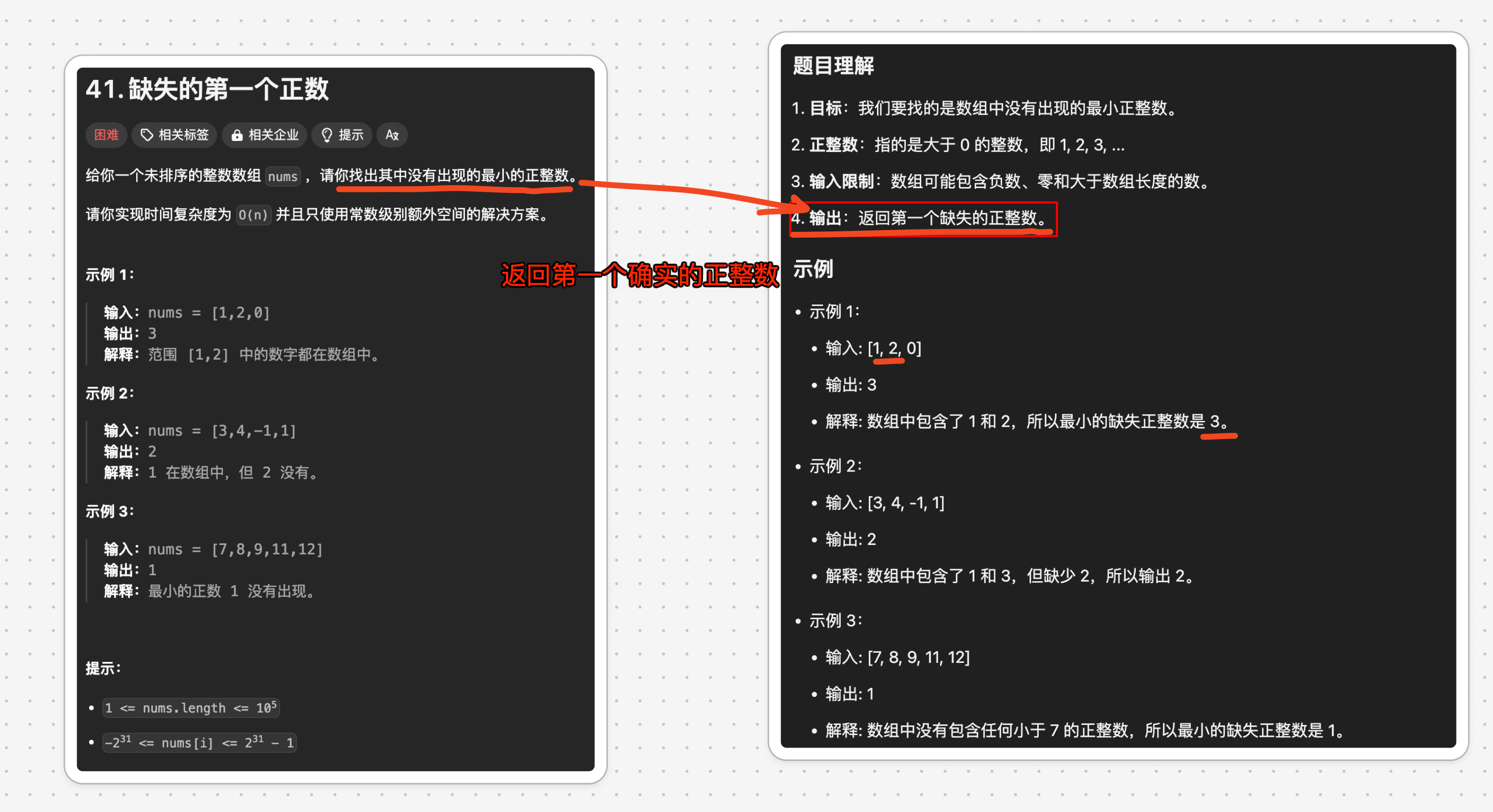
2. 思路一

1. 范围分析：
   • 最小的缺失正整数一定在 [1, n+1] 之间，其中 n 是数组的长度。
   • 如果数组包含了从 1 到 n 的所有数，那么缺失的正整数就是 n+1。
2. 原地修改数组：把每个已经存在的数变成它的负数
3. 查找缺失的数：
   • 在重新排列数组后，遍历数组
   • 找到第一个位置 i 使得 nums[i] != i + 1，则 i + 1 就是缺失的最小正整数。

2.1. 举个例子

• 初始数组：[3, 4, -1, 1] 数组长度 n = 4
• 预处理（将不在 [1, n] 范围内的数替换为 n+1：
  • -1 被替换为 5 (n+1) 结果：[3, 4, 5, 1]
• 原地修改数组：把每个已经存在的数变成它的负数
  • 已经存在的数：即 <= n = 4 的数
  • 其他的数不变
• 找到大于 0 的数，返回它的索引+1

3. 代码实现

/**  
 * @param {number[]} nums  
 * @return {number}  
 */  
var firstMissingPositive = function (nums) {  
    const n = nums.length;  
    // Step 1: 将所有小于等于0或大于n的数替换为n+1  
    for (let i = 0; i < n; i++) {  
        if (nums[i] <= 0 || nums[i] > n) {  
            nums[i] = n + 1;  
        }  
    }  
    // Step 2: 使用原地哈希，将每个数放到对应的位置  
    // ::::放他的负数，表示这个数出现过，如果大于 0 说明没出现过 ::::    
    for (let i = 0; i < n; i++) {  
        let num = Math.abs(nums[i]);  
        // 如果 num <= n，将 nums[num-1] 变为负数  
        // 说明 num 出现过  
        if (num <= n) {  
            nums[num - 1] = -Math.abs(nums[num - 1]);  
        }  
        // 还是正数，说明 num 没出现过  
    }  
    // Step 3: 找到第一个正数，其索引 +1 就是缺失的最小正数  
    for (let i = 0; i < n; i++) {  
        if (nums[i] > 0) {  
            return i + 1;  
        }  
    }  
    // 如果没有找到，则返回n+1  
    return n + 1;  
};

4. 复杂度分析

时间复杂度分析：

1. 第一个循环：O(n)
   • 遍历整个数组一次，将不在 [1, n] 范围内的数替换为 n+1。
2. 第二个循环：O(n)
   • 再次遍历整个数组，进行原地哈希标记。
3. 第三个循环：O(n)
   • 最后一次遍历数组，寻找第一个正数。 总时间复杂度：O(n) + O(n) + O(n) = O(n)

空间复杂度分析：

• 这个算法使用了原地修改的技巧，没有使用任何额外的数据结构。
• 只使用了几个额外的变量（如 n, i, num），这些变量的空间是常数级的。 总空间复杂度：O(1)

复杂度分析总结：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

这个算法的优点在于：

1. 时间效率高：只需线性时间就能解决问题。
2. 空间效率高：通过原地修改数组，避免了使用额外空间。