合并区间

#leetcode #2024/08/18 #算法/区间问题

56. 合并区间

目录

• 关键点
• 1. 题目及理解
• 2. 思路一：区间问题
  • 2.1. 代码实现
  • 2.2. 复杂度分析
• 3. 错误记录

关键点

• 先按照区间的起始位置排序，升序排序
• 如果起始位置相同，则按照结束位置降序排序

1. 题目及理解

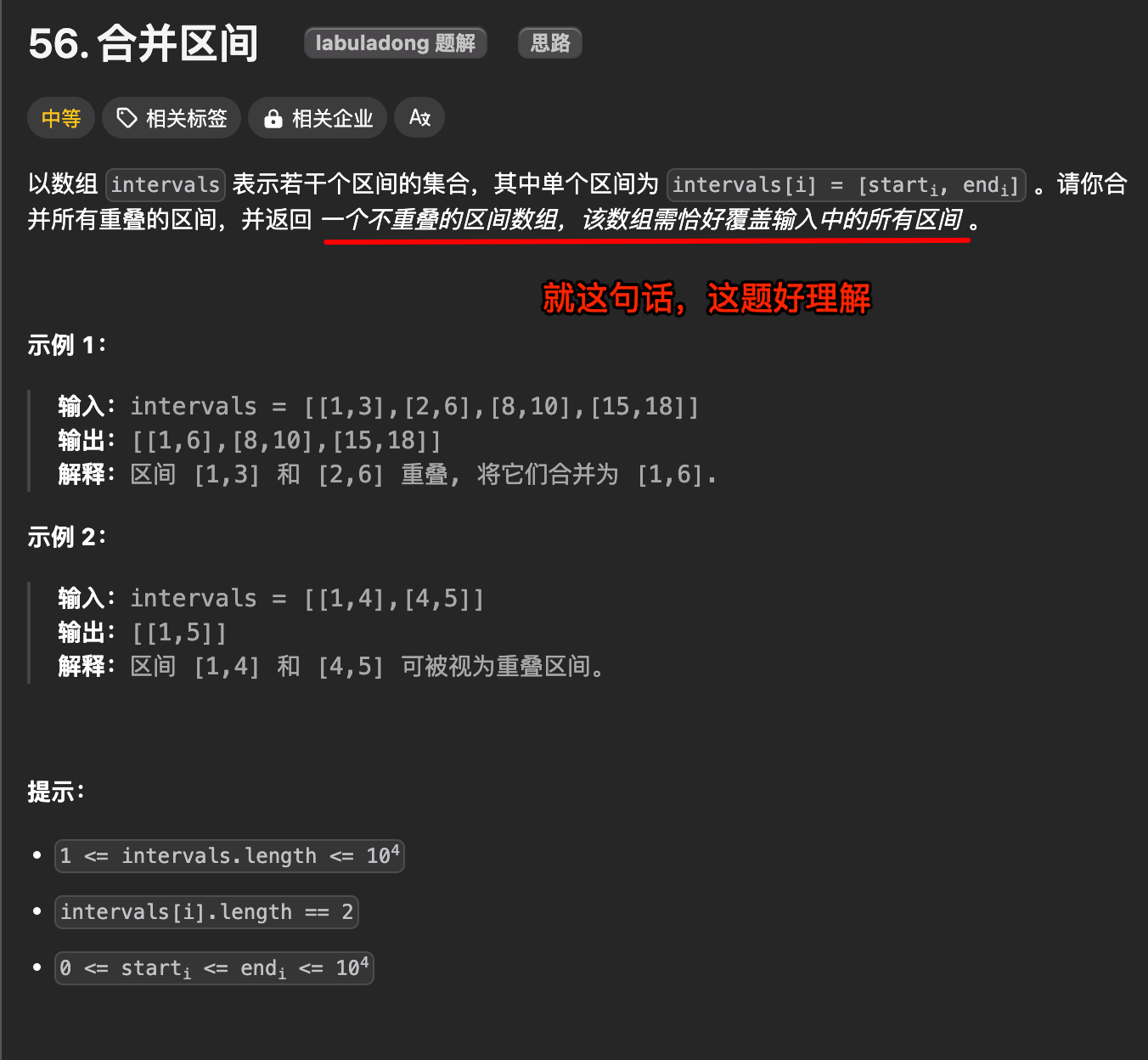
2. 思路一：区间问题

所谓区间问题，就是线段问题，让你合并所有线段、找出线段的交集等等。主要有两个技巧：

1. 排序
   • 先按照起点升序排序，
   • 若起点相同，则按照终点降序排序。
   • 
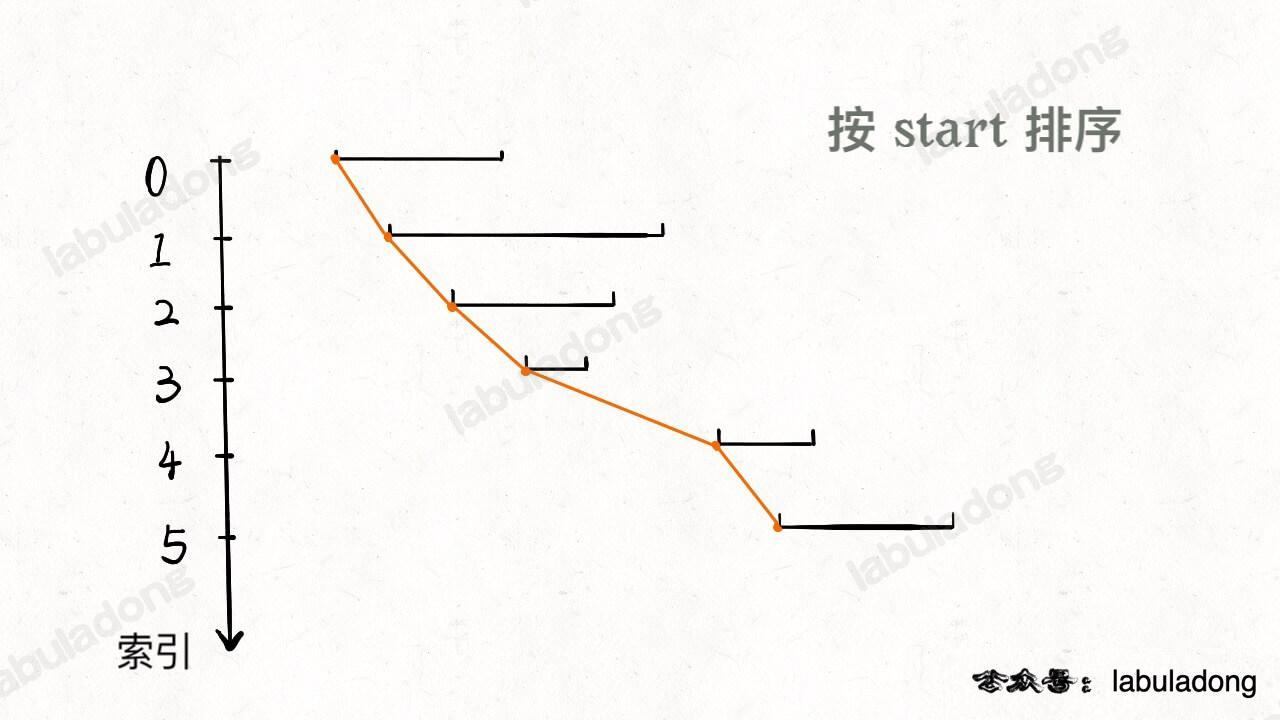
2. 画图。就是说不要偷懒，勤动手，两个区间的相对位置到底有几种可能，不同的相对位置我们的代码应该怎么去处理，如下图：

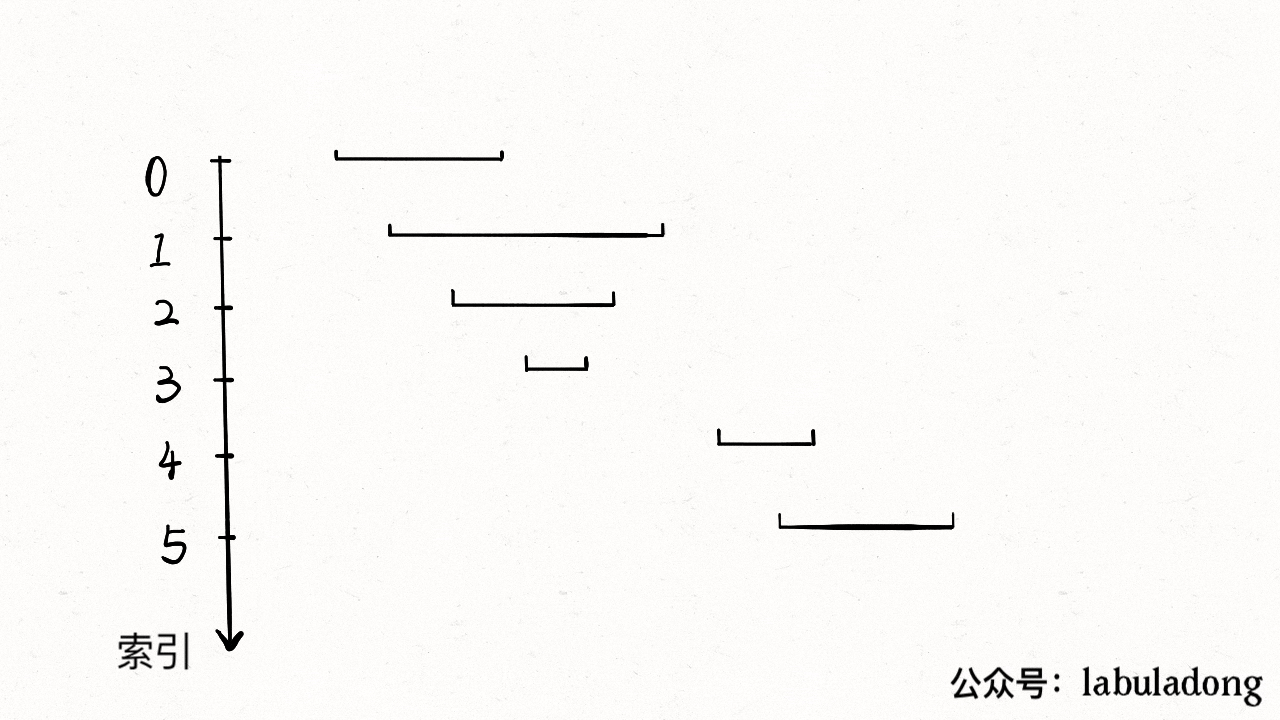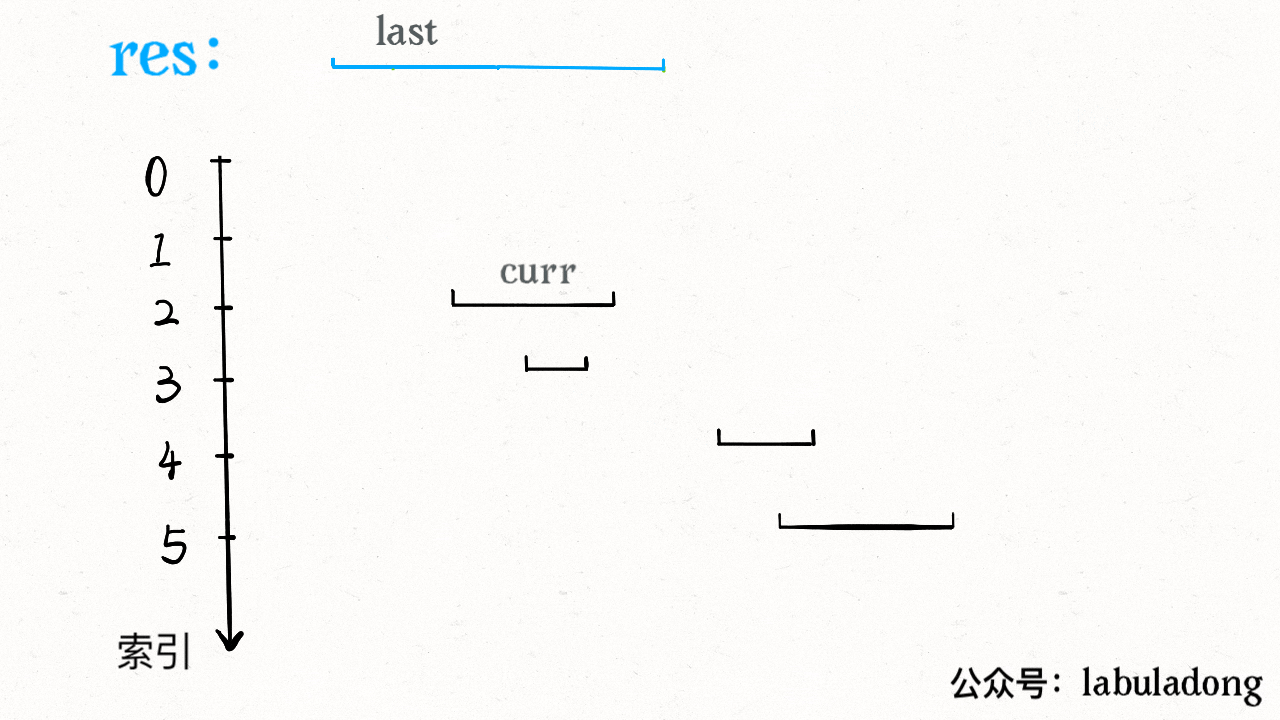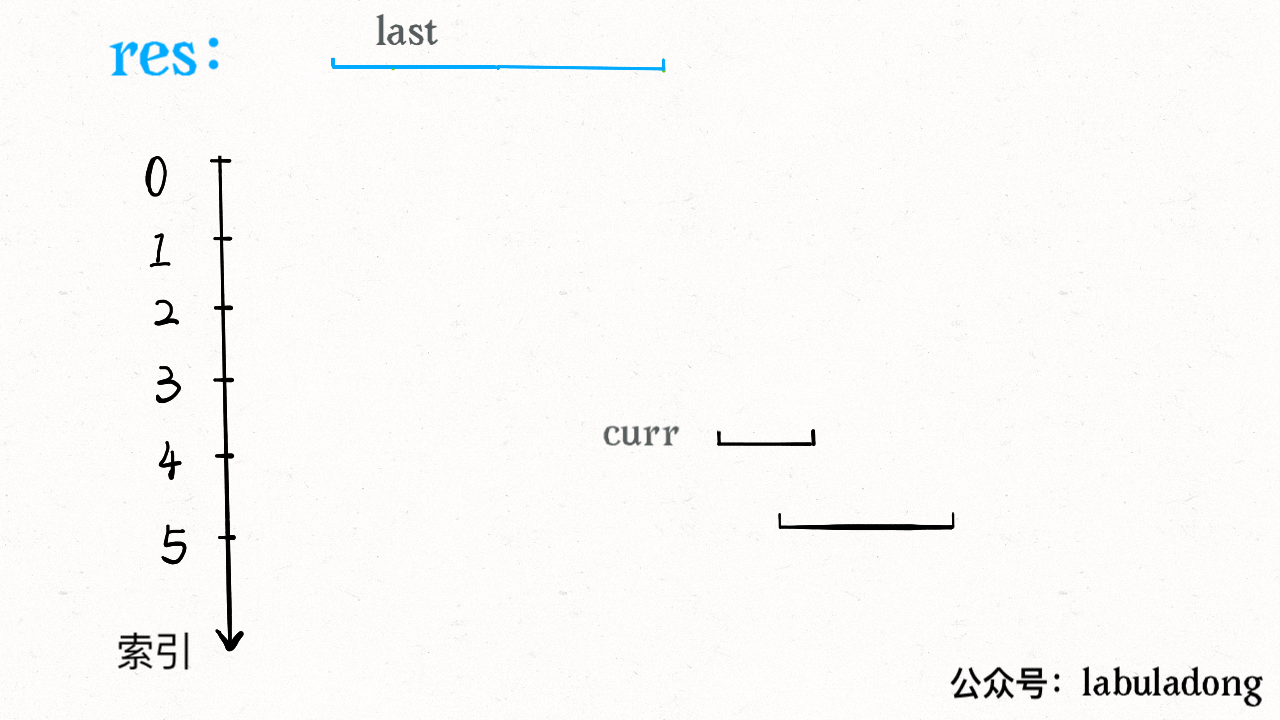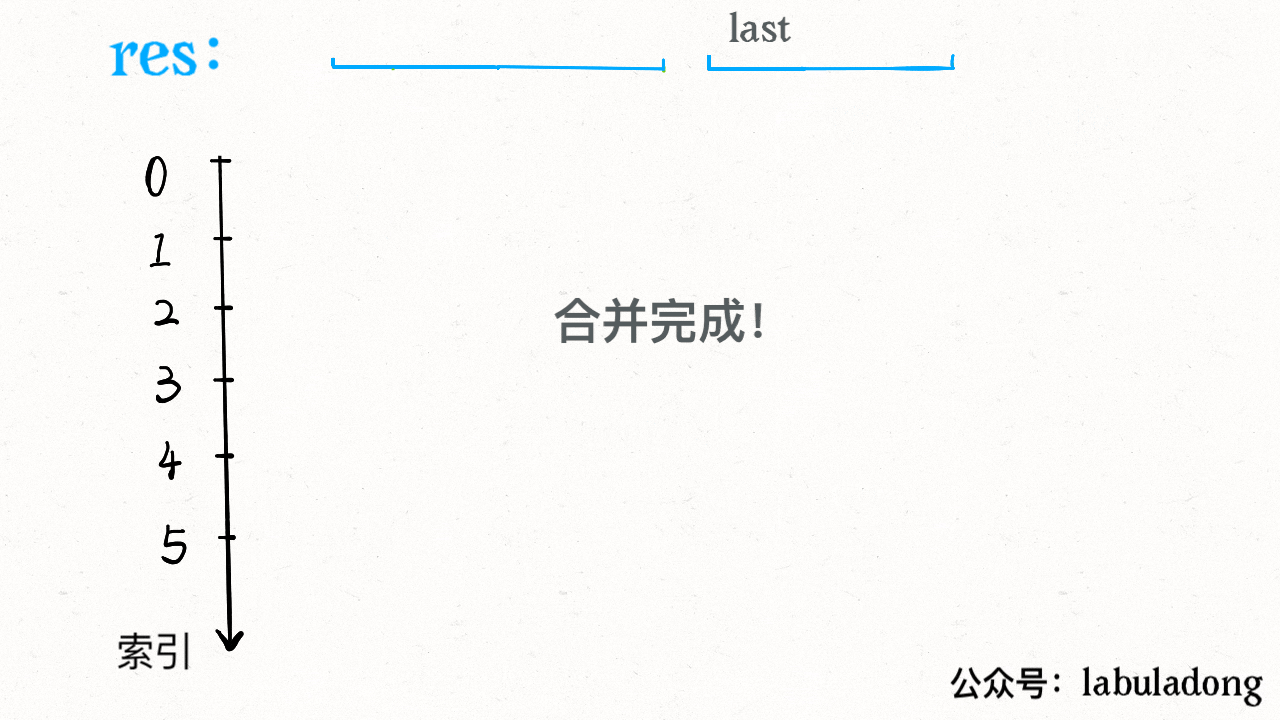
最终如下图：

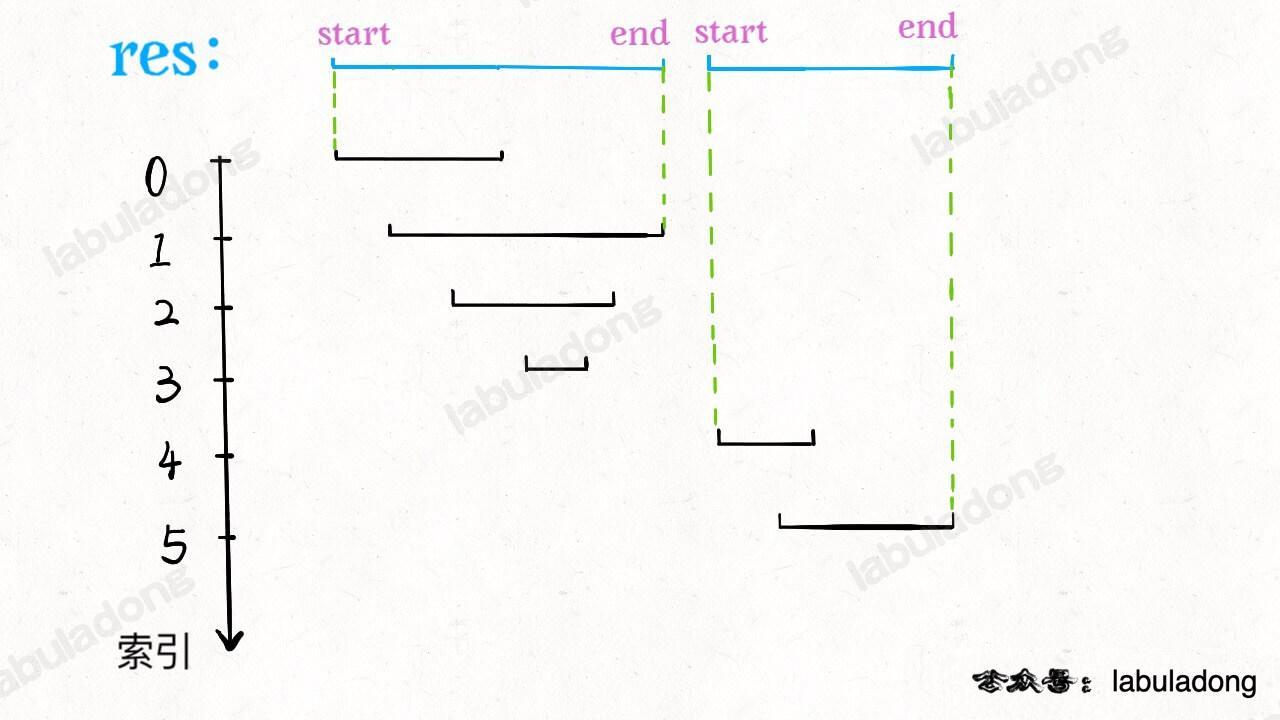
2.1. 代码实现

/**
 * @description 合并区间
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function (intervals) {
  let res = [];
  //:::: ① 先按照区间的起始位置排序，升序排序,如果起始位置相同，则按照结束位置降序排序
  intervals.sort((a, b) => a[0] - b[0] || b[1] - a[1]);

  // 因为已经按照区间的起始位置排序了，所以可以直接将第一个区间放入结果数组中
  res.push(intervals[0]);
  //:::: ② 遍历区间数组
  for (let i = 1; i < intervals.length; i++) {
    let currInterval = intervals[i];
    // 获取结果数组中最后一个区间
    let lastInterval = res[res.length - 1];

    //:::: ③ 判断当前区间的起始位置是否小于等于结果数组中最后一个区间的结束位置
    // 如果小于等于，则说明两个区间有重叠，可以合并
    if (currInterval[0] <= lastInterval[1]) {
      //:::: ④ 更新结果数组中最后一个区间的结束位置
      // 更新为当前区间的结束位置和结果数组中最后一个区间的结束位置的最大值
      lastInterval[1] = Math.max(lastInterval[1], currInterval[1]);
    } else {
      //:::: ⑤ 如果不重叠，则直接将当前区间放入结果数组中
      res.push(currInterval);
    }
  }
  return res;
};

2.2. 复杂度分析

时间复杂度分析：

1. 排序：使用了 JavaScript 的内置排序方法，时间复杂度为 O(n log n)，其中 n 是区间的数量。
2. 遍历区间：一次线性遍历，时间复杂度为 O(n)。
3. 总的时间复杂度：O(n log n) + O(n) = O(n log n)，主要由排序步骤决定。

空间复杂度分析：

1. 结果数组 res：在最坏情况下（没有重叠的区间），可能需要存储所有的输入区间，空间复杂度为 O(n)。
2. 排序：JavaScript 的排序算法通常使用额外的 O(log n) 到 O(n) 的空间。
3. 总的空间复杂度：O(n)，主要由结果数组和排序过程决定。

3. 错误记录

[!danger] Array.sort 升序为 a - b ，降序为 b - a

• 先升
• 若相同，再降序 a[0] - b[0] || b[1] - a[1]

// 按照区间的起始位置排序，升序排序,如果起始位置相同，则按照结束位置降序排
intervals.sort((a, b) => a[0] - b[0] || b[1] - a[1]);