动态规划和回溯算法:单词拆分与单词拆分 II
#算法/动态规划 #回溯算法
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 140. Word Break II | 140. 单词拆分 II | 🔴 |
| 139. Word Break | 139. 单词拆分 | 🟠 |
目录
1. 单词拆分
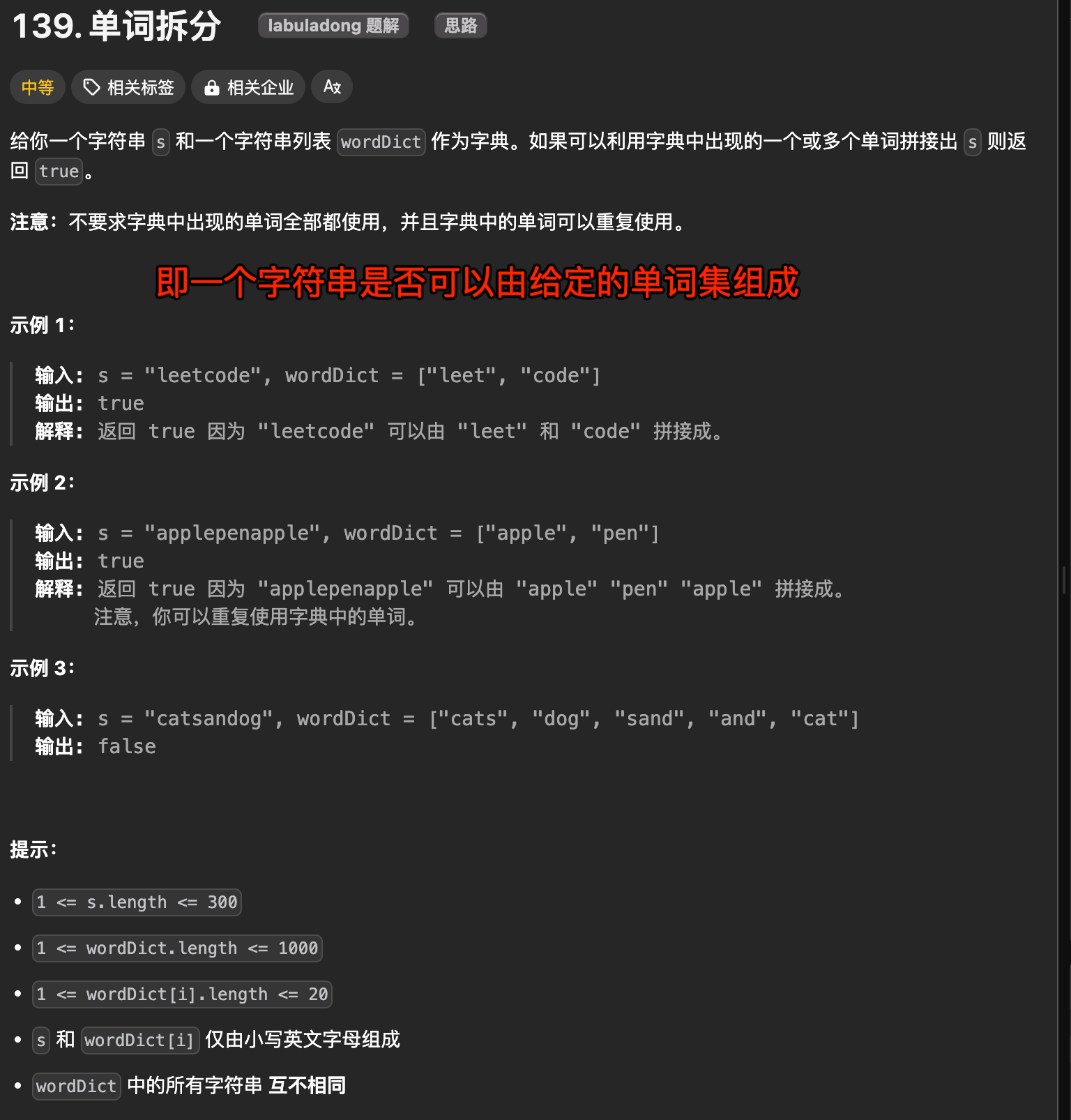
1.1. 回溯算法
var wordBreak = function (s, wordDict) {
let found = false;
// 记录搜索过程中的路径
let track = [];
// 参数 s 表示当前搜索到的字符串
// 参数 i 表示当前搜索到 s 中的第 i 个字符
// 递归函数的定义:对于 s[i..] 这个后缀字符串,从 s[i] 开始搜索 wordDict
function backtrack(s, i) {
// base case
if (found) {
// 如果已经找到答案,就不要再递归搜索了
return;
}
if (i == s.length) {
// 整个 s 都被匹配完成,找到一个合法答案
found = true;
return;
}
// 回溯算法框架
for (let word of wordDict) {
// 看看哪个单词能够匹配 s[i..] 的前缀
let len = word.length;
// 代表从 i 开始的一个单词,长度为 len,看看是不是等于 word
let newWord = s.substring(i, i + len);
if (i + len <= s.length && newWord == word) {
// 找到一个单词匹配 s[i..i+len)
// 做选择
track.push(word);
// 进入回溯树的下一层,继续匹配 s[i+len..]
backtrack(s, i + len);
// 撤销选择
track.pop();
}
}
}
backtrack(s, 0);
return found;
};
这段代码无法通过所有测试用例
1.2. 回溯算法:剪枝
var wordBreak = function (s, wordDict) {
let found = false;
// 记录搜索过程中的路径
let track = [];
// 记录不能切分的子串
let memo = new Set();
// 参数 s 表示当前搜索到的字符串
// 参数 i 表示当前搜索到 s 中的第 i 个字符
// 递归函数的定义:对于 s[i..] 这个后缀字符串,从 s[i] 开始搜索 wordDict
function backtrack(s, i) {
// base case
if (found) {
// 如果已经找到答案,就不要再递归搜索了
return;
}
if (i == s.length) {
// 整个 s 都被匹配完成,找到一个合法答案
found = true;
return;
}
// 当前子串(子树)不能被切分,就不用继续递归了
// 新增的剪枝逻辑,查询子串(子树)是否已经计算过
let suffix = s.substring(i);
if (memo.has(suffix)) {
// 当前子串(子树)不能被切分,就不用继续递归了
return;
}
// 回溯算法框架
for (let word of wordDict) {
// 看看哪个单词能够匹配 s[i..] 的前缀
let len = word.length;
// 代表从 i 开始的一个单词,长度为 len,看看是不是等于 word
let newWord = s.substring(i, i + len);
if (i + len <= s.length && newWord == word) {
// 找到一个单词匹配 s[i..i+len)
// 做选择
track.push(word);
// 进入回溯树的下一层,继续匹配 s[i+len..]
backtrack(s, i + len);
// 撤销选择
track.pop();
// 后序位置,将不能切分的子串(子树)记录到备忘录
if (!found) {
memo.add(suffix);
}
}
}
}
backtrack(s, 0);
return found;
};
1.3. 动态规划:递归
- 对于
s- 如果能够从
wordDict中找到一个单词匹配s的前缀s[0..k]- 那么只要我能拼出
s[k+1..],就一定能拼出整个s
- 那么只要我能拼出
- 如果能够从
规模较大的原问题 wordBreak(s[0..]) 分解成了规模较小的子问题 wordBreak(s[k+1..])
1.3.1. dp 函数定义
// 定义:返回 s[i..] 是否能够被拼出
function dp(s, i) {}
// 计算整个 s 是否能被拼出,调用 dp(s, 0)
1.3.2. 完整代码
var wordBreak = function(s, wordDict) {
// 用哈希集合方便快速判断是否存在
let wordSet = new Set(wordDict);
// 备忘录,-1 代表未计算,0 代表无法凑出,1 代表可以凑出
let memo = Array(s.length).fill(-1);
// 主函数
function dp(i) {
// base case
if (i == s.length)
return true;
// 防止冗余计算
if (memo[i] !== -1)
return memo[i] == 0 ? false : true;
// 遍历 s[i..] 的所有前缀
for (let j = i + 1; j <= s.length; j++) {
// 看看哪些前缀存在 wordDict 中
let prefix = s.substring(i, j);
if (wordSet.has(prefix)) {
// 找到一个单词匹配 s[i..j)
// 只要 s[j..] 可以被拼出,s[i..] 就能被拼出
if (dp(j)) {
memo[i] = 1;
return true;
}
}
}
// s[i..] 无法被拼出
memo[i] = 0;
return false;
}
return dp(0);
};
2. 单词拆分 II
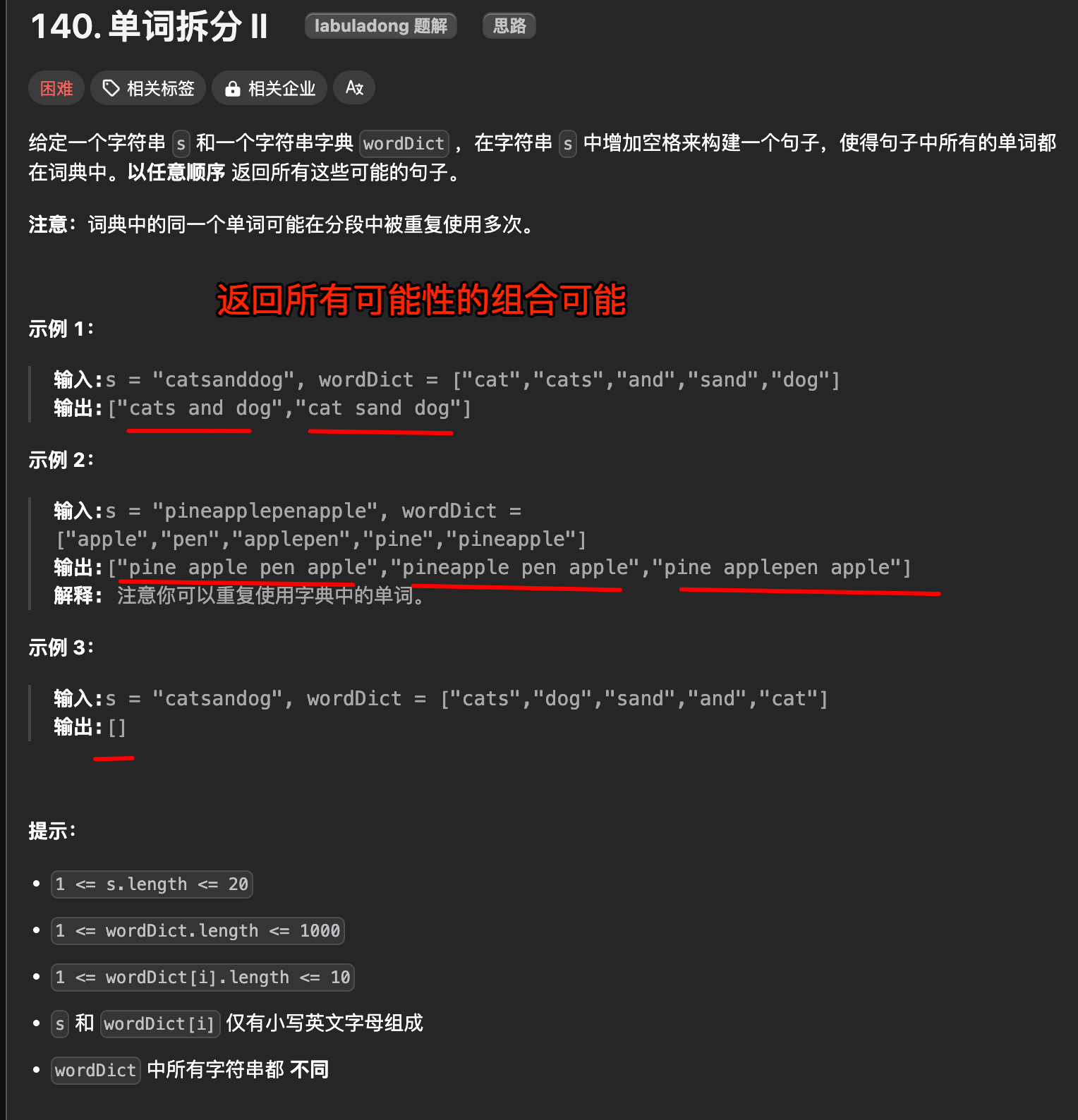
这道题不是单单问你 s 是否能被拼出,还要问你是怎么拼的
2.1. 回溯算法思路(遍历的思路)
基于上面的代码,添加以下行即可
var wordBreak = function (s, wordDict) {
// 记录结果
let res = [];
// 记录回溯算法的路径
let track = [];
// 回溯算法框架
function backtrack(i) {
// base case
if (i === s.length) {
// 找到一个合法组合拼出整个 s,转化成字符串
res.push(track.join(" "));
return;
}
// 回溯算法框架
for (let word of wordDict) {
// 看看哪个单词能够匹配 s[i..] 的前缀
let length = word.length;
if (i + length <= s.length && s.substring(i, i + length) === word) {
// 找到一个单词匹配 s[i..i+len)
// 做选择
track.push(word);
// 进入回溯树的下一层,继续匹配 s[i+len..]
backtrack(i + length);
// 撤销选择
track.pop();
}
}
}
// 执行回溯算法穷举所有可能的组合
backtrack(0);
return res;
};
2.2. 不能利用后续位置优化:剪枝
不能使用备忘录优化
因为回溯算法的 track 变量仅维护了从根节点到当前节点走过的路径,并没有记录子树的信息。
2.3. 但可以使用分解问题(动态规划)可以剪枝
var wordBreak = function(s, wordDict) {
const wordDictSet = new Set(wordDict);
// 备忘录
const memo = new Map();
// 定义:返回用 wordDict 构成 s[i..] 的所有可能
const dp = (i) => {
const res = [];
if (i === s.length) {
res.push("");
return res;
}
// 防止冗余计算
if (memo.has(i)) {
return memo.get(i);
}
// 遍历 s[i..] 的所有前缀
for (let j = i + 1; j <= s.length; j++) {
// 看看哪些前缀存在 wordDict 中
const prefix = s.slice(i, j);
if (wordDictSet.has(prefix)) {
// 找到一个单词匹配 s[i..i+len)
const suffixList = dp(j);
// 构成 s[i+len..] 的所有组合加上 prefix
// 就是构成构成 s[i] 的所有组合
suffixList.forEach((suffix) => {
const space = suffix === "" ? "" : " ";
res.push(prefix + space + suffix);
});
}
}
// 存入备忘录
memo.set(i, res);
return res;
};
return dp(0);
};
这个解法依然用备忘录消除了重叠子问题,所以 dp 函数递归调用的次数减少为 O(N)O(N),但 dp 函数本身的时间复杂度上升了,因为 subProblem 是一个子集列表,它的长度是指数级的。
再加上拼接字符串的效率并不高,且还要消耗备忘录去存储所有子问题的结果,所以从 Big O 的角度来分析,这个算法的时间复杂度并不比回溯算法低,依然是指数级别;但这个解法确实消除了重叠子问题,所以是要比回溯算法高明一些。
3. 最后
- ==动态规划的思路也可以去解决回溯算法==
- 我们处理排列组合问题时一般使用回溯算法去「遍历」回溯树,而不用「分解问题」的思路去处理,
- 因为存储子问题的结果就需要大量的时间和空间,除非重叠子问题的数量较多的极端情况,否则得不偿失。