动态规划穷举的两种视角:不同的子序列个数
#算法/动态规划
目录
- 1. 总结
- 2. 先回顾下动态规划的解题要点
- 3. 两种穷举的思路(排列组合的两个视角)
- 4. 该题分析
- 5. 盒子的视角 , 即
t 的视角 - 6. 算法复杂度分析
- 7. 小球的视角 即
s 的视角 - 8. 总结
- 9. 思考
- 10. 参考
1. 总结
1.1. 递归解法
- 错误记录:
dp[k + 1, j + 1]和dp( k+1 , j +1 )- 一个数组,一个函数,区别这么大,老是写错了
- 注意变量:
i j k分别代表什么 ,很重要
- dp 函数定义:
- ==
s[i..]的子序列中t[j..]出现的次数为dp(i, j)==
- ==
var numDistinct = function (s, t) {
let m = s.length;
let n = t.length;
function dp(i, j) {
// 全部匹配完成,说明匹配成功了,返回 1
if (j === n) {
return 1;
}
// i 后面的个数 小于 j 后面的个数,说明匹配不到子序列了,直接返回0 即可
// s[i...] 比 t[j...] 还短
if (m - i < n - j) {
return 0;
}
let res = 0;
// 在 s[i..] 中寻找 k,使得 s[k] == t[j]
for (let k = i; k < m; k++) {
if (s[k] == t[j]) {
res += dp(k + 1, j + 1);
}
}
return res;
}
return dp(0, 0);
};
带备忘录的解法
var numDistinct = function (s, t) {
// s[i..] 的子序列中 t[j..] 出现的次数为 dp(s, i, t, j)
let m = s.length;
let n = t.length;
let memo = new Array(m + 1).fill().map(() => {
return new Array(n + 1).fill(-1);
});
function dp(i, j) {
if (memo[i][j] !== -1) return memo[i][j];
// base case
// 全部匹配完成,说明匹配成功了,返回 1
if (j === n) {
return 1;
}
// i 后面的个数 小于 j 后面的个数,说明匹配不到子序列了,直接返回0 即可
// s[i...] 比 t[j...] 还短
if (m - i < n - j) {
return 0;
}
let res = 0;
// 在 s[i..] 中寻找 k,使得 s[k] == t[j]
for (let k = i; k < m; k++) {
if (s[k] == t[j]) {
res += dp(k + 1, j + 1);
}
}
memo[i][j] = res;
return res;
}
return dp(0, 0);
};
1.2. dp 数组迭代解法
[!todo] 自己再写下试试
要点:
- 为了能够正着遍历,
dp[i][j]表示s[...i]的子序列中t[...j]字符出现的次数- 而不是
s[...j]
- 而不是
- 动态转移方程
/**
* @param {string} s
* @param {string} t
* @return {number}
*/
var numDistinct = function (s, t) {
const m = s.length;
const n = t.length;
// dp[i][j] 表示 s[...i] 的子序列中 t[...j] 字符出现的次数
// 初始化为0
const dp = Array(m + 1)
.fill(0)
.map(() => Array(n + 1).fill(0));
// base case
// 当 t 为空串时,空串是任何字符串的子序列,且只有一种方案
for (let i = 0; i <= m; i++) {
dp[i][0] = 1;
}
// 填充 DP 数组
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// ① 当前字符相等时,有两种选择:
// 1.1 使用当前字符匹配:dp[i-1][j-1]
// 1.2 不使用当前字符匹配:dp[i-1][j]
if (s[i - 1] === t[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
//② 当前字符不相等,只能不使用当前字符
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[m][n];
};
2. 先回顾下动态规划的解题要点
- 明确
dp 函数或数组的定义- 从
已知的「状态」中推导出未知的「状态」
- 从
- 就算
dp 函数/数组的定义相同- 如果你使用
不同的「视角」进行穷举,效率也不见得是相同的
- 如果你使用
3. 两种穷举的思路(排列组合的两个视角)

3.1. 球盒模型
如下图:

3.2. 视角 1: 盒子的视觉
选择:
- 选择哪个盒子
- 选择之后不能再被选择
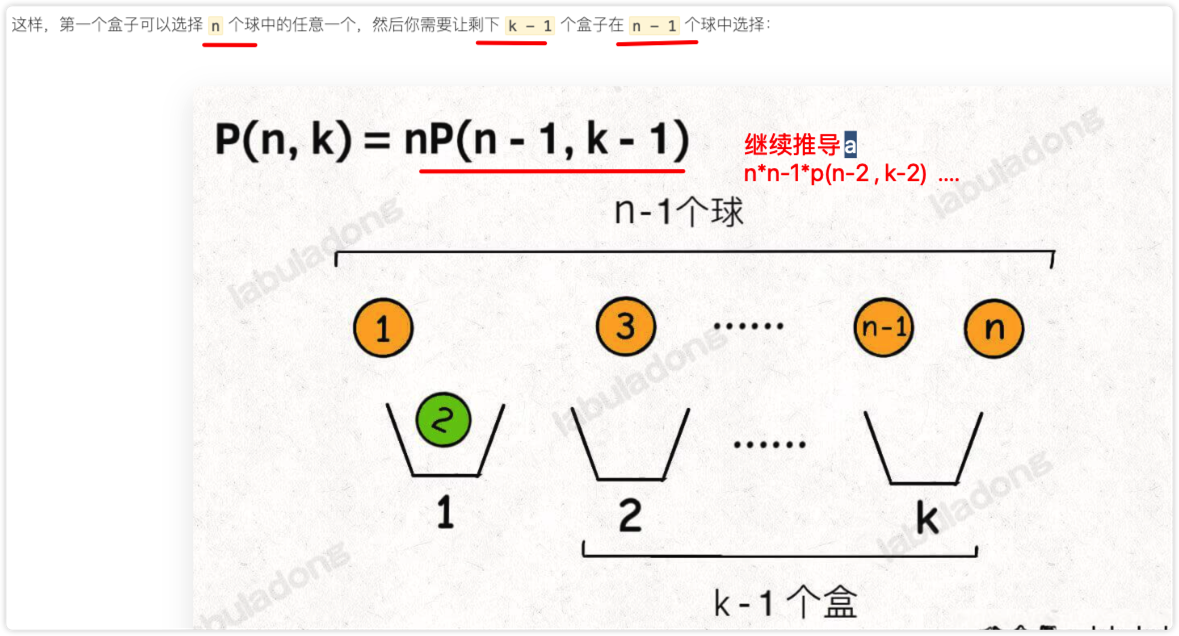
一直推导,最终结论,如上面的公式
3.3. 视角 2:球的视角
选择:
- 放入
- 不放入
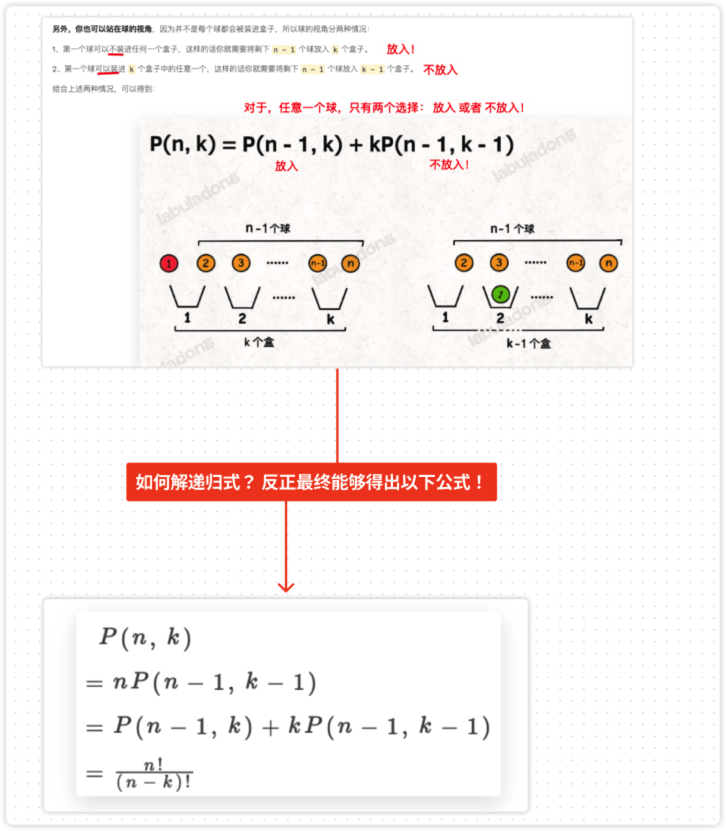
4. 该题分析

注意是
子序列
4.1. 暴力解法
一个思路是:
s 的子序列中有多少个 t , 所以找出所有的子序列即可,这是一个暴力解法
4.2. 拆解问题
考虑是否能够拆解成 规模更小的子问题 ,所以,更小的子问题是?
s[i..] 的子序列中 t[j..] 出现的次数为 dp(s, i, t, j)
所以,原题想要的结果是 dp(s, 0, t, 0) ,可写如下代码:

子序列是需要保证顺序的,所以是
s[i...]或者t[j...]
参考上面,请问:盒子多还是小球多?
t代表盒子s代表小球
所以,要做的事情就是把所有盒子都装上一个小球
5. 盒子的视角 , 即 t 的视角
dp(s, 0, t, 0) 如何转移呢?
- 以
s = "babgbag", t = "bag"为例:t[0]在s中的什么位置 ?s[0]和s[2]及s[4]- 所以
转化为:s[0...] , s[2...] , s[4...]中出现t[1...]的个数
上面的描述翻译成代码如下:

5.1. 最终可执行代码
/**
* @param {string} s
* @param {string} t
* @return {number}
*/
var numDistinct = function(s, t) {
// ::::dp(s, i, t, j) 表示 s[i..] 中 t[j..] 出现的个数
return dp(s, 0, t, 0);
};
function dp(s,i,t,j) {
//// :::: base case 1
if (j === t.length) {
// t 已经全部匹配完成
return 1;
}
// :::: base case 2
if (s.length - i < t.length - j) {
// s[i..] 比 t[j..] 还短,必然没有匹配的子序列
return 0;
}
// ::::代表出现的次数
let res = 0;
// :::: 在 s[i..] 中寻找 k,使得 s[k] == t[j]
for (let k = i; k < s.length; k++) {
if (s[k] === t[j]) {
// 累加结果
res += dp(s, k + 1, t, j + 1);
}
}
return res;
}
console.log(numDistinct('rabbbit', 'rabbit')); // 3
console.log(numDistinct('babgbag', 'bag')); // 5
5.2. 备忘录优化
/**
* @param {string} s
* @param {string} t
* @return {number}
*/
var numDistinct = function(s, t) {
// ::::add memo
const memo = new Array(s.length).fill([]);
for (let i = 0; i < s.length; i++) {
// :::: 为什么是 -1 ???因为储存的值是 出现次数
memo[i] = new Array(t.length).fill(-1);
}
return dp(s, 0, t, 0,memo);
};
function dp(s,i,t,j,memo) {
if (j === t.length) {
return 1;
}
if (s.length - i < t.length - j) {
return 0;
}
// :::: 查备忘录防止冗余计算
if (memo[i][j] !== -1) {
return memo[i][j];
}
let res = 0;
for (let k = i; k < s.length; k++) {
if (s[k] === t[j]) {
// 累加结果
res += dp(s, k + 1, t, j + 1,memo);
}
}
memo[i][j] = res;
return res;
}
console.log(numDistinct('rabbbit', 'rabbit'));// 3
console.log(numDistinct('babgbag', 'bag')); // 5
6. 算法复杂度分析
-
带备忘录的动态规划算法的时间复杂度
- =
子问题的个数*函数本身的时间复杂度 - =
「状态」的个数*函数本身的时间复杂度 - =
O(MN) * O(M) - =
O(N * M^2)
- =
M, N分别代表s, t的长度,算法的「状态」就是dp 函数参数i, j 的组合
7. 小球的视角 即 s 的视角
原问题是计算 s[0..] 的所有子序列中 t[0..] 出现的次数
s[0] = t[0],即能够匹配, 又有两种情况- 情况 1:去匹配:
=>s[1..]的所有子序列中计算t[1..]出现的次数 - 情况 2:不匹配:
=>s[1..]的所有子序列中计算t[0..]出现的次数
- 情况 1:去匹配:
s[0] != t[0]在s[1..]的子序列中计算t[0...]的出现次数
翻译成代码,即:
/**
* // ::::转态转移方程定义:
* s[i..] 的子序列中 t[j..] 出现的次数为 dp(s, i, t, j)
*/
var dp = function(s, i, t, j){
if(s[i] === t[j]){
// 匹配,两种情况,累加关系
// 1、去匹配 j+1
// 2、不去匹配 j
return dp(s, i + 1, t, j + 1) + dp(s, i + 1, t, j);
} else {
// 不匹配,在 s[i+1..] 的子序列中计算 t[j..] 的出现次数
return dp(s, i + 1, t, j);
}
}
为啥明明
s[0]可以匹配t[0],还不让它俩匹配呢?主要是为了给s[0]之后的元素匹配的机会
7.1. 带备忘录的解法
/**
* @param {string} s
* @param {string} t
* @return {number}
*/
var numDistinct = function(s, t) {
const memo = new Array(s.length).fill([]);
for (let i = 0; i < s.length; i++) {
memo[i] = new Array(t.length).fill(-1);
}
return dp(s, 0, t, 0, memo);
};
// 定义:s[i..] 的子序列中 t[j..] 出现的次数为 dp(s, i, t, j, memo)
var dp = function(s, i, t, j, memo) {
// base case 1
if (j === t.length) {
return 1;
}
// base case 2
if (s.length - i < t.length - j) {
return 0;
}
// 查备忘录防止冗余计算
if (memo[i][j] !== -1) {
return memo[i][j];
}
let res = 0;
// 执行状态转移方程
if (s[i] === t[j]) {
// 匹配,两种情况,累加关系
res += dp(s, i + 1, t, j + 1, memo) + dp(s, i + 1, t, j, memo);
} else {
// 不匹配,在 s[i+1..] 的子序列中计算 t[j..] 的出现次数
res += dp(s, i + 1, t, j, memo);
}
// 结果存入备忘录
memo[i][j] = res;
return res;
};
console.log(numDistinct('rabbbit', 'rabbit'));// 3
console.log(numDistinct('babgbag', 'bag')); // 5
7.2. 复杂度分析
-
带备忘录的动态规划算法的时间复杂度
- =
子问题的个数*函数本身的时间复杂度 - =
「状态」的个数*函数本身的时间复杂度 - =
O(MN) * O(1) - =
O(N * M)
- =
M, N分别代表s, t的长度,算法的「状态」就是dp 函数参数i, j 的组合
明显比性能更好
8. 总结
就算 dp 函数/数组的定义相同,如果你使用不同的「视角」进行穷举,效率也不见得是相同的
9. 思考
那么不妨进一步思考一下,什么样的动态规划题目可能产生「穷举视角」上的差异?换句话说,什么样的动态规划问题能够抽象成经典的「球盒模型」呢?