二叉树的分解问题思路

目录

• 1. 总结要点
• 3. 二叉树展开为链表
  • 3.1. ① 明确递归函数的定义，并相信它
  • 3.2. ② 明确 base case , 即 递归结束条件
  • 3.3. ③ 递归调用左右子树
  • 3.4. ④ 处理单链表指向问题
• 4. 附：刷题时的一个 约定
• 5. 杨辉三角 II
  • 5.1. 原题
  • 5.2. 动图
  • 5.3. 错误记录
  • 5.4. 代码
• 6. 杨辉三角
• 7. 二叉树的前后中序遍历：分解问题思路

1. 总结要点

• 原问题能不能分解为 规模更小，结构相同 的子问题
  • 如果能，就可以通过子问题的答案合并出原问题的答案
• 一定要明确递归函数的定义，并且需要相信 这个递归函数
  • base case 的两个主要判断依据，即递归结束的条件
    • ① 是不是空节点了，即 root === null
    • ② 是否到达了叶子节点 , 即 root.left === null && root.right === null
    • ③ 其他：根据题目情况而定
• 这里有不少题，不是二叉树，但这里旨在说明 递归的重要性

3. 二叉树展开为链表

3.1. ① 明确递归函数的定义，并相信它

/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
// ::::第一步：定义：输入一个二叉树，返回一个链表，它会打平
var flatten = function(root) {

};

• 如下图 ① 位置
  • root 传值给 flatten 函数，就会变成 下图中间位置那样
    • 至于，怎么变的，我不知道，但我相信这个flatten 函数
• 如下图 ② 位置：给子树调用完后 flatten 函数，需要处理 单链表 指向逻辑

3.2. ② 明确 base case , 即 递归结束条件

// ::::第一步：定义：输入一个二叉树，返回一个链表，它会打平
var flatten = function(root) {
    // ::::第二步：base case, 递归结束的条件
    if(root === null){
        return;
    }
    // ....
};

3.3. ③ 递归调用左右子树

/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
// ::::第一步：定义：输入一个二叉树，返回一个链表，它会打平
var flatten = function(root) {
    // ::::第二步：base case, 递归结束的条件
    if(root === null){
        return;
    }
    // ::::第三步：递归调用左右子树

    // ::::左子树已经被拉平成一条链表
    flatten(root.left);
    // :::: 让左子树指向变量 left，为了后面操作左右子树的指向，方便操作单链表
    let left = root.left;

    // ::::右子树已经被拉平成一条链表
    flatten(root.right);
    // :::: 让右子树指向变量 right，为了后面操作左右子树的指向，方便操作单链表
    let right = root.right;

};

3.4. ④ 处理单链表指向问题

/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
// ::::第一步：定义：输入一个二叉树，返回一个链表，它会打平
var flatten = function (root) {
    
    // ::::第二步：base case, 递归结束的条件
    if (root === null) {
        return;
    }
    // ::::第三步：递归调用左右子树

    // ::::左子树已经被拉平成一条链表
    flatten(root.left);
    // :::: 让左子树指向变量 left，为了后面操作左右子树的指向，方便操作单链表
    let left = root.left;

    // ::::右子树已经被拉平成一条链表
    flatten(root.right);
    // :::: 让右子树指向变量 right，为了后面操作左右子树的指向，方便操作单链表
    let right = root.right;

    /*************************************************
     * ::::处理单链表指向问题
     ************************************************/
    // ::::: ① 让左子树为空，右子树指向左子树
    root.left = null;
    root.right = left;

    // :::: ② 指针指向 p,一直前进，直到
    let p = root;
    while (p.right !== null) {
        p = p.right;
    }

    // :::: ③ 让右子树指向变量 right
    p.right = right;

};

三个重点：

• ① 相信这个 打平函数
• ② 调用左右子树后需要使用变量 left 和 right 去接受，方便后面处理单链表指向问题
• ③ 具体处理单链表指向问题，参考上图

4. 附：刷题时的一个 约定

一个技巧：

• **所有变量定义尽量都使用 let 省得后面还得改成 const

5. 杨辉三角 II

5.1. 原题

5.2. 动图

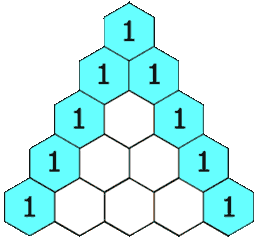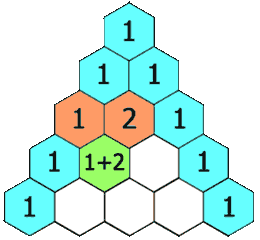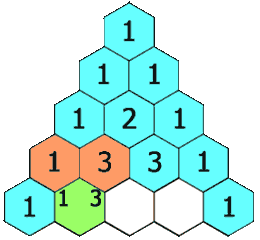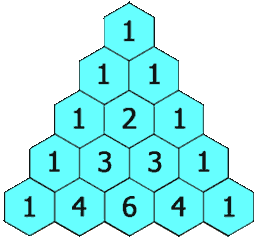
5.3. 错误记录

• 技巧：可以尝试运行，看看输出结果和实际结果，能够很快的判断错误原因，如下图：

5.4. 代码

/**
 * @param {number} rowIndex
 * @return {number[]}
 */
// ::::① 定义，返回第rowIndex行的数组，并且相信它
var getRow = function (rowIndex) {
    
    // ::::第一个元素是1
    let row = [1];
    
    // ::::② base case
    if (rowIndex === 0) {
        return row;
    }
    // ::::::③ 递归调用，新得到上一行的数组
    const preRow = getRow(rowIndex - 1);
    for (let i = 0; i < rowIndex - 1; i++) {
        const value = preRow[i] + preRow[i + 1];
        row.push(value)
    }
    // :::: 最后一个元素是1
    row.push(1);
    return row;
};

• 这题，不是二叉树问题，但旨在说明：相信递归函数的重要性

6. 杨辉三角

/**
 * @param {number} numRows
 * @return {number[][]}
 */
var generate = function (numRows) {
    // ::::base case
    let res = [];
    if (numRows < 1) {
        return res;
    }

    // ::::base case： 第一行
    let firstRow = [1];
    res.push(firstRow);

    // ::::// 开始一层一层生成，装入 res
    for (let i = 2; i <= numRows; i++) {
        let preRow = res[res.length - 1];
        res.push(generateNext(preRow));
    }

    return res;
};

/**
 * @description 生成下一行的数组
 * @param {Array} row 上一行的数组
 * */
var generateNext = function (row) {
    // ::::注意，是 [1] 不是 【0】，搞了半天
    const res = [1];
    for (let i = 0; i < row.length - 1; i++) {
        res.push(row[i] + row[i + 1]);
    }
    // ::::注意，是 [1] 不是 【0】，搞了半天
    res.push(1);
    return res;
}

• ① 这个题不是二叉树题目，刷到就随便刷了
• ② 关键是辅助函数的定义 generateNext ，一定要明确好这个函数的定义
• ③ 注意📢📢📢📢📢： 是[1]不是 [0]，搞了半天

7. 二叉树的前后中序遍历：分解问题思路

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function (root) {
    let res = [];

    // ::::base case
    if (root === null) {
        return res;
    }
    
    // ::::::前序位置
    res.push(root.val);
  
    res.push(...preorderTraversal(root.left));
  
    // ::::::::中序位置
  
    res.push(...preorderTraversal(root.right));
  
    // ::::::::后序位置

    return res;
};

① 这也解释了上图：为什么前后遍历，root 在第一个？因为对应代码位置！ ② 其他中序遍历和后序遍历 只需要改变一下顺序 ③ 简写，使用... ,注意格式：res.push(...preorderTraversal(root.right));

• 不是 res.push([...preorderTraversal(root.right)])