二叉树的两种解题思维

#算法/二叉树

两种 二叉树解题思维模式
应用：求二叉树的最大深度
应用：路径总和
- 解法一：遍历一遍二叉树 的思路
- 解法二：分解问题的思路
应用：翻转二叉树
- 解法一：通过 遍历一遍二叉树 的思路
- 解法二：使用分解问题的思路
应用：填充每个二叉树节点的右侧指针
- 解法一：遍历的思路
- 分解问题思路，没好的思路
应用：将二叉树展开为链表

`两种` 二叉树解题思维模式

「遍历」的思维模式
「分解问题」的思维模式

二叉树解题的思维模式 分两类

第一类：是否可以通过遍历一遍二叉树得到答案？
- 如果可以，用一个 traverse 函数配合外部变量来实现，这叫 「遍历」的思维模式。
**第二类：是否可以定义一个递归函数，通过子问题（子树）的答案 推导出 原问题的答案？
- 如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论使用哪种思维模式，你都需要思考：

如果单独抽出一个二叉树节点，

它需要做什么事情？
**需要在什么时候（前/中/后序位置）做？或者说 在哪个位置做？

其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

一定要相信这个递归函数 并且千万不要陷入递归函数

应用：求二叉树的最大深度

https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

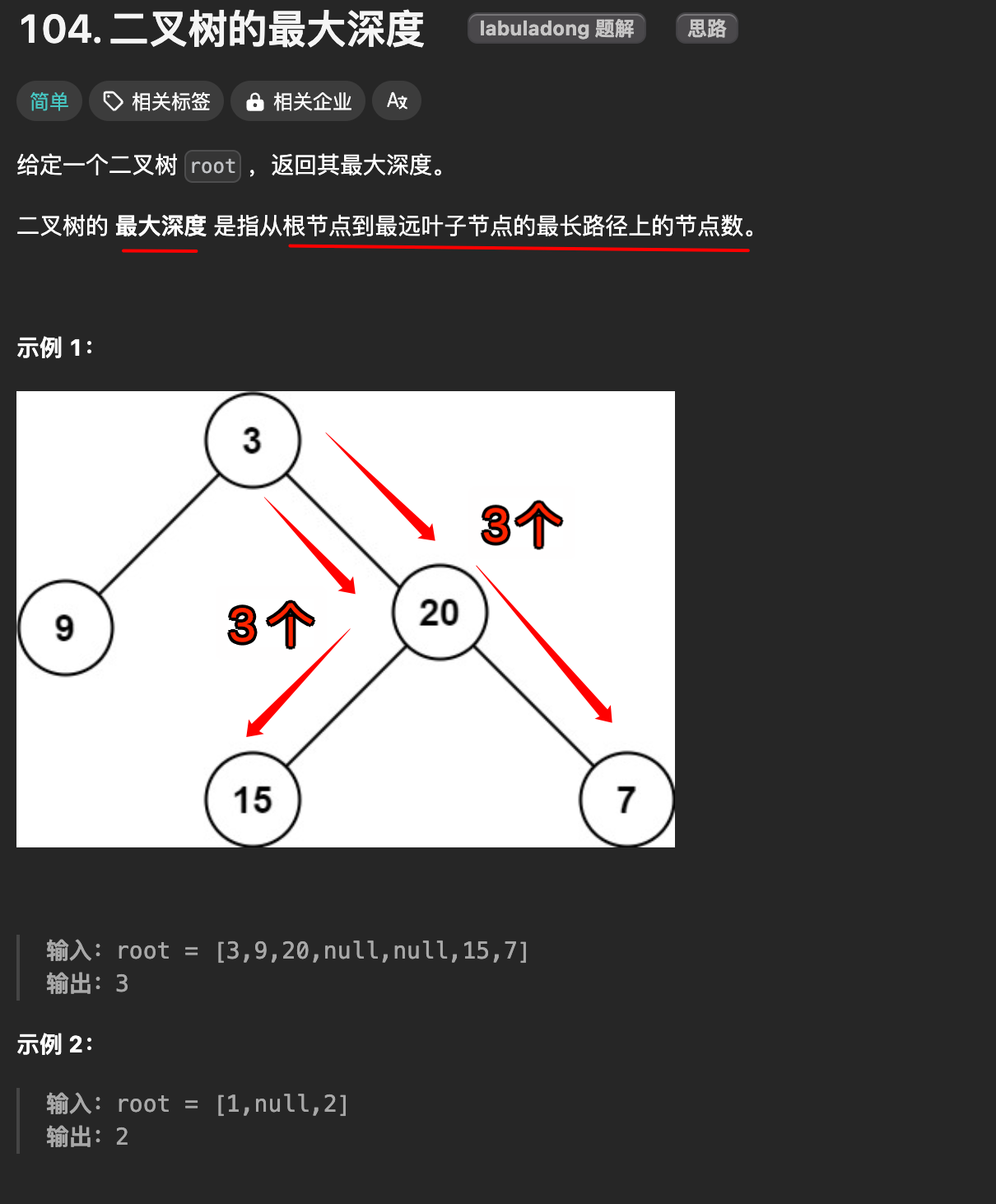
image.png|552

分析

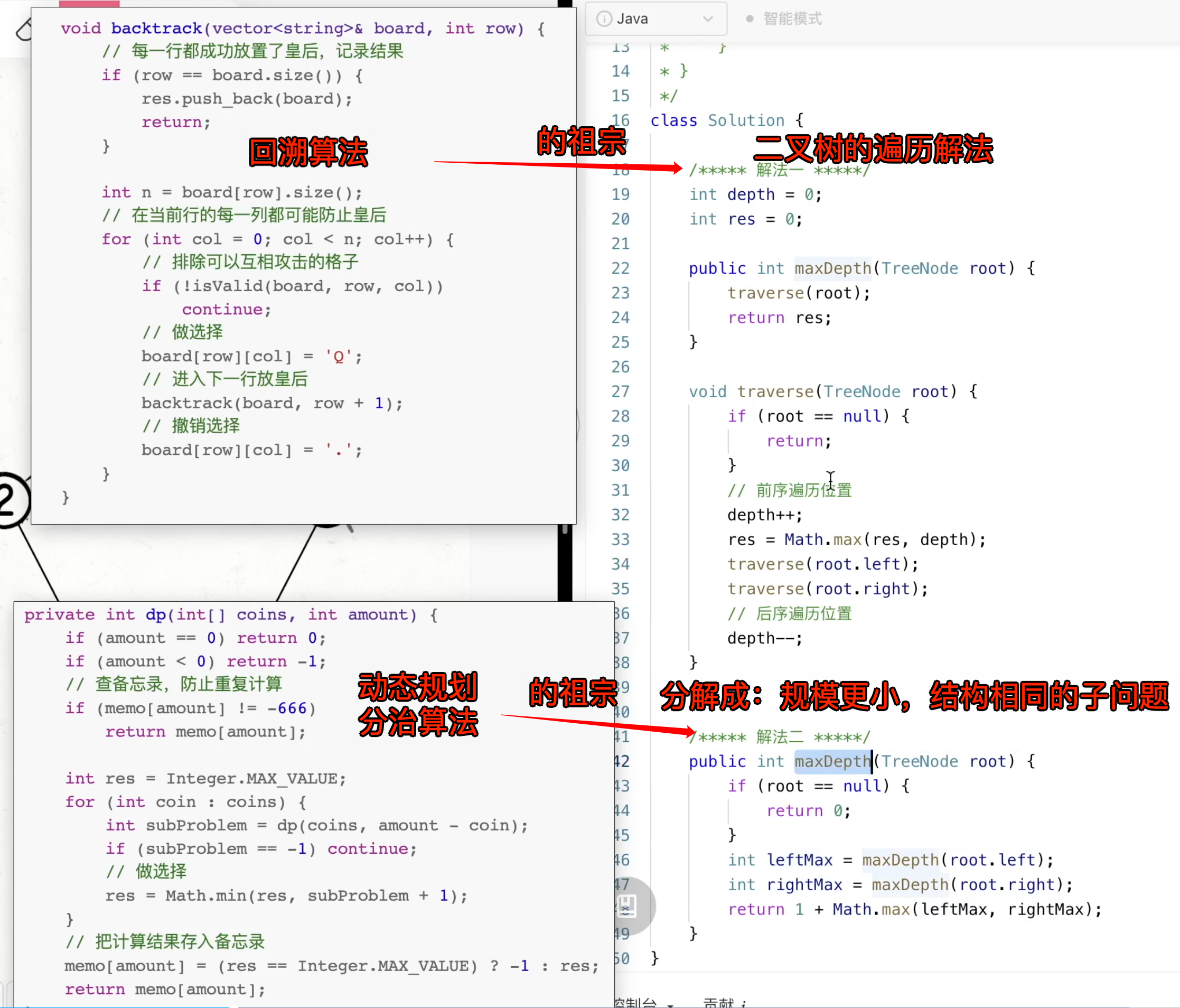
image.png|744

二叉树题目的递归解法可以分两类思路

第一类：遍历一遍二叉树得出答案

第二类：通过分解问题计算出答案这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。

`二叉树最大深度`的两种思路

遍历的思路
- 它是 回溯算法的祖宗
分解问题的思路
- 它是 动态规划 和 分治算法 的 祖宗
- 分解成 规模更小，结构相同 的子问题

解法一：`遍历一遍二叉树`的思路

/**
 * :::: 解法一：遍历一遍二叉树
 * @param {TreeNode} root
 * @return {number}
 * https://leetcode.cn/problems/maximum-depth-of-binary-tree/
 */
var maxDepth = function (root) {
    let res = 0;

    // ::::需要正确的维护深度，即前序遍历++ 后序遍历--
    let depth = 0;

    function traverse(root) {
        // ::::base case
        if (root === null) return res;
        // ::::前序位置
        depth++;

        // ::::如果到达叶子节点，更新res
        if (root.left === null && root.right === null) {
            res = Math.max(res, depth);
        }

        traverse(root.left);
        // :::::中序位置
        traverse(root.right);
        // ::::后序位置
        depth--;
    }

    traverse(root);

    return res;
};

traverse 理解成在二叉树上游走的一个指针，所以当然要这样维护 depth

res 的更新，前后中序都行

解法二：`分解问题为左右子树` 的思路

/**
 * :::: 解法二：分解问题的思路
 * @param {TreeNode} root
 * @return {number}
 * @url https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
 */
var maxDepth = function (root) {
    // ::::base case
    if (root === null) return 0;

    // ::::前序位置
    
    // ::::分解问题, 分别求左右子树的最大深度
    const left = maxDepth(root.left);
    
    // ::::中序位置
    const right = maxDepth(root.right);

    // ::::后序位置，合并结果，为什么要在后序位置合并结果呢？
    // ::::因为要先解决子问题，即计算出左右子树的最大深度，才能推导出父类的最大深度
    
    // ::::合并结果
    return Math.max(left, right) + 1;

};

问：为什么主要的代码逻辑集中在后序位置？

见代码注释

应用：路径总和

image.png|608

解法一：`遍历一遍二叉树` 的思路

/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function (root, targetSum) {
    let hasSum = false;
    let sum = 0;
    function traverse(root) {
        // ::::base case
        if (root === null) return;
        // ::::前序位置
        sum += root.val;
        // ::::如果到达叶子节点，判断是否满足条件
        if (root.left === null && root.right === null) {
            if (sum === targetSum) {
                hasSum = true;
            }
        }
        traverse(root.left);
        // ::::中序位置
        traverse(root.right);
        // ::::后序位置
        sum -= root.val;
    }
    traverse(root);
    return hasSum;
};

这里可以优化，只要找到了，存在了，就没必要继续遍历了

**需要在 前序和后续位置 维护 sum 变量

解法二：`分解问题`的思路

/**
 * @url https://leetcode.cn/problems/path-sum/description/
 * */
/**
 * @description 路径总和,分解成左右子树的问题
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function(root, targetSum) {
  
    // ::::base case
    if (root === null) return false;

    // ::::前序位置

    // ::::如果到达叶子节点，判断是否满足条件
    // ::::都到达叶子节点了，说明没有左右子树了，这时候只需要判断当前节点的值是否等于 targetSum 即可
    if (root.left === null && root.right === null) {
        return targetSum === root.val;
    }

    // ::::分解问题, 分别求左右子树中是否存在路径和为 targetSum - root.val
    const hasPathInleft = hasPathSum(root.left, targetSum - root.val);

    // ::::中序位置
    const hasPathInRight = hasPathSum(root.right, targetSum - root.val);

    // ::::后序位置
    // ::::？？？为什么要在后序位置合并结果呢？
    return hasPathInleft || hasPathInRight;

};

应用：翻转二叉树

image.png|448

解法一：通过 `遍历一遍二叉树` 的思路

/**
 * @description 翻转二叉树,遍历一遍二叉树的解决方案
 * @param {TreeNode} root
 * @return {TreeNode}
 */
// ::::::解法一：通过遍历一遍二叉树得到结果
var invertTree = function(root) {

    function traverse(root) {
        // ::::base case
        if(root === null){
            return;
        }

        // ::::交换左右子树
        // ::::问：为什么在前序位置处理逻辑呢？
        const temp = root.left;
        root.left= root.right;
        root.right = temp;

        // ::::前序位置
        traverse(root.left);
        // :::: 中序位置
        traverse(root.right);
        // ::::后序位置
      
    }

    traverse(root);

    // ::::原地修改
    return root;
};

**可使用 前序遍历、后序遍历、及层次遍历，但不能使用中序遍历 为什么不能使用 中序遍历 如下解释：

解法二：使用`分解问题`的思路

// ::::分解问题的思路
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
    // ::::base case 这是递归的基本情况，也是递归结束的标志
    // 基本情况：如果当前节点为空，直接返回null
    if (root === null) {
        return null;
    }

    // ::::前序位置
    // :::: 对于非空节点，我们递归地调用invertTree函数来翻转当前节点的左子树和右子树。
    // :::: 这里的关键在于，我们先保存左子树翻转的结果，再翻转右子树，然后将两者交换。
    //  :::: 即使用 left 和 right 来个变量来保存左右子树的翻转结果
    // :::: 这样做是因为在递归调用过程中，原来的左右子树已经被修改，所以需要先保存它们的结果
    // 分解问题：递归地翻转左子树和右子树
    let left = invertTree(root.left);
    let right = invertTree(root.right);
    // ::::后序位置
    // 将翻转后的左子树和右子树交换
    root.left = right;
    root.right = left;

    // 返回翻转后的根节点
    return root;
};

问：为什么在后序位置 处理主要逻辑？ 很明显，这个时候才能拿到翻转过的 left 和 right 啊

应用：填充每个二叉树节点的右侧指针

image.png|536

输入是一棵「完美二叉树」，形象地说整棵二叉树是一个正三角形

除了最右侧的节点 next 指针会指向 null
其他节点的右侧一定有相邻的节点

解法一：遍历的思路

// 二叉树遍历函数
void traverse(Node root) {
    if (root == null || root.left == null) {
        return;
    }
    // 把左子节点的 next 指针指向右子节点
    root.left.next = root.right;

    traverse(root.left);
    traverse(root.right);
}

上面代码有问题，5和6不属于同一节点，没法串起来。

image.png|560

所以，我们得想想如何遍历两个相邻节点之间的空隙

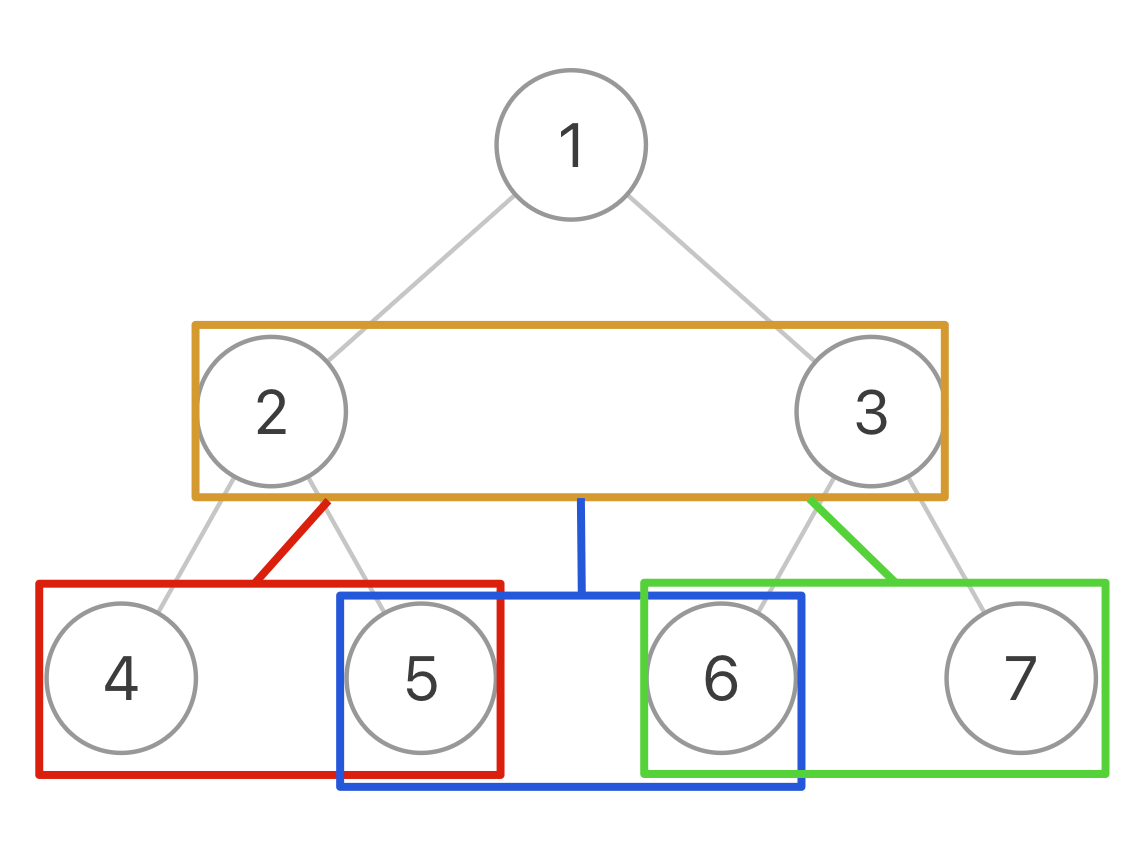
image.png|544

这样，一棵二叉树被抽象成了一棵三叉树，三叉树上的每个节点就是原先二叉树的两个相邻节点。

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function(root) {
    if(root === null){
        return null;
    }
    // 遍历「三叉树」，连接相邻节点
    traverse(root.left,root.right);
    return root;
};


// 三叉树遍历框架
function traverse(node1,  node2) {
    if (node1 == null || node2 == null) {
        return;
    }
    /**** 前序位置 ****/
    // 将传入的两个节点穿起来
    node1.next = node2;
    // 连接相同父节点的两个子节点
    traverse(node1.left, node1.right);
    traverse(node2.left, node2.right);
    // 连接跨越父节点的两个子节点
    traverse(node1.right, node2.left);
}

传入多少个参数，很重要，同步重要，比如和上面的传入的两个参数

拿出一个点来，自己画画，分析下就好了

分解问题思路，没好的思路

省略

应用：将二叉树展开为链表

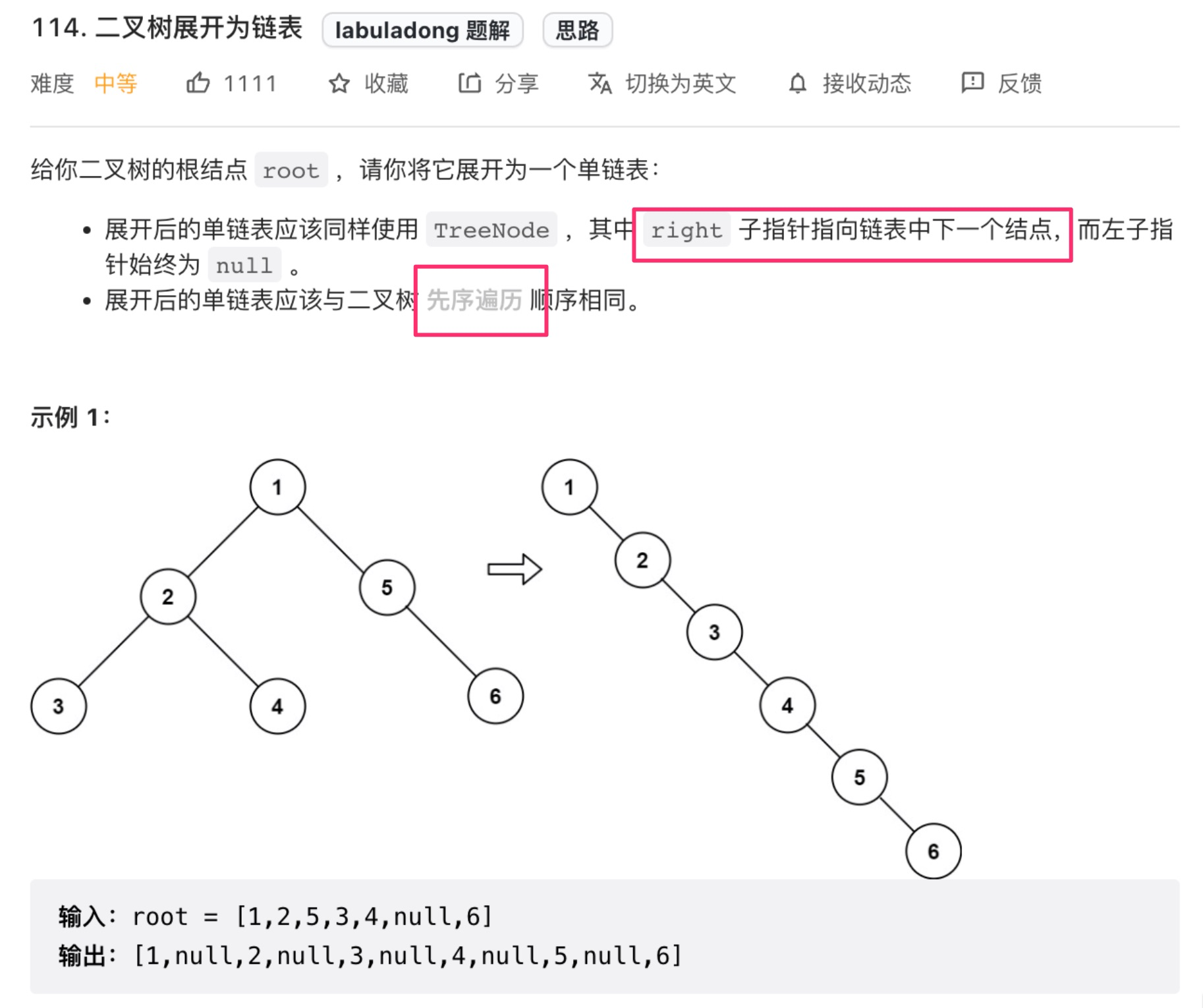
image.png|648

遍历的思路

省略

分解问题

对于一个节点 x，可以执行以下流程：

先利用 flatten(x.left) 和 flatten(x.right) 将 x 的左右子树拉平。
后序遍历位置，将 x 的 右子树接到左子树下方，然后将整个左子树作为右子树。

image.png|584

递归的魅力就在于，不容易说清楚，也别尝试完全理解它，差不多就行了，但只是让每个节点做他应该做的事情，然后就搞定了。


/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
    // base case
    // 因为是原点操作，return就好
    if(root === null){
        return;
    }

    // 利用定义，把左右子树拉平
    flatten(root.left);
    flatten(root.right);

    /**** 后序遍历位置 ****/
    // 1、这时，左右子树已经被拉平成一条链表，先保存这时候的左右子树状态
    let left = root.left;
    let right = root.right;


    // 2、将左子树作为右子树
    root.left = null;
    root.right = left;


    // 3、将原先的右子树接到当前右子树的末端
    // (1) 先要遍历已有right节点，同链表
    // (2) 将最早保存的right节点指到最后
    let p = root;
    while (p.right != null) {
        p = p.right;
    }
    p.right = right;
};

总结

**二叉树问题的两种思维模式
- **「遍历」的思维模式
- 「分解问题」的思维模式
- **无论哪种模式，都需要思考对每个节点需要做什么，在哪做（前中序）
**两种思维模式，对应着两种框架
- 回溯算法框架
- 动态规划&分治问题框架
一定要相信这个递归函数，不要陷入递归函数

liguwe's site