矩阵置零

#leetcode #2024/08/26 #算法 #算法/矩阵

1. 总结
- 1.1.1. 思路一：简单
- 1.2. 思路二：原矩阵中利用==第一行和第一列==记录状态，避免了额外的空间消耗
2. 题目及理解
3. 解题思路
4. 代码实现
5. 复杂度分析
6. 问题记录
- 6.1. 使用原矩阵的第一行和第一列来记录状态不会污染原有数据吗？

1. 总结

1.1.1. 思路一：简单

第一次遍历，记录0的位置，记得使用==集合==
第二次遍历，置零

function setZeroes(matrix) {
  const rows = new Set();
  const cols = new Set();
  const m = matrix.length;
  const n = matrix[0].length;
  // 第一次遍历，记录0的位置
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (matrix[i][j] === 0) {
        rows.add(i);
        cols.add(j);
      }
    }
  }
  // 第二次遍历，置零
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (rows.has(i) || cols.has(j)) {
        matrix[i][j] = 0;
      }
    }
  }
}

1.2. 思路二：原矩阵中利用==第一行和第一列==记录状态，避免了额外的空间消耗

2. 题目及理解

原题： https://leetcode.cn/problems/set-matrix-zeroes/

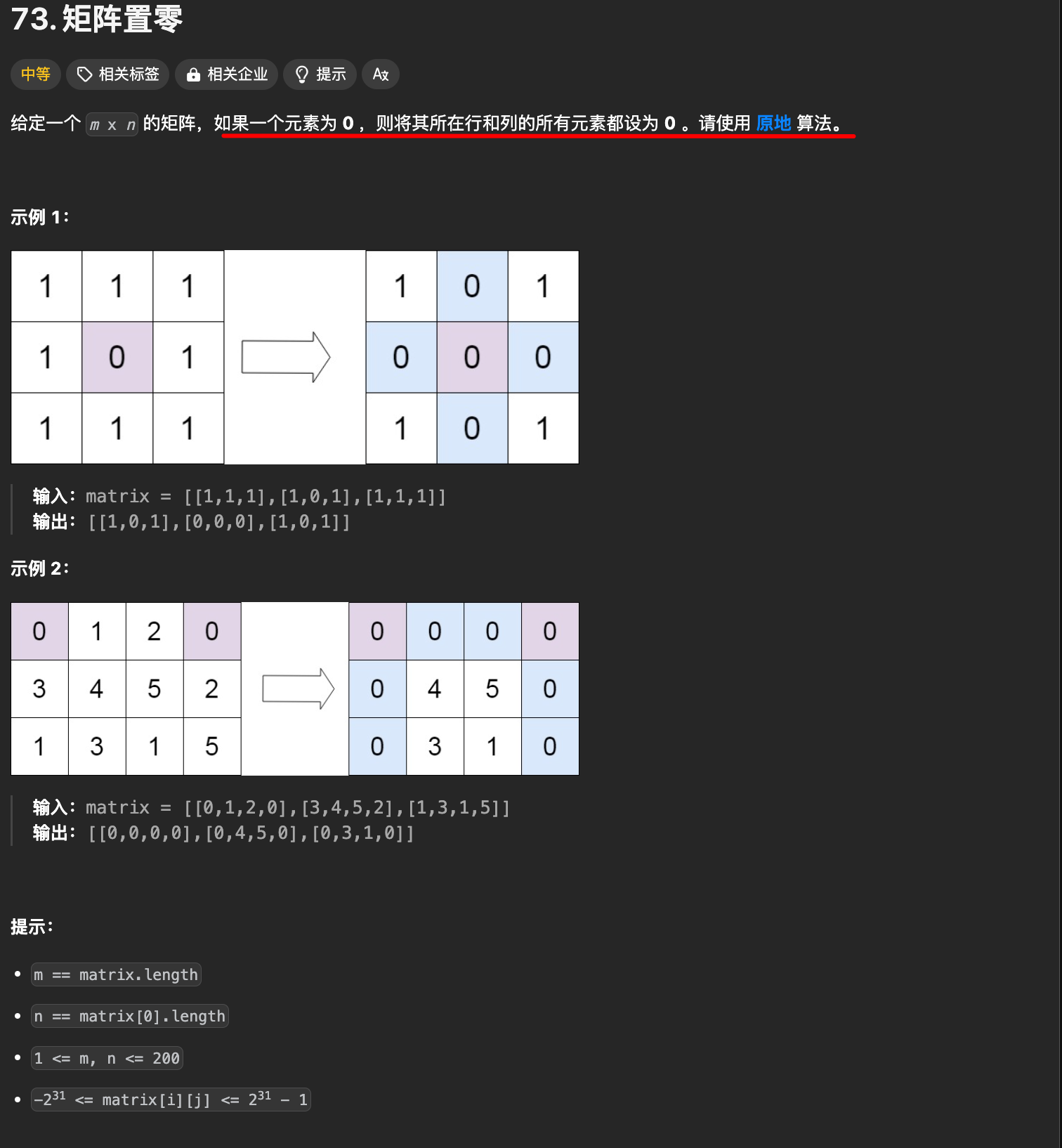
cos-blog-832-34-20241012|928

题意好理解，读一遍就知道了

3. 解题思路

使用原矩阵的第一行和第一列来记录是否需要置为 0，具体思路如下：

标记第一行和第一列
- 首先检查第一行和第一列是否有零，并用两个布尔变量 firstRowZero 和 firstColZero 记录下来。
使用第一行和第一列作为标记
- 从第二行和第二列开始遍历矩阵
  - 如果遇到零，就在对应的第一行和第一列的位置上标记为零
根据标记置零
- 再次遍历矩阵（从第二行和第二列开始）
- 根据第一行和第一列的标记，如果是 0，则将对应的元素置零
处理第一行和第一列
- 根据 firstRowZero 和 firstColZero 的值，决定是否将第一行和第一列置零。

这种方法通过在原矩阵中利用第一行和第一列记录状态，避免了额外的空间消耗，符合题目要求的原地修改。

4. 代码实现

/**  
 * @param {number[][]} matrix  
 * @return {void} Do not return anything, modify matrix in-place instead.  
 */var setZeroes = function(matrix) {  
    const m = matrix.length;  
    const n = matrix[0].length;  
    let firstRowHasZero = false;  
    let firstColHasZero = false;  
    /*************************************************  
     * ::::① 首先检查第一行和第一列是否有零，
     * 并用两个布尔变量`firstRowZero`和`firstColZero`记录下来  
     ************************************************/  
    // 检测第一行是否有 0 ，记得 break    for (let j = 0; j < n; j++) {  
        if (matrix[0][j] === 0) {  
            firstRowHasZero = true;  
            break;  
        }  
    }  
    // 检测第一列是否有 0 ，记得 break    for (let i = 0; i < m; i++) {  
        if (matrix[i][0] === 0) {  
            firstColHasZero = true;  
            break;  
        }  
    }  
    /*************************************************  
     * :::::② 遍历除第一行和第一列以外的所有元素，
     * 如果有零则将对应的第一行和第一列的元素置零  
     ************************************************/  
    for (let i = 1; i < m; i++) {  
        for (let j = 1; j < n; j++) {  
            if (matrix[i][j] === 0) {  
            // 将第一行和第一列作为标志位, 标记该行或该列是否需要清零  
            // 如果 matrix[i][j] === 0, 则将 matrix[i][0] 和 matrix[0][j] 置为 0               // 即将该行和该列的第一个元素置为 0，标记该行和该列需要清零  
                matrix[i][0] = matrix[0][j] = 0;  
            }  
        }  
    }  
    /*************************************************  
     * ::::::③ 根据第一行和第一列的标志位对矩阵的其余元素进行清零  
     ************************************************/  
    // 从第二行第二列开始遍历，如果 matrix[i][0] === 0 或 matrix[0][j] === 0，  
    // 则将 matrix[i][j] 置为 0    
    for (let i = 1; i < m; i++) {  
        for (let j = 1; j < n; j++) {  
            if (matrix[i][0] === 0 || matrix[0][j] === 0) {  
                matrix[i][j] = 0;  
            }  
        }  
    }  
    /*************************************************  
     * ::::::④ 根据第一个元素标记的第一行和第一列是否需要清零  
     ************************************************/  
    // 如果第一行需要清零  
    if (firstRowHasZero) {  
        for (let j = 0; j < n; j++) {  
            matrix[0][j] = 0;  
        }  
    }  
    // 如果第一列需要清零  
    if (firstColHasZero) {  
        for (let i = 0; i < m; i++) {  
            matrix[i][0] = 0;  
        }  
    }  
};

5. 复杂度分析

时间复杂度是 O(m*n)，
空间复杂度是 O(1)，符合题目要求的原地算法

6. 问题记录

6.1. 使用原矩阵的第一行和第一列来记录状态不会污染原有数据吗？

使用原矩阵的第一行和第一列来记录状态不会污染原有数据，因为：

提前记录状态：在标记之前，先用两个布尔变量 firstRowZero 和 firstColZero 记录第一行和第一列是否有零。
从第二行和第二列开始标记
- 只从第二行和第二列开始使用标记，避免影响第一行和第一列的原始状态。
- 虽然标记的是第一行或第一列，但是如果这一行或者这一列已经有 0，那么最终第一行（或列）最终还得是 0
最后处理第一行和第一列：根据之前记录的布尔变量，最后再决定是否将第一行和第一列置零。

这样可以安全地使用第一行和第一列来存储标记信息，而不影响最终结果。

liguwe's site