二维数组的遍历技巧

#2023/05/27 #算法 #done

目录

• 1. 总结
• 2. 重要性
• 3. 如何初始化一个二维数组
  • 3.1. 关于 Array.fill 的用法
• 4. 第 48 题「 旋转图像」
  • 4.1. 关键思路
  • 4.2. 延伸：逆时针呢？
    • 4.2.1. 问题 1： 这里为什么是 j < n-i ?
    • 4.2.2. 问题 2：问题 2 ： 为什么是 matrix[n - j - 1][n - i - 1] ？
• 5. 第 151 题「 颠倒字符串中的单词」
  • 5.1. 原地反转所有单词的顺序
  • 5.2. 错误日志
  • 5.3. 复杂度分析
  • 5.4. 那么js 版本的原地算法呢？
• 6. 第 54 题「 螺旋矩阵」
• 7. 第 59 题「 螺旋矩阵 II」
• 8. 最后总结

1. 总结

• 如何初始化一个二维数组：
  • 两次 new Array(len)
    • 两次 fill ，一定要使用 map
      • new Array(n).fill(new Array(n).fill(0));
        • 这种写法有问题，每行==引用同一个数组==
• ==顺时针==旋转 n*n 二维数组
  • ① 先按==正对角线==反转
    • 作为正：即 ==↘==
  • ② 再按==列反转==即可
  • ==要点==：
    • 临时变量 temp
    • 直接 使用 Array.reverse
      • 或者使用双指针直接实现，记得使用 while
• ==逆时针==旋转 n*n 二维数组
  • ① 先按==反对角线==反转，即 ==↗==
    • ==这个相对复杂些，自己实现一个看看==
      • ==一定要画图，就知道如何遍历了==
  • ② 再按 ==列== 反转
• 颠倒字符串中的单词（原地反转所有单词的顺序）
  • ① 先反转==整个字符串==
  • ② 然后再反转 ==每个单词==
• ==顺时针螺旋==遍历二维数组：m*n
  • 关键点：
    • 四个变量：上下左右
    • while (res.length < m * n) {
      • ==4 个 if==：
        • 顶部：从左向右，顶部需要 if( top <= bottom )
          • for 遍历，里面都是 <= 或者 >=
          • top ++
  • 注意点：==画图看图==
• 生成螺旋矩阵： 1 → n^2 顺时针组成的二维数组
  • 第一步：初始化
    • res：二维数组 res，初始值都为 0
    • 四个变量：上下左右边界
    • cur = 1 ： 1 ~ n^2
  • 第二步：
    • 然后==顺时针螺旋遍历==这个二维数组
      • while (cur <= n*n)
    • 同时，把 cur 赋值给当前遍历到的元素
      • 然后 cur ++
  • ==大量复用顺时针螺旋遍历的代码，再多几个变量而已==

文本编辑器下 length 经常写错，请注意

2. 重要性

• 动态规划 经常需要 遍历二维 dp 数组
• 二维遍历，既考验编程能力，也考验一些技巧性思路

3. 如何初始化一个二维数组

let arr = new Array(3).fill(new Array(5).fill("*"));

两次 new Array

3.1. 关于 Array.fill 的用法

fill(value)
fill(value, start)
fill(value, start, end)

比如：
console.log([1, 2, 3].fill()); // [undefined, undefined, undefined]

const array1 = [1, 2, 3, 4];

// Fill with 0 from position 2 until position 4
console.log(array1.fill(0, 2, 4));
// Expected output: Array [1, 2, 0, 0]

// Fill with 5 from position 1
console.log(array1.fill(5, 1));
// Expected output: Array [1, 5, 5, 5]

console.log(array1.fill(6));
// Expected output: Array [6, 6, 6, 6]

4. 第 48 题「 旋转图像」

https://leetcode.cn/problems/rotate-image/

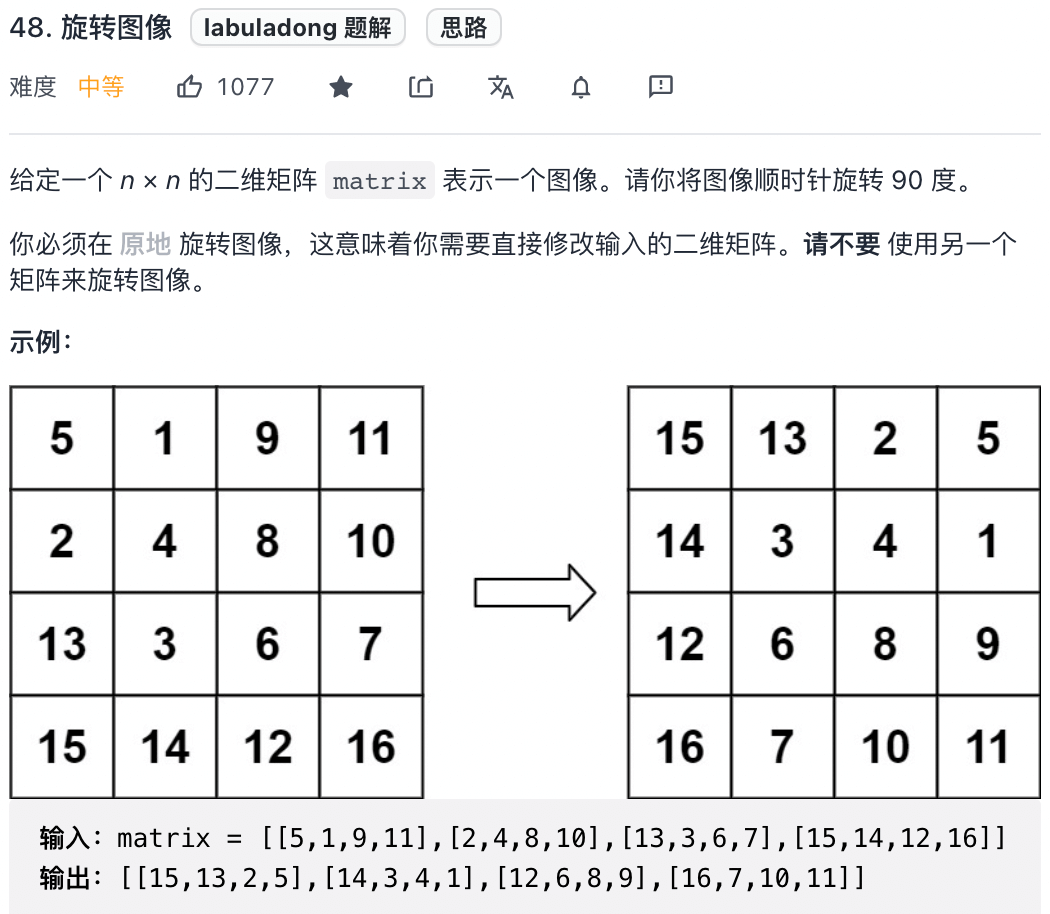
这里要求原地，参考 #原地反转所有单词的顺序 , 所以，这里常规思路搞不定，得换一种思路，如下图：

https://www.figma.com/file/hT9k2YbVvV1UIITtUmbJ0C/2023.05.LOG?type=whiteboard&node-id=147-180&t=sZSmw8G9XgtflSer-4

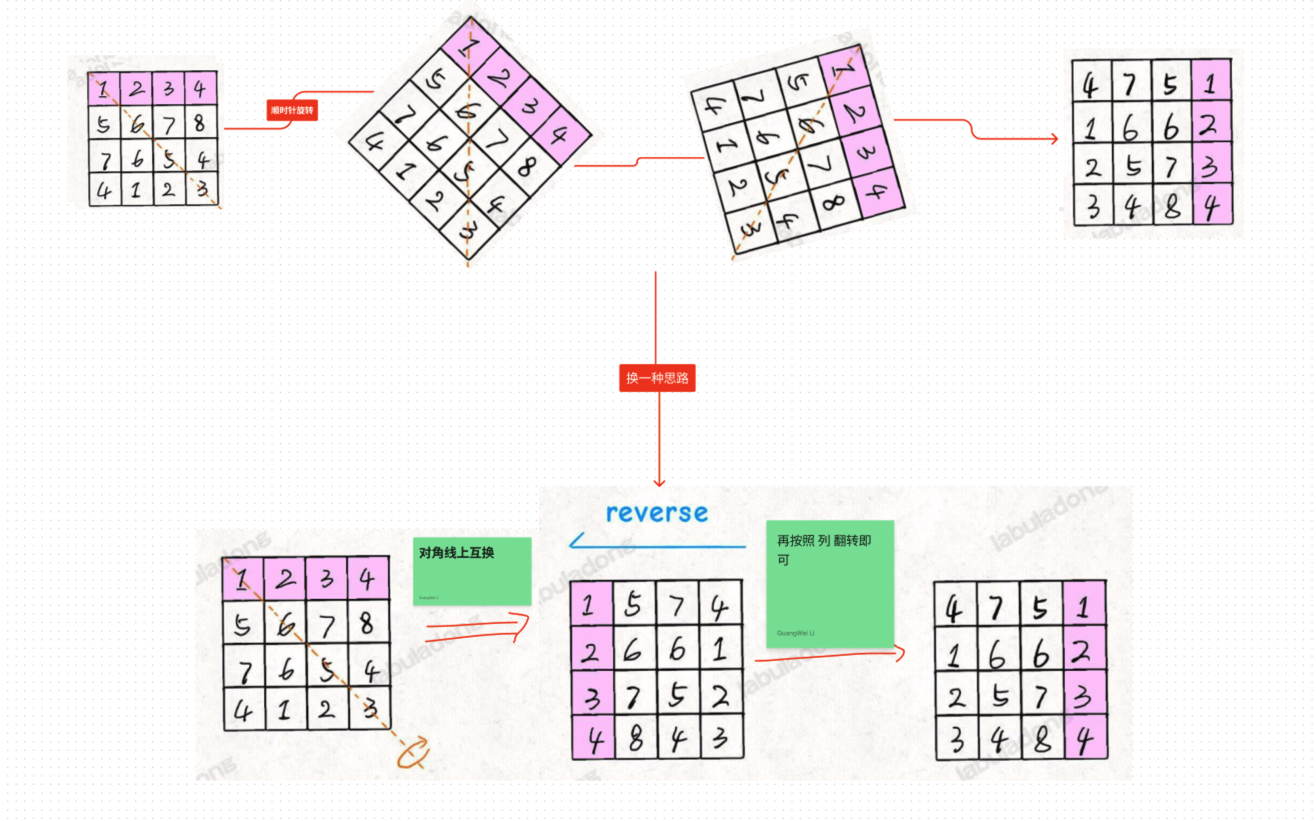
4.1. 关键思路

• ① 先按==正对角线==反转
• ② 再按==列反转==即可

let rotate = function (matrix) {
    let n = matrix.length;
    // 先沿【对角线】镜像对称二维矩阵
    // :::: 交换 matrix[i][j] 和 matrix[j][i]
    for (let i = 0; i < n; i++) {
        // ::::这里 j=i，遍历第 i 行后，只需要交换对称线右上方的元素即可
        //  如果 j 从 0 开始，会把对称线左下方的元素也交换了，即相当于根本就没有交互
        for (let j = i ; j < n; j++) {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
    // 然后反转二维矩阵的【每一行】
    for (let row of matrix) {
        reverse(row);
        // 或者 
        // row.reverse()
    }
}

/**
 * 同样使用双指针技巧实现数组的翻转
 * */
let reverse = function (arr) {
    let i = 0,
        j = arr.length - 1;
    while (j > i) {
        let temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
        i++;
        j--;
    }
}


let matrix = [1, 2, 3], [4, 5, 6], [7, 8, 9](/post/nyKWO1Wx.html#1,-2,-3],-[4,-5,-6],-[7,-8,-9);
let matrix2 = [5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16](/post/nyKWO1Wx.html#5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16)
// 原地修改两个数组
rotate(matrix);
rotate(matrix2);
console.log(matrix);
console.log(matrix2);

[!question] 注意点：为什么交换 matrix[i][j] 和 matrix[j][i] 时，内层循环 从 j = i 开始？

上面的问题可以见代码注释部分，另外这里补充下，其实只需要遍历矩阵的右上角的节点即可，如下图：

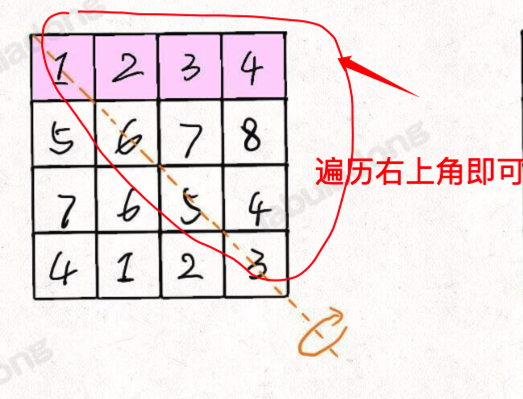
4.2. 延伸：逆时针呢？

同理，分为两步骤，如下图：

• 【对角线】如下图进行旋转
• 按 每行进行翻转即可

所以根据上面的代码，修改如下即可：

let rotate = function (matrix) {
    let n = matrix.length;
    // 先沿【对角线】镜像对称二维矩阵
    for (let i = 0; i < n; i++) {
        //   问题 1： 这里为什么是 j < n-i  ?
        //   问题 2 ： 为什么是 matrix[n - j - 1][n - i - 1] ？ 
        for (let j = 0; j < n - i; j++) {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[n - j - 1][n - i - 1];
            matrix[n - j - 1][n - i - 1] = temp;
        }
    }

    // 然后反转二维矩阵的【每一行】
    for (let row of matrix) {
        reverse(row);
    }
}

/**
 * 同样使用双指针技巧实现数组的翻转
 * */
let reverse = function (arr) {
    let i = 0,
        j = arr.length - 1;
    while (j > i) {
        let temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
        i++;
        j--;
    }
}

let matrix = [1, 2, 3], [4, 5, 6], [7, 8, 9](/post/nyKWO1Wx.html#1,-2,-3],-[4,-5,-6],-[7,-8,-9);
let matrix2 = [5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16](/post/nyKWO1Wx.html#5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16)
// 原地修改两个数组
rotate(matrix);
rotate(matrix2);
console.log(matrix);
console.log(matrix2);

4.2.1. 问题 1： 这里为什么是 j < n-i ?

同理，主需要遍历左上方的元素即可，如下图

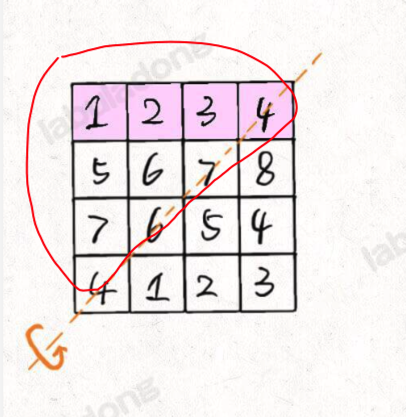
4.2.2. 问题 2：问题 2 ： 为什么是 matrix[n - j - 1][n - i - 1] ？

以 i = 0 j = 1 为例， 这里 2 = matrix[0][1] 对应着 最下方 4 即位置 matrix[2][3] ，即 matrix[n - j - 1][n - i - 1] ，如下图：

5. 第 151 题「 颠倒字符串中的单词」

https://leetcode.cn/problems/reverse-words-in-a-string/submissions/ https://leetcode.cn/problems/fan-zhuan-dan-ci-shun-xu-lcof/

5.1. 原地反转所有单词的顺序

s = "hello world labuladong"
// 你的算法需要原地反转这个字符串中的单词顺序,如下：
s = "labuladong world hello"

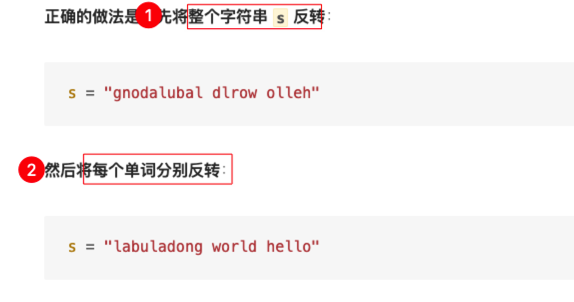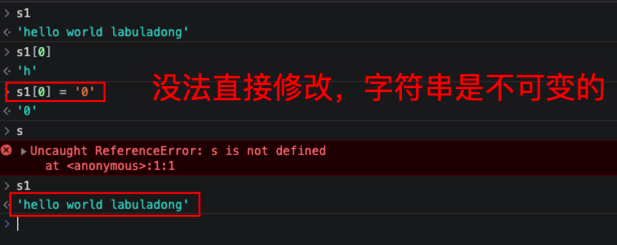
常规的做法肯定搞不定，比如 split(‘ ’) 成数组，然后 reverse 后再 join, 它使用了额外的空间，非原地 , 正确的思路如下： 是否能够实现原地，主要的差别是有些语言的字符串不可变（如 Java 和 Python、JavaScript )，有些语言的字符串可变（如 C++) ，如下图： 所以，还是需要借助额外的空间，以下是其中一种解法，当然它不是原地的

let s1 = "hello   world    labuladong  ";

/**
 * 去除多余空格
 * */
function removeSpace(s1) {
    return s1.trim().replace(/\s+/g,' ');
}

/**
 * 使用双指针技巧实现字符串的翻转
 * */
function reverseString(str) {
    let left = 0;  // 左指针
    let right = str.length - 1;  // 右指针
    let arr = removeSpace(str).split('');  // 将字符串转换为字符数组
    while (left < right) {
        // 交换左右指针指向的字符
        const temp = arr[left];
        arr[left] = arr[right];
        arr[right] = temp;
        // 移动指针
        left++;
        right--;
    }
    return arr.join('');  // 将字符数组转换回字符串
}
console.log(reverseString(s1)); // gnodulab dlrow olleh


/**
 * @param {string} s
 * @return {string}
 */
var reverseWords = function(s) {
    const newStr = reverseString(s);
    const arr = newStr.split(' ');
    const res = [];
    for (let i = 0; i < arr.length; i++) {
        res.push(reverseString(arr[i]));
    }
    return res.join(' ');
};

console.log(reverseWords(s1)); // labuladong world hello

5.2. 错误日志

因为高亮了吧，正则竟然加了一个''

5.3. 复杂度分析

5.4. 那么js 版本的原地算法呢？

TODO

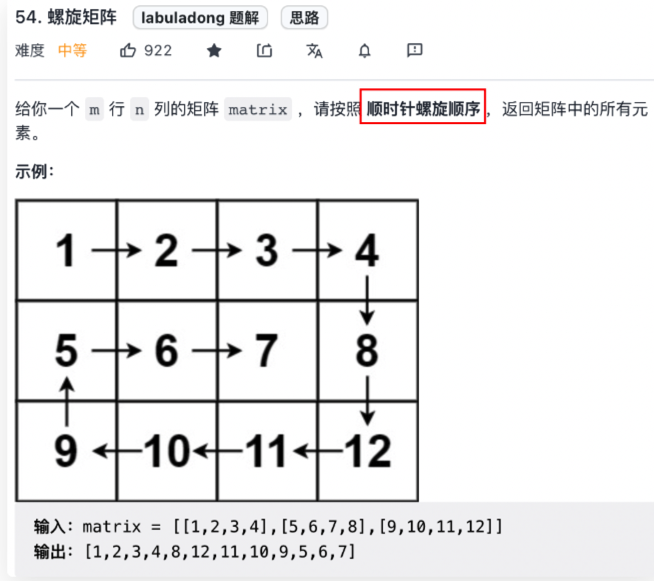
6. 第 54 题「 螺旋矩阵」

https://leetcode.cn/problems/spiral-matrix/ 注意：本题与主站 54 题相同： https://leetcode-cn.com/problems/spiral-matrix/

分析，如fj https://www.figma.com/file/hT9k2YbVvV1UIITtUmbJ0C/2023.05.LOG?type=whiteboard&node-id=151-215&t=ONxyxYCCotSe5XMX-4

[!info] 上图中，其实按照序号及图示遍历即可，每个变量应该如何遍历，是 ++ 还是 -- ，上图中都有标注，所以把上面的思路翻译成代码即可

以下是==代码==部分：

let spiralOrder = function (matrix) {
    let m = matrix.length, n = matrix[0].length;
    let top = 0, bottom = m - 1;
    let left = 0, right = n - 1;
    let res = [];
    // res.length == m * n 则遍历完整个数组
    while (res.length < m * n) {
        if (top <= bottom) {
            // 在顶部从左向右遍历
            for (let j = left; j <= right; j++) {
                res.push(matrix[top][j]);
            }
            // 上边界下移
            top++;
        }
        if (left <= right) {
            // 在右侧从上向下遍历
            for (let i = top; i <= bottom; i++) {
                res.push(matrix[i][right]);
            }
            // 右边界左移
            right--;
        }
        if (top <= bottom) {
            // 在底部从右向左遍历
            for (let j = right; j >= left; j--) {
                res.push(matrix[bottom][j]);
            }
            // 下边界上移
            bottom--;
        }
        if (left <= right) {
            // 在左侧从下向上遍历
            for (let i = bottom; i >= top; i--) {
                res.push(matrix[i][left]);
            }
            // 左边界右移
            left++;
        }
    }
    return res;
};

7. 第 59 题「 螺旋矩阵 II」

https://leetcode.cn/problems/spiral-matrix/submissions/

8. 最后总结

• 注意如何初始化一个二维数组，常用两种方式
• 无论顺时针还是逆时针，按对角线旋转一个二维数组，两个步骤
  • 记得按对角线 交换元素
  • 然后按照列翻转
• 顺时针或逆时针 打印二维数组，记得画图，更新四个变量即可