二叉搜索树的特性

#BST #leetcode #二叉树/二叉搜索树

目录

• 2. 二叉搜索树中第K小的元素
  • 2.1. 题意
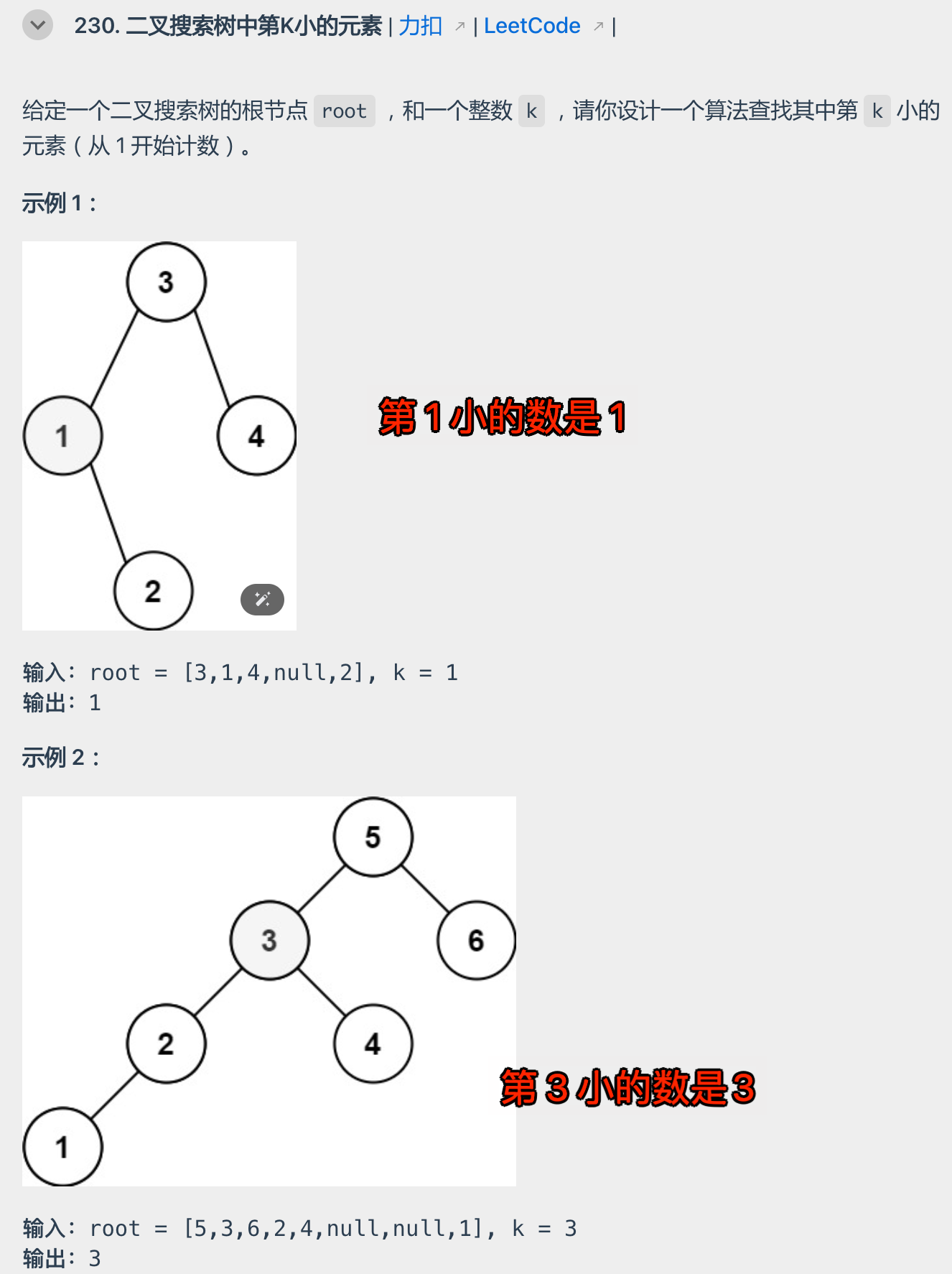
  • 2.2. 代码实现
  • 2.3. 复杂度分析
  • 2.4. 优化：中序遍历 + 数组缓存
• 3. 把二叉搜索树转换为累加树
  • 3.1. 题目
  • 3.2. 注意点
• 4. 参考
• 5. 相关题目

2. 二叉搜索树中第K小的元素

2.1. 题意

2.2. 代码实现

var kthSmallest = function (root, k) {
  let res = 0;
  function traverse(node) {
    if (!node) return;

    traverse(node.left);
    /*********************************
     ********** 中序位置 **************
     **********************************/
    k--;
    // k === 0 时，表示已经找到第 k 小的元素
    if (k === 0) {
      res = node.val;
      return;
    }
    traverse(node.right);
  }

  traverse(root);

  return res;
};

2.3. 复杂度分析

时间复杂度：

1. 最佳情况：O(k)
   • 如果第 k 小的元素在树的左侧较浅的位置，我们可能只需要访问 k 个节点就能找到它。
2. 最坏情况：O(n)
   • 如果 k 等于节点总数，或者第 k 小的元素在树的右侧较深的位置，我们可能需要遍历整棵树。
   • n 是树中节点的总数。
3. 平均情况：O(n)
   • 在平均情况下，我们可能需要遍历大部分节点才能找到第 k 小的元素。

空间复杂度：O(h)，其中 h 是树的高度

1. 主要的空间消耗来自于递归调用栈。
2. 在最坏情况下（树完全不平衡，呈现为一条链），高度 h 可能等于节点数 n，此时空间复杂度为 O(n)。
3. 在最佳情况下（完全平衡二叉树），高度 h 约等于 log(n)，此时空间复杂度为 O(log n)。

额外说明：

• 这个解法没有使用任何额外的数据结构来存储节点，这有助于保持较低的空间复杂度。
• 虽然我们定义了几个变量（count, result），但它们占用的空间是常数级的，不随输入规模变化，因此在分析空间复杂度时可以忽略不计。

总结：

• 时间复杂度：
  • 最佳 O(k)
  • 最坏和平均 O(n)
• 空间复杂度：O(h)，其中 h 是树的高度，最坏情况下可能达到 O(n)

这个解法在时间和空间效率上都是相当不错的，特别是对于平衡的二叉搜索树，它的性能表现会更好。

2.4. 优化：中序遍历 + 数组缓存

这种方法适用于树不经常变动，但频繁查询不同 k 值的情况

3. 把二叉搜索树转换为累加树

3.1. 题目

/**
 * @description 二叉搜索树转累加树
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var convertBST = function (root) {
  var sum = 0;

  var traverse = function (root) {
    if (root == null) {
      return;
    }
    // 需要反序中序遍历
    // 先进入右子树，再访问根节点，最后左子树
    // 所以中序遍历的逆序是：右 -> 根 -> 左
    // 计算累加和时，需要先遍历右子树，再累加根节点的值，最后遍历左子树
    traverse(root.right);
    /*****************
     * 中序遍历位置
     ****************/
    // 维护累加和
    sum += root.val;
    // 将 BST 转化成累加树
    root.val = sum;
    traverse(root.left);
  };

  traverse(root);

  // 返回根节点
  return root;
};

3.2. 注意点

• 需要先遍历右节点 ， 这样在中序位置的代码就是 右 → 根节点 → 左
  • sum = 所有右节点 + 根节点的值

4. 参考

https://labuladong.online/algo/data-structure/bst-part1/

5. 相关题目