二叉搜索树:Python 描述
#BST #数据结构
目录
- 1. 总结
- 2. 二叉搜索树(BST)
- 3. 二叉树效率:都是 O(n)
- 4. 二叉树的查找:复杂度 O(logn)
- 5. BST 的遍历:中序遍历升序
- 6. 插入节点:复杂度 O(logn)
- 7. 移除节点
- 8. BST 的使用场景
1. 总结
- 左小右大
- 因为这个特性,它可以提供
logN级别的增删查改效率 - 直接基于 BST 的数据结构有 ==AVL 树,红黑树==等
- 因为这个特性,它可以提供
- 它的==每个子节点==的左侧子树和右侧子树都是 BST
- BST 的中序遍历结果是升序的
2. 二叉搜索树(BST)
- 一种特殊的二叉树,
较小的值保存在左节点中,较大的值保存在右节点中根节点的左子树都比根节点的值小,右子树的值都比根节点的值大。二叉查找树是一种有序的树,所以支持快速查找、快速插入、删除一个数据
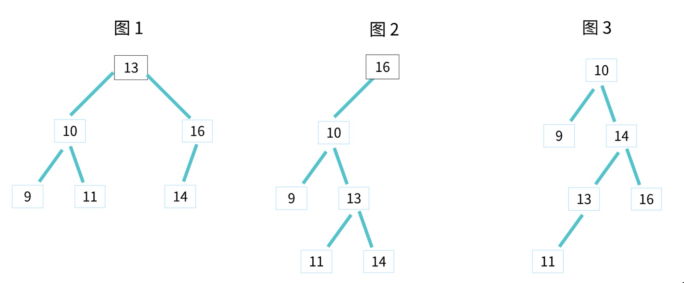
3. 二叉树效率:都是 O(n)
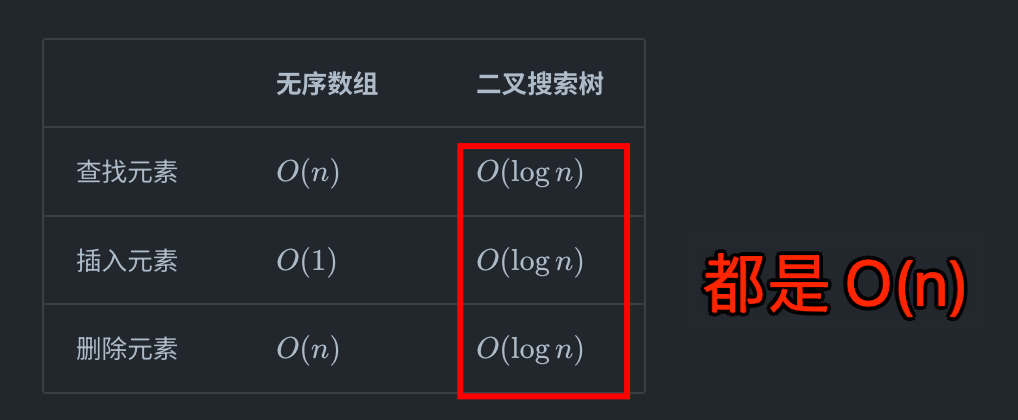
4. 二叉树的查找:复杂度 O(logn)
# BST的搜索
class TreeNode:
def __init__(self, val):
self.val = val
self.left:TreeNode | None = None
self.right:TreeNode | None = None
# BST的搜索
def search(root:TreeNode, val:int) -> TreeNode | None:
# 如果根节点为空,返回空
if root is None:
return None
# 如果根节点的值等于 val,返回根节点
if root.val == val:
return root
# 如果根节点的值大于 val,递归搜索左子树
if root.val > val:
if root.left is None:
return None
return search(root.left, val)
# 如果根节点的值小于 val,递归搜索右子树
if root.val < val:
if root.right is None:
return None
return search(root.right, val)
5. BST 的遍历:中序遍历升序
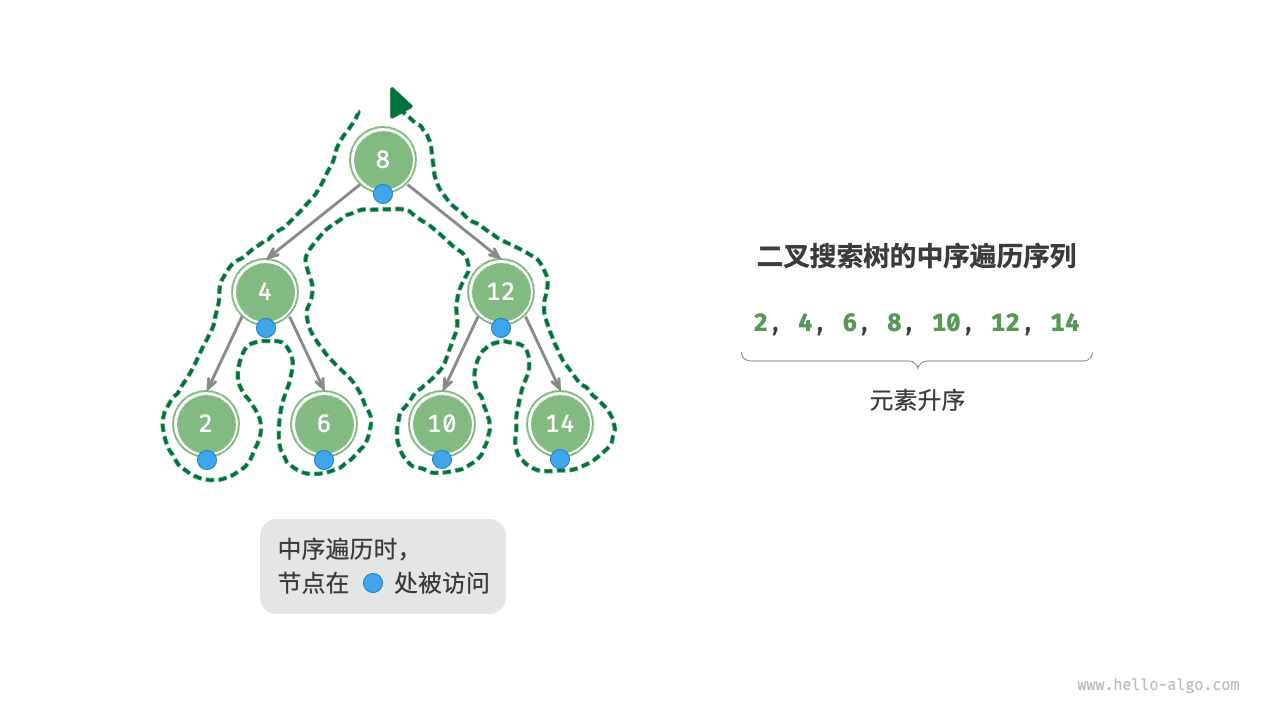
6. 插入节点:复杂度 O(logn)
[!danger] 二叉搜索树不允许存在重复节点,否则将违反其定义
因为BST的特性,所以插入的节点肯定会到叶子结点
- 查找插入位置
- 与查找操作相似,从根节点出发,根据当前节点值和
num的大小关系循环向下搜索,直到越过叶节点(遍历至None)时跳出循环。
- 与查找操作相似,从根节点出发,根据当前节点值和
- 在该位置插入节点
- 初始化节点
num,将该节点置于None的位置
- 初始化节点
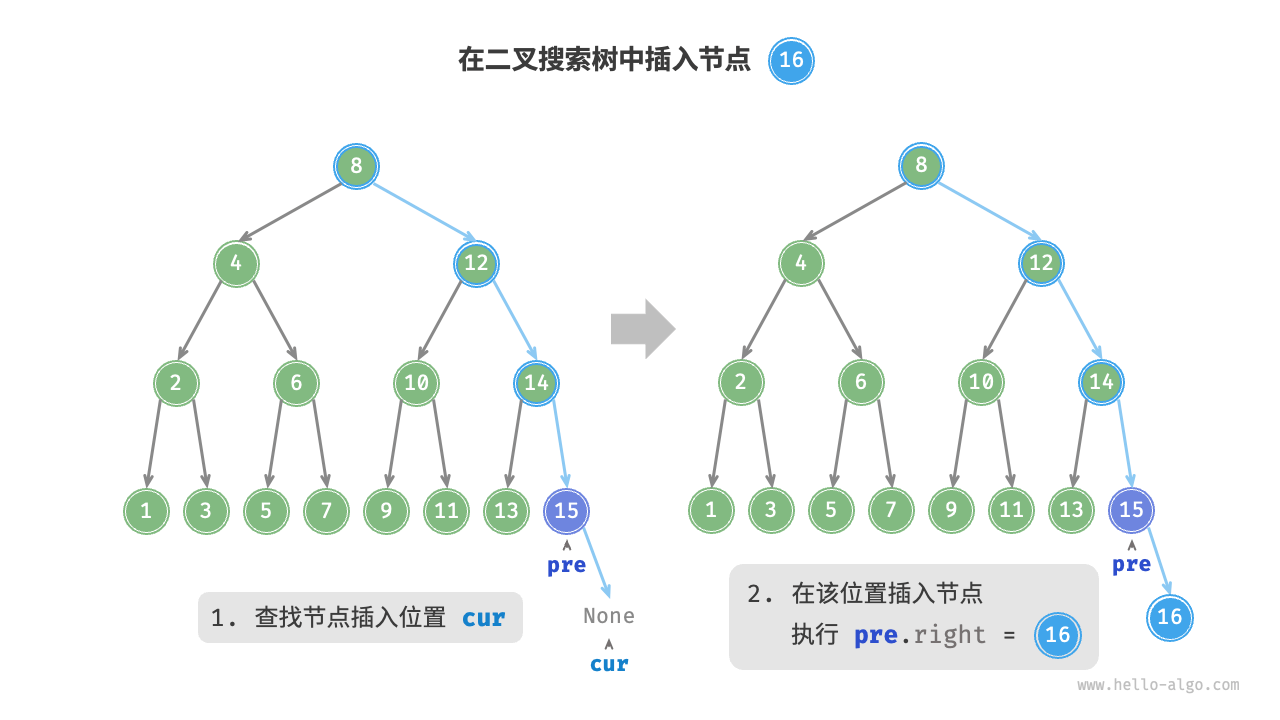
或者看下面一张图,在下图的树中插入健值为 6 的节点,一定是叶子节点对吧
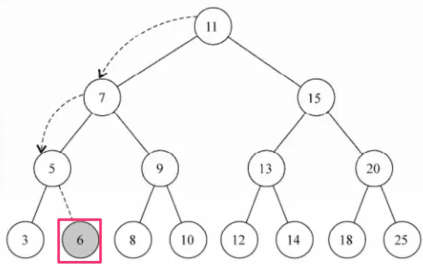
代码:
# TreeNode 类型的定义
class TreeNode:
def __init__(self, val):
self.val = val
self.left:TreeNode | None = None
self.right:TreeNode | None = None
# BST的插入,复杂度 O(logn)
def insert(root:TreeNode, val:int) -> TreeNode:
# 如果根节点为空,返回一个新节点
if root is None:
return TreeNode(val)
# 如果根节点的值大于 val,递归插入左子树
if root.val > val:
if root.left is None:
root.left = TreeNode(val)
root.left = insert(root.left, val)
# 如果根节点的值小于 val,递归插入右子树
if root.val < val:
if root.right is None:
root.right = TreeNode(val)
root.right = insert(root.right, val)
return root
7. 移除节点
7.1. 第一种情况:叶子结点
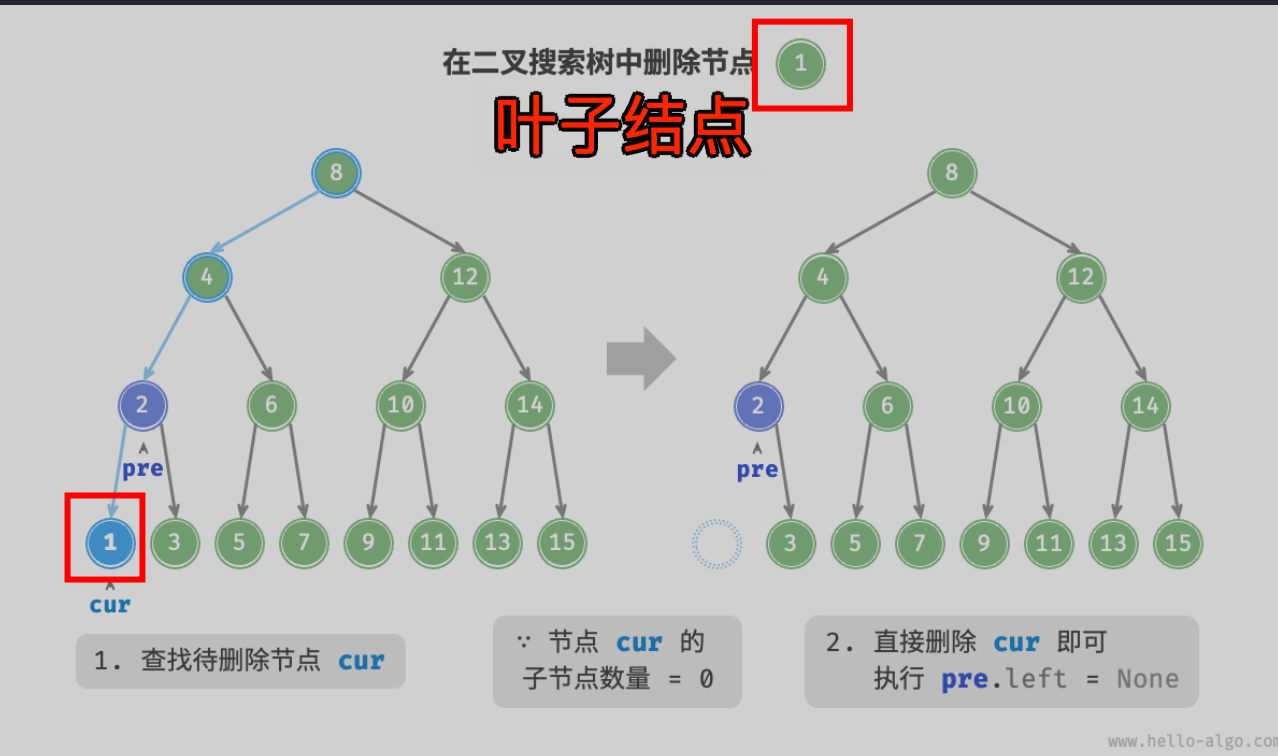
7.2. 第二种情况:有一个节点
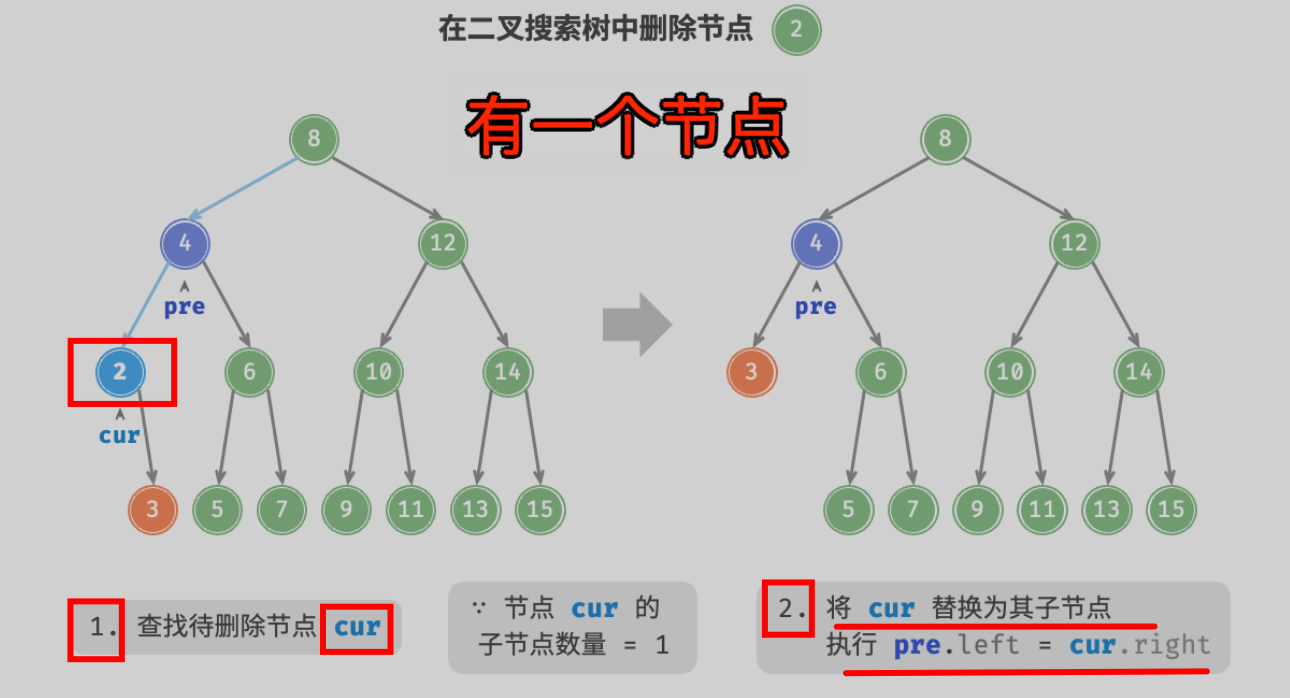
7.3. 第三种情况:两个子节点的节点
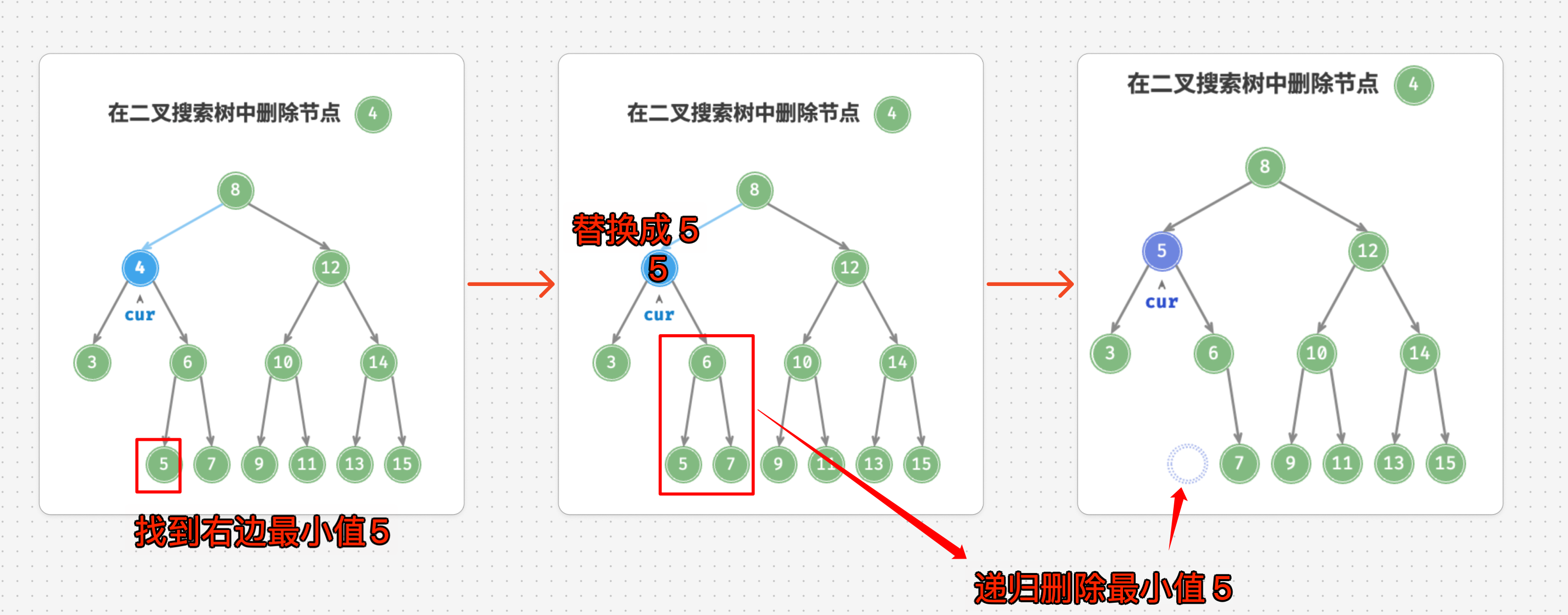
- 找到
4 - 找到
4的右边最小的节点5 - 把
4 的位置替换成5 - 递归从从右侧子树中移除最小节点
- 这个最小值一定是 5,并且是满足第一种情况:是叶子结点
7.4. 最终代码
# TreeNode 类型的定义
class TreeNode:
def __init__(self, val):
self.val = val
self.left:TreeNode | None = None
self.right:TreeNode | None = None
# BST的删除
def deleteNode(root:TreeNode, key:int) -> TreeNode | None:
# 如果根节点为空,直接返回
if root is None:
return None
# 如果根节点的值等于 key
if root.val == key:
"""第一种情况:叶子结点直接删除"""
# 如果左右孩子都为空,直接删除
if root.left is None and root.right is None:
return None
"""第二种情况:左孩子或者右孩子为空"""
# 如果左孩子为空,返回右孩子
if root.left is None:
return root.right
# 如果右孩子为空,返回左孩子
if root.right is None:
return root.left
"""走到这里说明是第三种情况:左右孩子都不为空"""
# 如果左右孩子都不为空
# 找到右子树的最小值
minNode = getMin(root.right)
# 将 root 的值替换为 minNode 的值
root.val = minNode.val
# 删除 minNode
root.right = deleteNode(root.right, minNode.val)
# 如果根节点的值小于 key
elif root.val < key:
if root.right is None:
return root
# 递归删除右子树
root.right = deleteNode(root.right, key)
# 如果根节点的值大于 key
else:
if root.left is None:
return root
# 递归删除左子树
root.left = deleteNode(root.left, key)
# 返回根节点
return root
# 找到最小值
def getMin(node:TreeNode) -> TreeNode:
# 找到最左边的节点,因为最左边的节点是最小的
while node.left is not None:
node = node.left
return node
8. BST 的使用场景
- 用作系统中的多级索引,实现高效的查找、插入、删除操作。
- 作为某些搜索算法的底层数据结构。
- 用于存储数据流,以保持其有序状态。