最小路径和
#算法/动态规划
目录
总结
- 思路
- 定义 :
dp[i][j]从 grid[0][0] 走到 grid[i][j] 的最小路径和
- base case
- 尽量使用迭代解法,解出来的大概率都能通过用例
- 定义 :
代码:迭代解法
/**
* @param {number[][]} grid
* @return {number}
*/
var minPathSum = function (grid) {
let m = grid.length;
let n = grid[0].length;
let dp = new Array(m).fill().map(() => {
return new Array(n).fill(-1);
});
// dp[i][j] 从 grid[0][0] 走到 grid[i][j] 的最小路径和
dp[0][0] = grid[0][0];
for (let j = 1; j < n; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (let i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
dp[i][j] = Math.min(
dp[i - 1][j] + grid[i][j],
dp[i][j - 1] + grid[i][j]);
}
}
return dp[m - 1][n - 1];
};
错误记录
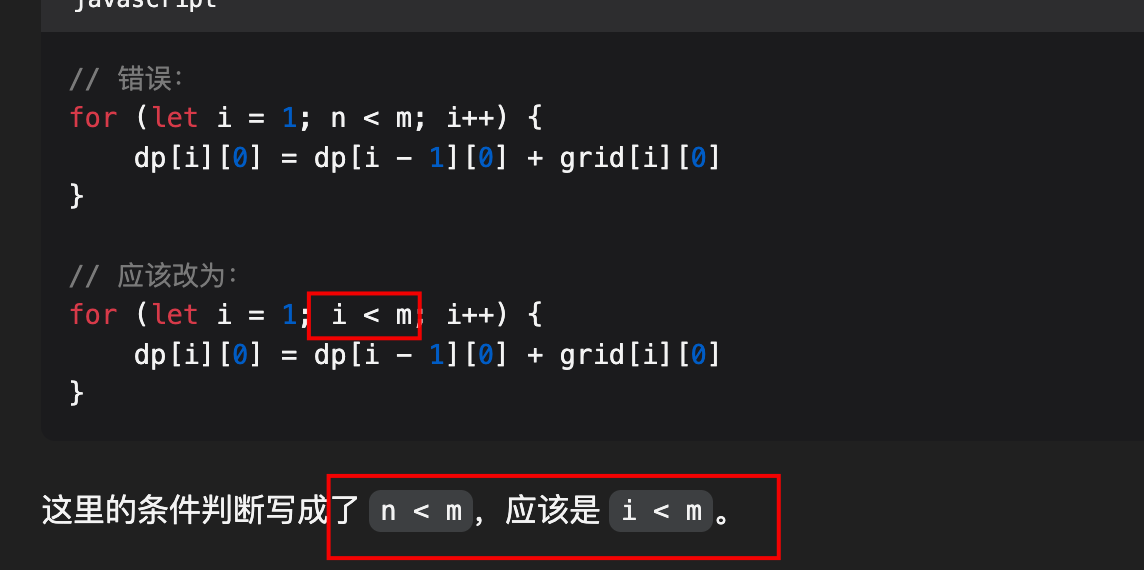
找了半天,人眼睛还是不容易发现,AI 一下就发现了
1. 题目
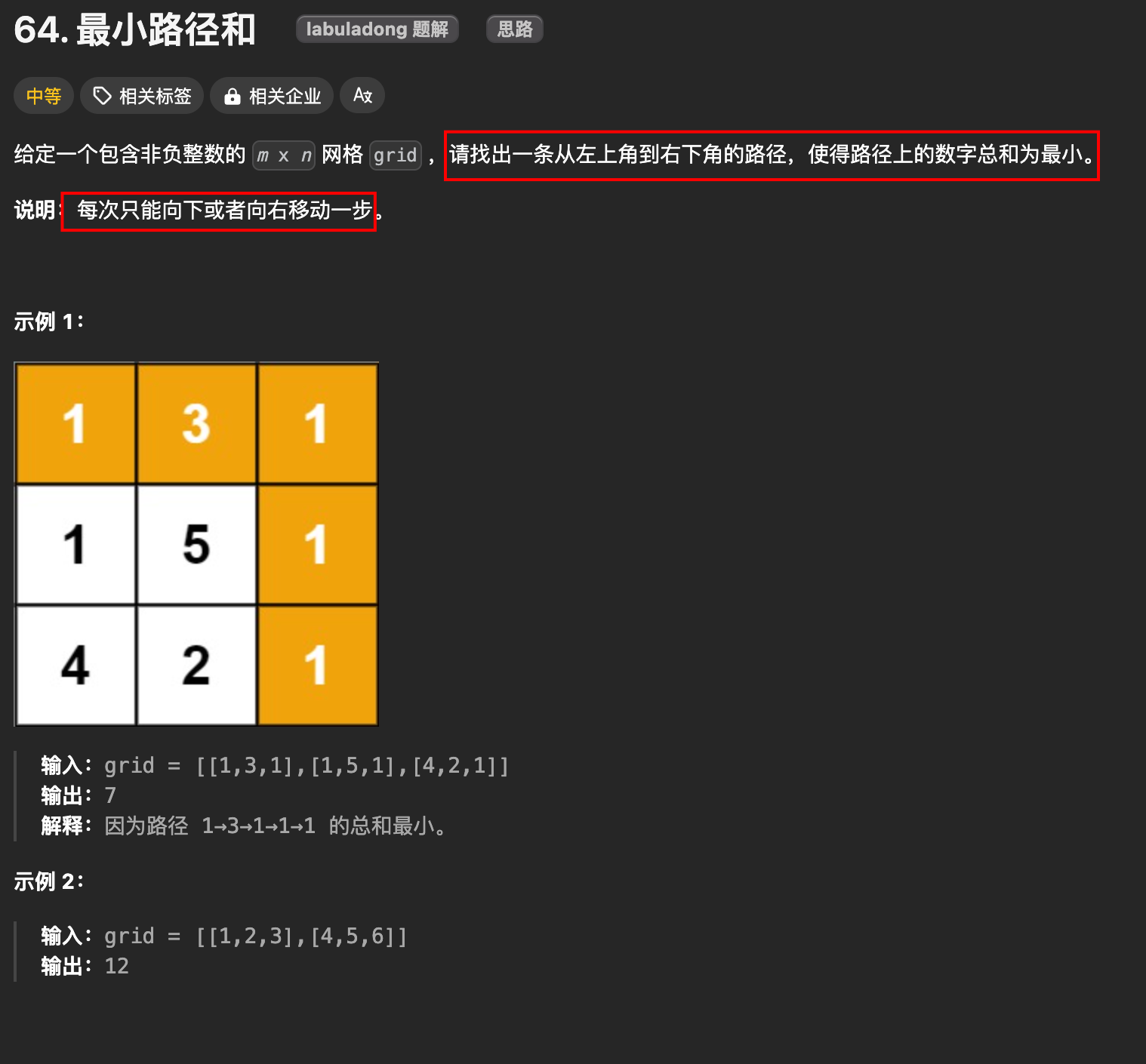
2. 分析
一般来说,让你在二维矩阵中求最优化问题(最大值或者最小值),肯定需要递归 + 备忘录,也就是动态规划技巧
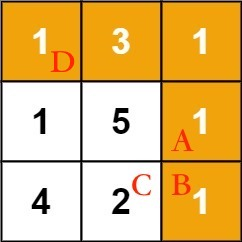
「从 D 走到 B 的最小路径和这个问题转化成了
- 从
D走到A的最小路径和 - 从
D走到C的最小路径和 这两个问题
2.1. 状态转移方法定义
// 从左上角位置 `(0, 0)` 走到位置 `(i, j)` 的最小路径和为 `dp(grid, i, j)`
var dp = function(grid, i, j) {}
2.2. 所以这个题的框架代码为
var minPathSum = function(grid) {
var m = grid.length;
var n = grid[0].length;
// 计算从左上角走到右下角的最小路径和
return dp(grid, m - 1, n - 1);
};
3. base Case 分析
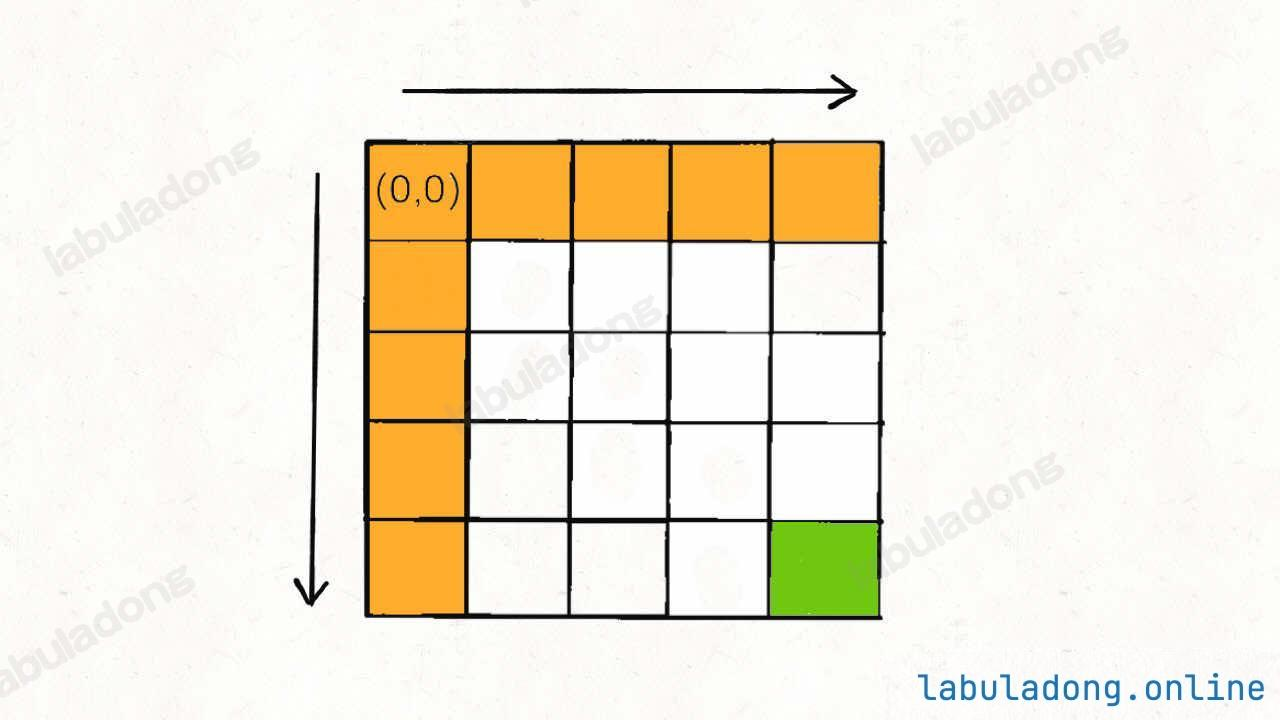
4. 自顶向下动态规划解法:会超时
var minPathSum = function (grid) {
var m = grid.length;
var n = grid[0].length;
// 计算从左上角走到右下角的最小路径和
return dp(grid, m - 1, n - 1);
function dp(grid, i, j) {
// base case:如果没有格子,取最左边和最上边的格子
if (i == 0 && j == 0) {
return grid[0][0];
}
// 如果索引出界,返回一个很大的值,
// 保证在取 min 的时候不会被取到
if (i < 0 || j < 0) {
return Number.MAX_VALUE;
}
return (
Math.min(
dp(grid, i - 1, j), // 左边的格子
dp(grid, i, j - 1), // 上边的格子
) + grid[i][j] // 当前格子的值
);
}
};
5. 自顶向下动态规划解法:使用备忘录优化
var minPathSum = function (grid) {
var m = grid.length;
var n = grid[0].length;
let memo = new Array(m).fill(-1).map(() => new Array(n).fill(-1));
// 计算从左上角走到右下角的最小路径和
return dp(grid, m - 1, n - 1);
function dp(grid, i, j) {
// base case:如果没有格子,取最左边和最上边的格子
if (i == 0 && j == 0) {
return grid[0][0];
}
// 如果索引出界,返回一个很大的值,
// 保证在取 min 的时候不会被取到
if (i < 0 || j < 0) {
return Number.MAX_VALUE;
}
// 如果计算过这个状态,就不要重复计算
if (memo[i][j] != -1) {
return memo[i][j];
}
return (memo[i][j] =
Math.min(
dp(grid, i - 1, j), // 左边的格子
dp(grid, i, j - 1), // 上边的格子
) + grid[i][j]); // 当前格子的值
}
};
6. 自底向上的迭代解法
var minPathSum = function (grid) {
var m = grid.length;
var n = grid[0].length;
let memo = new Array(m).fill(-1).map(() => new Array(n).fill(-1));
// 计算从左上角走到右下角的最小路径和
return dp(grid, m - 1, n - 1);
function dp(grid, i, j) {
// base case:如果没有格子,取最左边和最上边的格子
if (i == 0 && j == 0) {
return grid[0][0];
}
// 如果索引出界,返回一个很大的值,
// 保证在取 min 的时候不会被取到
if (i < 0 || j < 0) {
return Number.MAX_VALUE;
}
// 如果计算过这个状态,就不要重复计算
if (memo[i][j] != -1) {
return memo[i][j];
}
return (memo[i][j] =
Math.min(
dp(grid, i - 1, j), // 左边的格子
dp(grid, i, j - 1), // 上边的格子
) + grid[i][j]); // 当前格子的值
}
};