区间问题
#leetcode #2024/08/18 #算法/区间问题 #算法/双指针
目录
1. 区间问题解题思路
所谓区间问题,就是线段问题,让你合并所有线段、找出线段的交集等等。主要有两个技巧:
- 排序
- 先按照起点升序排序,
- 若起点相同,则按照终点降序排序。
- 画图。就是说不要偷懒,勤动手,两个区间的相对位置到底有几种可能,不同的相对位置我们的代码应该怎么去处理
2. LeetCode 1288:删除被覆盖区间
2.1. 题目
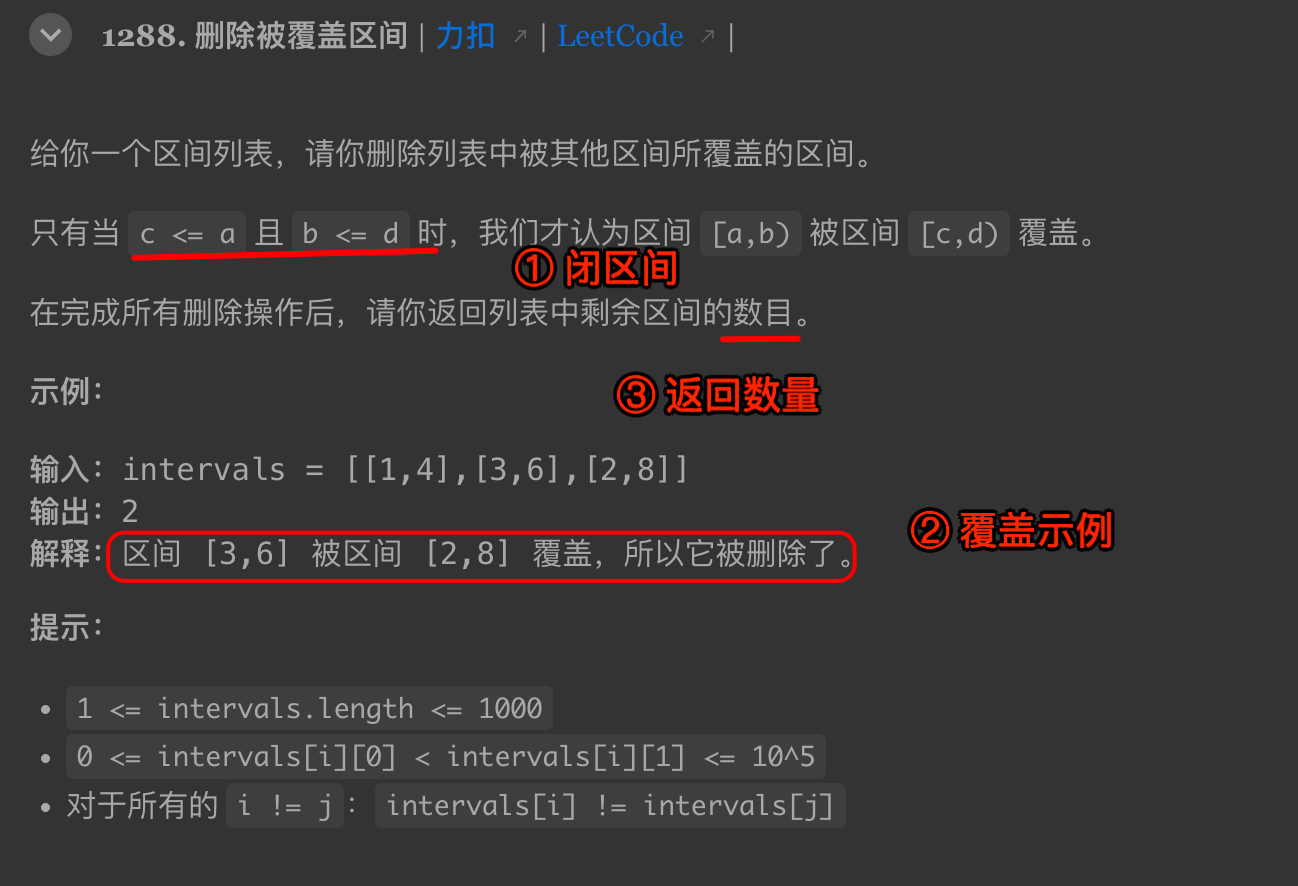
2.2. 思路
先排序,如下图
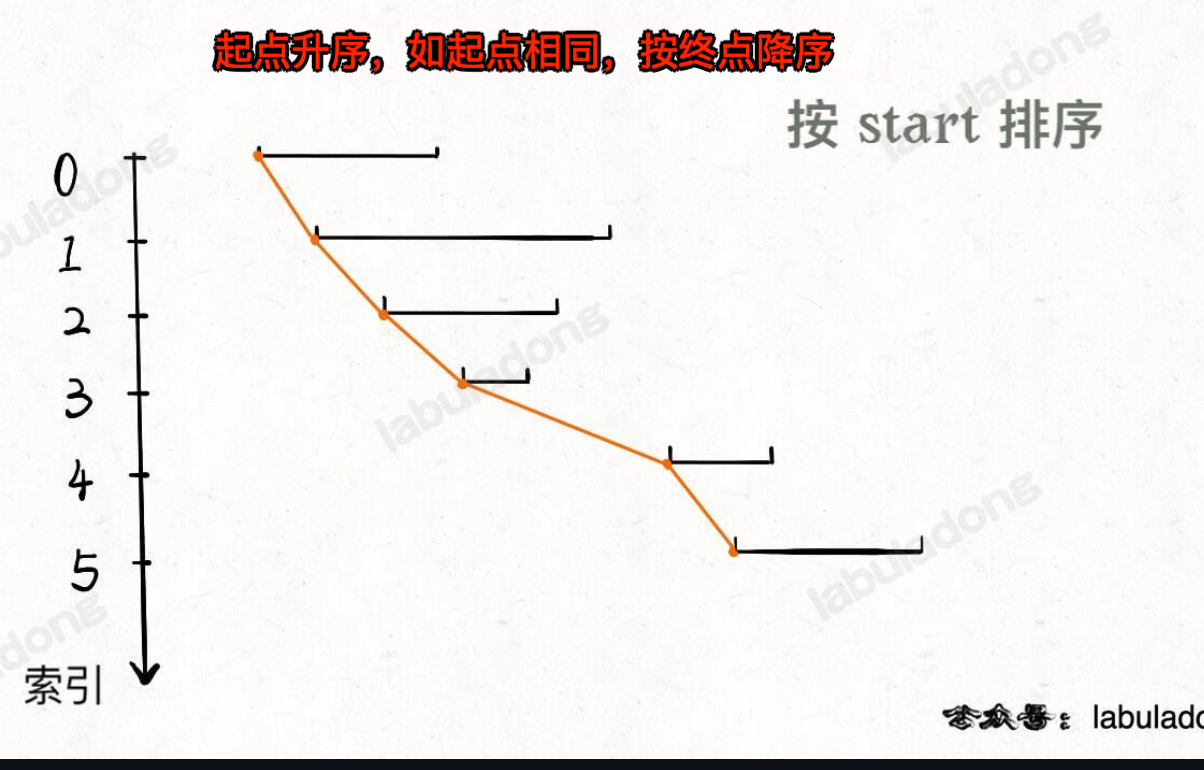
排完序后,只有下面三种情况
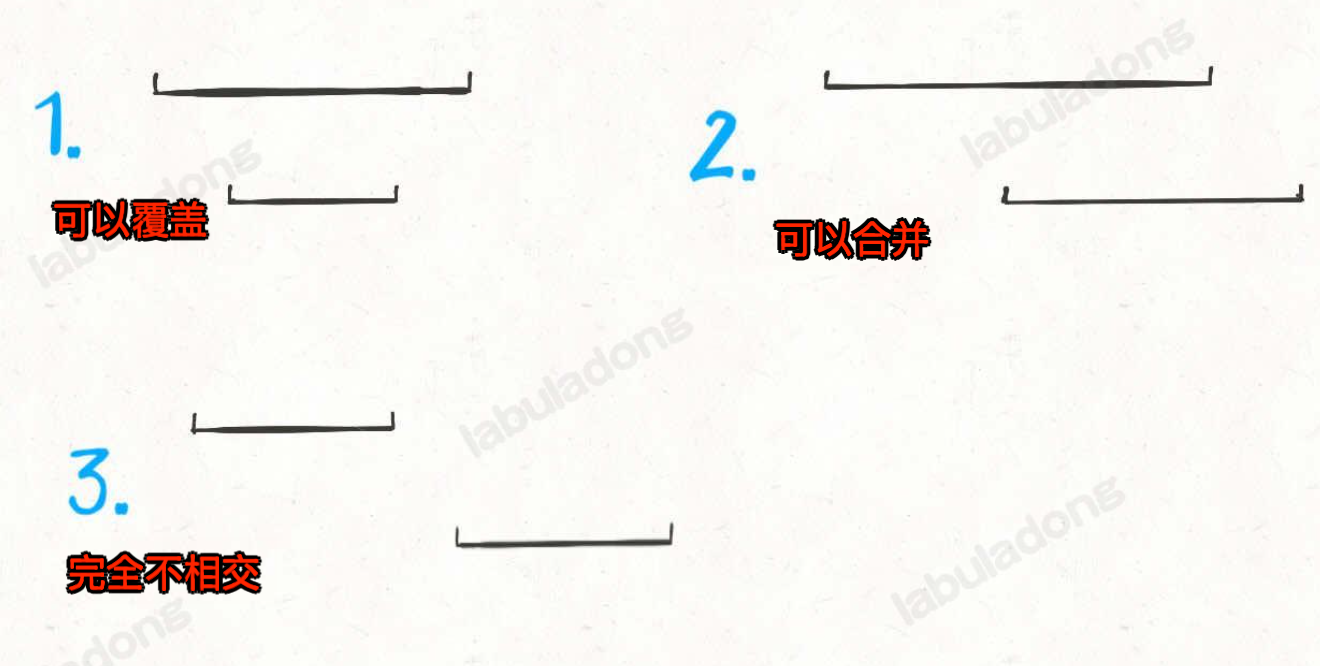
算法的关键点:
- 排序策略:按起始位置升序,相同起始位置时按结束位置降序。这确保了在处理重叠时的正确性。
- 三种情况的处理,下面三种情况涵盖了所有可能的区间关系
- 完全覆盖
- 可合并
- 完全不相交
- 遍历时使用了双指针,根据上面三种情况更新双指针
- 记住,返回的剩余的区间数
2.3. 代码实现
/**
* @description 区间列表的删除:区间问题
* @param {number[][]} intervals
* @return {number}
*/
var removeCoveredIntervals = function (intervals) {
let res = 0;
// ① 按照区间的起始位置排序,升序排序,如果起始位置相同,则按照结束位置降序排序
intervals.sort((a, b) => a[0] - b[0] || b[1] - a[1]);
// ② 初始化左指针,右指针,
// 左指针指向第一个区间的起始位置
// 右指针指向第一个区间的结束位置
let left = intervals[0][0];
let right = intervals[0][1];
// ③ 遍历区间数组
for (let i = 1; i < intervals.length; i++) {
let currInterval = intervals[i];
// 情况一:有重叠
if (left <= currInterval[0] && right >= currInterval[1]) {
res++;
}
// 情况二:可以合并
if (right < currInterval[1]) {
left = currInterval[0];
right = currInterval[1];
}
// 情况三:完全不相交
if (right < currInterval[0]) {
left = currInterval[0];
right = currInterval[1];
}
}
// 返回结果:区间列表的删除,即总区间数减去可以删除的区间数
// ::::题设中需要返回【剩余区间的数目】
return intervals.length - res;
};
2.4. 复杂度分析
时间复杂度分析:
- 排序:使用了 JavaScript 的内置排序方法,时间复杂度为
O(n log n),其中 n 是区间的数量。 - 遍历区间:一次线性遍历,时间复杂度为
O(n)。 - 总的时间复杂度:O(n log n) + O(n) =
O(n log n),主要由排序步骤决定。
空间复杂度分析:
- 排序:JavaScript 的排序算法通常使用额外的 O(log n) 到 O(n) 的空间。
- 其他变量(left, right, res):使用常数额外空间。
- 总的空间复杂度:
O(log n) 到 O(n),==主要取决于排序算法的实现==。
2.5. 错误记录
[!danger] 关于区间排序,一直觉得是 sort 里面嵌套 sort,其实不是,一个 sort 回调即可
arr.sort((a, b) => {
if (a[0] == b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
// 简写
arr.sort((a, b) => a[0] - b[0] || b[1] - a[1]);
3. 示例二:区间合并问题
4. 示例三:区间列表的交集
4.1. 题目
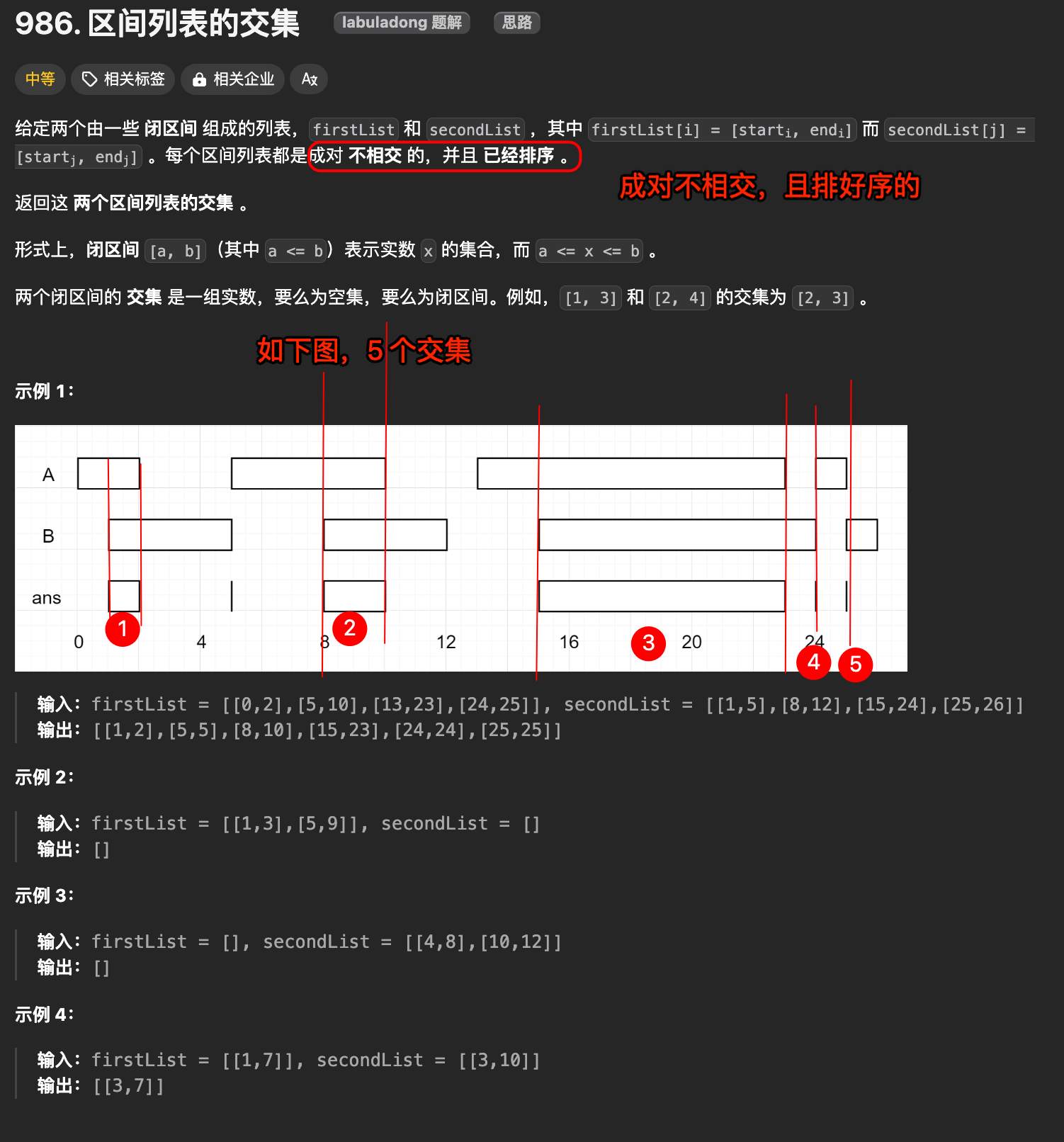
https://leetcode.cn/problems/interval-list-intersections/description/
4.2. 思路
- 我们用
[a1, a2]和[b1, b2]表示在A和B中的两个区间,- 如果这两个区间有交集,需满足
b2 >= a1 && a2 >= b1,分下面四种情况: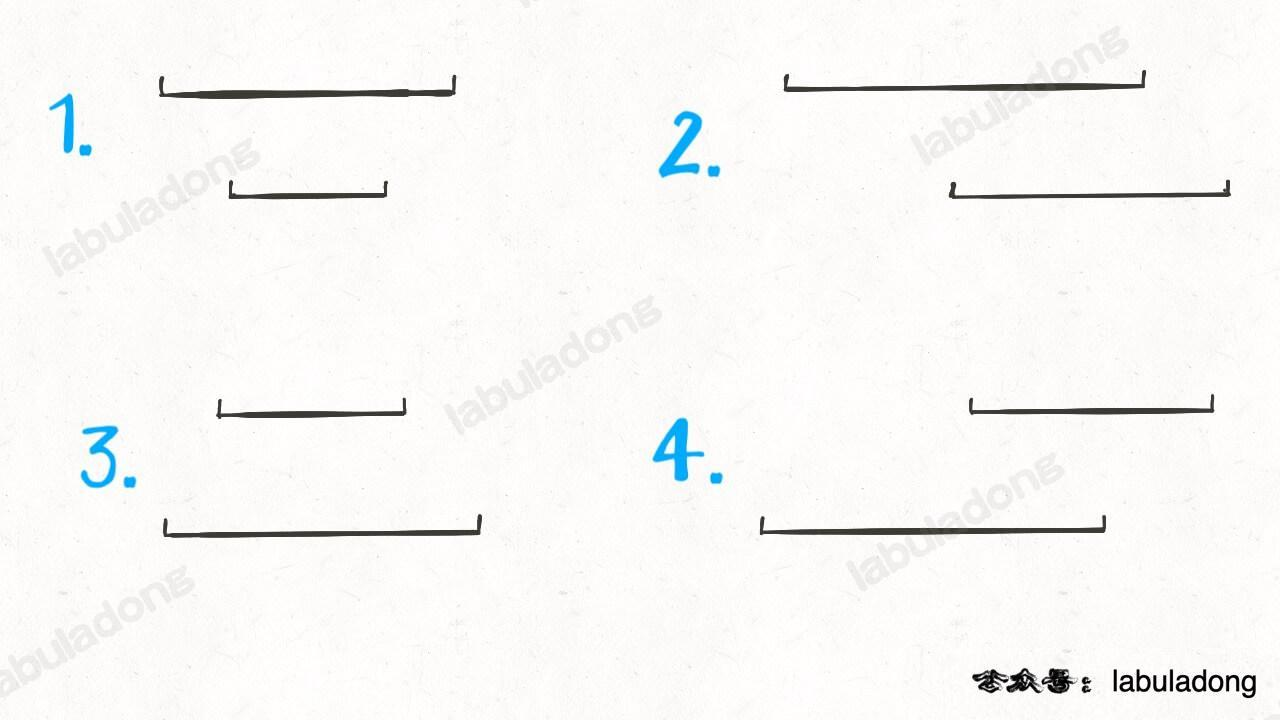
- 根据上图可以发现规律,假设交集区间是
[c1, c2]- 那么
c1 = max(a1, b1), c2 = min(a2, b2),如下图 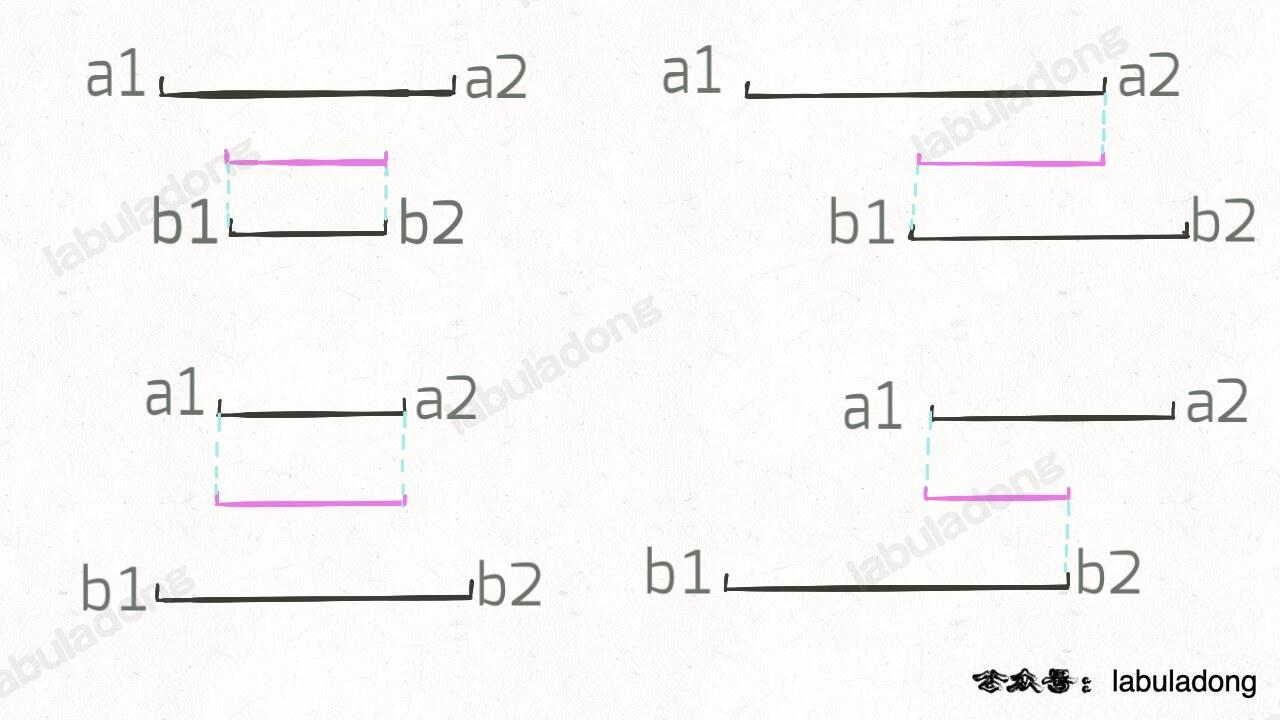
- 那么
- 如果这两个区间有交集,需满足
结合动图看看:

4.3. 代码实现
/**
* @description 区间列表的交集
* @param {number[][]} firstList
* @param {number[][]} secondList
* @return {number[][]}
*/
var intervalIntersection = function (firstList, secondList) {
let res = [];
// 双指针
let i = 0,
j = 0;
while (i < firstList.length && j < secondList.length) {
let a1 = firstList[i][0],
a2 = firstList[i][1];
let b1 = secondList[j][0],
b2 = secondList[j][1];
// ① 交集存在的情况:
// 即 b 区间的起始位置小于等于 a 区间的结束位置
// 并且 a 区间的起始位置小于等于 b 区间的结束位置
if (b2 >= a1 && a2 >= b1) {
res.push([Math.max(a1, b1), Math.min(a2, b2)]);
}
// ② 更新指针
// 如果 a 区间的结束位置小于 b 区间的结束位置,则 a 区间的指针向后移动
if (a2 < b2) {
i++;
// 如果 b 区间的结束位置小于 a 区间的结束位置,则 b 区间的指针向后移动
} else {
j++;
}
}
return res;
};
4.4. 复杂度分析
时间复杂度:
- 假设两个数组的长度都是 n。
- 算法遍历两个数组一次,每次循环最多执行一次。
- 因此,时间复杂度是
O(n)。
空间复杂度:
- 结果数组 res:在最坏情况下(所有区间都有交集),可能需要存储 n 个交集区间。
- 其他变量使用常数额外空间。
- 总的空间复杂度:
O(n),主要由结果数组决定。
算法的优点(考虑到数组长度相同):
- 高效:时间复杂度 O(n) 是线性的,这是解决此问题的最优复杂度。
- 一次遍历:通过一次遍历就能找出所有交集。
- 无需排序:假设输入列表已经按区间起始时间排序。
关键点:
- 双指针技巧:使用两个指针同步遍历两个列表。
- 交集判断和指针移动策略保持不变。
总结: 考虑到两个输入数组长度相同,这个算法的性能特征更加明确。它以 O(n) 的时间复杂度和 O(n) 的空间复杂度高效地解决了问题,其中 n 是每个输入数组的长度。这个方法对于查找两个等长排序区间列表的交集是最优解。
4.5. 注意点
- 利用双指针 技巧
- 另外
a1 、a2 、b1、b2 、c1 、 c2这几个变量的关系一定要搞清楚,不然会出问题