地下城游戏

#算法/动态规划

目录

• 1. 题目
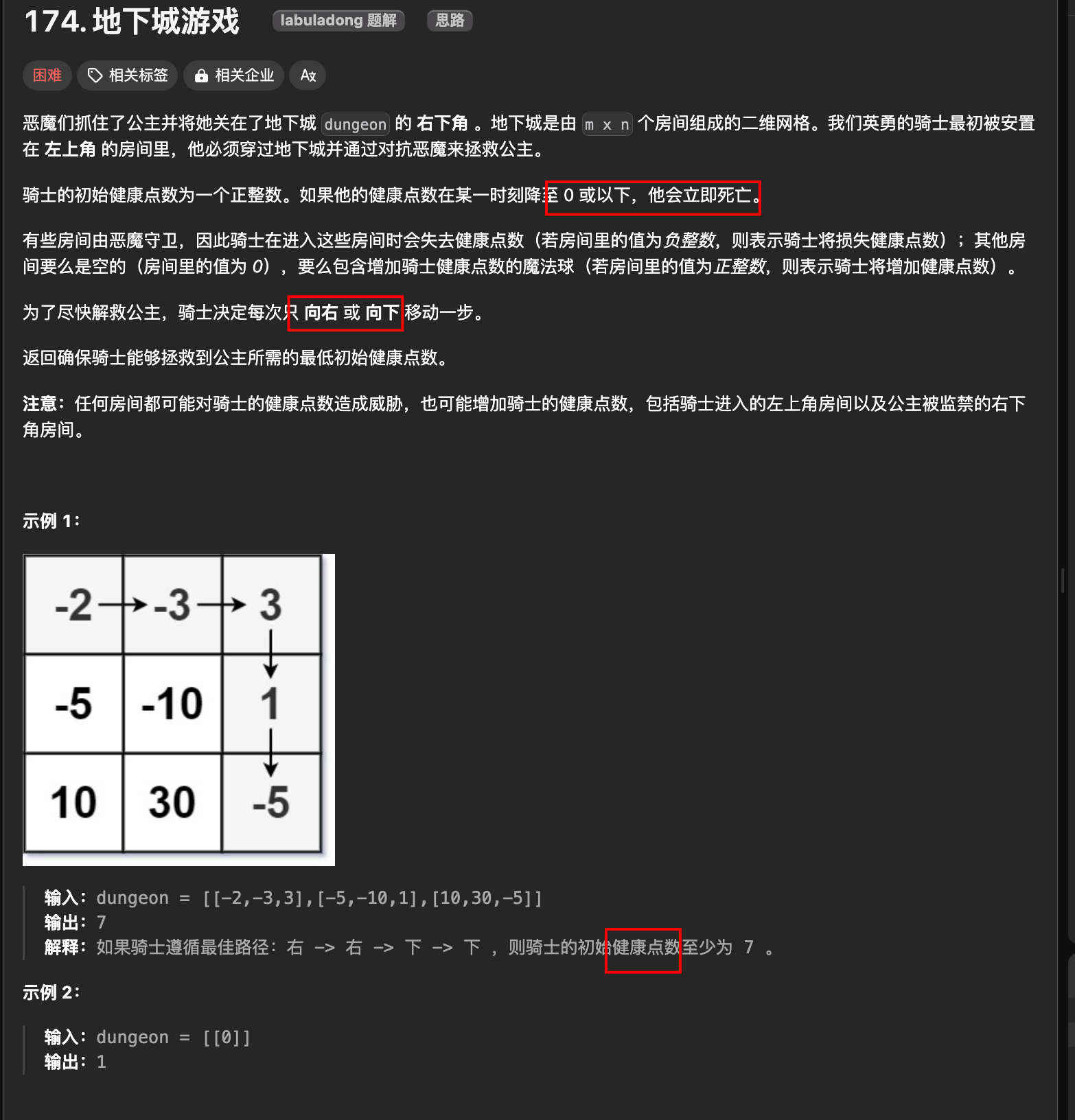
  • 1.1. 分析
• 2. dp 函数定义
• 3. 最终代码

1. 题目

1.1. 分析

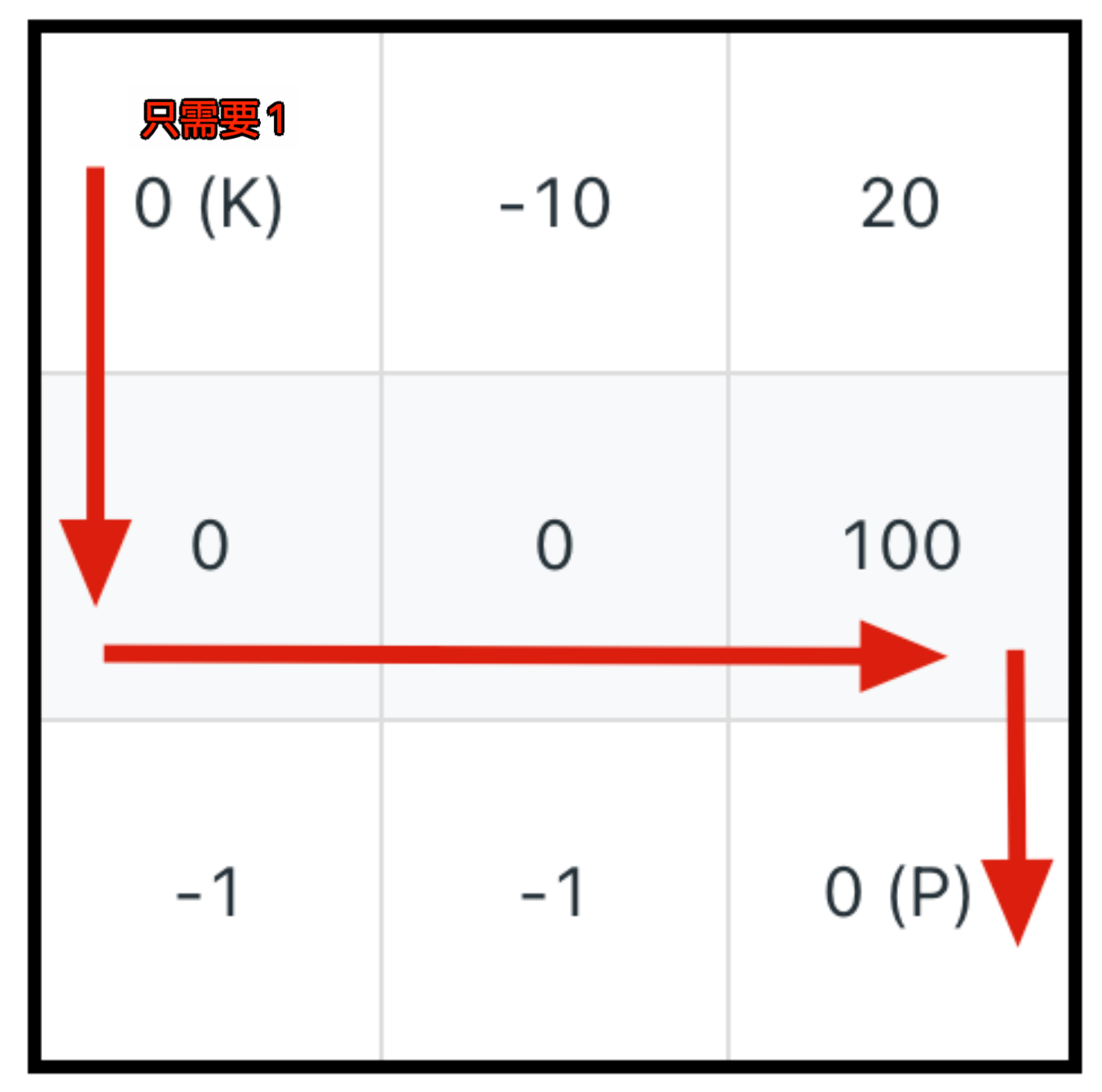
所以，关键不在于吃最多的血瓶，而是在于如何损失最少的生命值

2. dp 函数定义

从 grid[i][j] 到达终点（右下角）所需的最少生命值是 dp(grid, i, j)

从 A 到达右下角的最少生命值应该由下面两个值决定

• 从 B 到达右下角的最少生命值
• 从 C 到达右下角的最少生命值

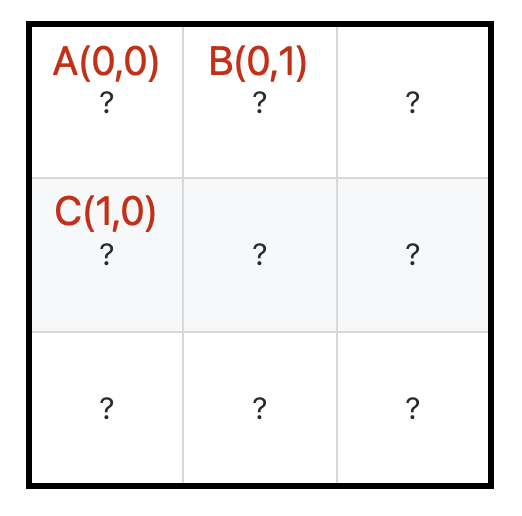
• B：从 (i, j+1) 出发，到达右下角，需要的最小初始血量
• C：从 (i+1, j) 出发，到达右下角，需要的最小初始血量
• 所以，选择 B 和 C 中的最小值，即 min(B,C)
  • 假设 B：dp(0, 1) = 5, C：dp(1, 0) = 4，那么可以肯定要从 A 走向 C，因为 4 小于 5 嘛
    • 假设 A = 1  
      • 既然知道下一步要往 C 走，且 dp(1, 0) = 4 意味着走到 grid[1][0] 的时候至少要有 4 点生命值，
      • 那么就可以确定骑士出现在 A 点时需要 4 - 1 = 3 点初始生命值
    • 那如果 A = 10 的值为 10，落地就能捡到一个大血瓶，超出了后续需求，4 - 10 = -6 意味着骑士的初始生命值为负数，
      • 这显然不可以，骑士的生命值小于 1 就挂了，所以这种情况下骑士的初始生命值应该是 1。

所以状态转移方程

int res = min(
    dp(i + 1, j),
    dp(i, j + 1)
) - grid[i][j];

dp(i, j) = res <= 0 ? 1 : res;

3. 最终代码

var calculateMinimumHP = function (grid) {
  const m = grid.length;
  const n = grid[0].length;
  // 备忘录中都初始化为 -1
  const memo = new Array(m).fill(0).map(() => new Array(n).fill(-1));
  return dp(grid, 0, 0, memo);
};

// 定义：从 (i, j) 到达右下角，需要的初始血量至少是多少
var dp = function (grid, i, j, memo) {
  const m = grid.length;
  const n = grid[0].length;
  // base case
  if (i == m - 1 && j == n - 1) {
    return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
  }
  if (i == m || j == n) {
    return Number.MAX_SAFE_INTEGER;
  }
  // 避免重复计算
  if (memo[i][j] != -1) {
    return memo[i][j];
  }
  // 状态转移逻辑
  // 解释：保证哪怕右边或者下边的血量为负，骑士的血量至少为 1
  const res =
    Math.min(
      dp(grid, i, j + 1, memo), // 从 (i, j+1) 出发，到达右下角，需要的最小初始血量
      dp(grid, i + 1, j, memo), // 从 (i+1, j) 出发，到达右下角，需要的最小初始血量
    ) - grid[i][j];
  memo[i][j] = res <= 0 ? 1 : res;
  return memo[i][j];
};